UHV输电暂态信号的动力学分析新方法

李 毅 吴政球 汪 沨 刘开培 陆佳政

（1.湖南大学电气与信息工程学院 长沙 410082 2.湖南省电力公司张家界电业局 张家界 427000 3.武汉大学电气工程学院 武汉 430072 4.湖南省电力试验研究院 长沙 410007）

1 引言

随着特高压电网在我国的运行与推广，电网的安全可靠运行已被提升到了一个重要的位置。一旦输电线路发生短路故障，对于保护装置能否正确识别故障类型并快速切除故障提出了更高的要求，由于特高压交流输电具有高电压、长距离等特点，线路分布参数不同于以往电压等级的电网，因此故障信息的正确识别也变得较为困难，如果对故障类型出现漏判或误判，将会导致电网故障范围的扩大，进而有可能冲击主网，引发骨架网络的瘫痪。电流差动保护原理简单，灵敏度高，具有天然的选线能力，然而由于特高压交流输电线路的分布电容较大，仅采用此方法进行识别往往会出现误判，因此通常结合检测故障行波的方法来识别故障，但是行波在向两侧传播的过程中，易于衰减畸变，还会叠加环境干扰信号。因此，正确快速地从干扰信号中提取微弱行波的故障信息对于识别故障类型具有重要意义。文献[1]利用Duffing振子信号检测技术来检测外界信号，成功实现了配电网单相接地故障的保护选线。文献[2]利用混沌理论检测接地故障，对支路电流采样所得干扰信号进行混沌化处理，提取了混沌源的分类特征。文献[3-9]均从动力学角度，利用混沌系统对微弱信号进行了检测，取得了很好的效果。由于输电线路的暂态信号表现出混沌特性，因此，可从动力学的角度去分析暂态信号的故障模式，本文在分析暂态过电流极值变化的基础之上，对故障信号进行相空间重构，并比较了不同故障模式下故障信号的混沌特征变化规律，同时，利用Duffing混沌系统在高压网络同样对弱信号具备良好检测能力的优点，将不同带噪故障信号输入到检测系统中，得到了所要检测信号的相轨迹图[10,11]，再对相轨迹图进行小波边缘检测，提取到不同故障类型下的故障特征量和指纹检测区。研究表明，本文所提动力学分析方法可行。

2 暂态故障模型的仿真与分析

2.1 1 000kV特高压线路故障的建模

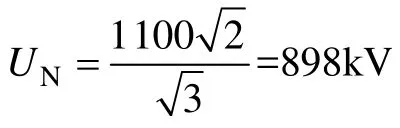
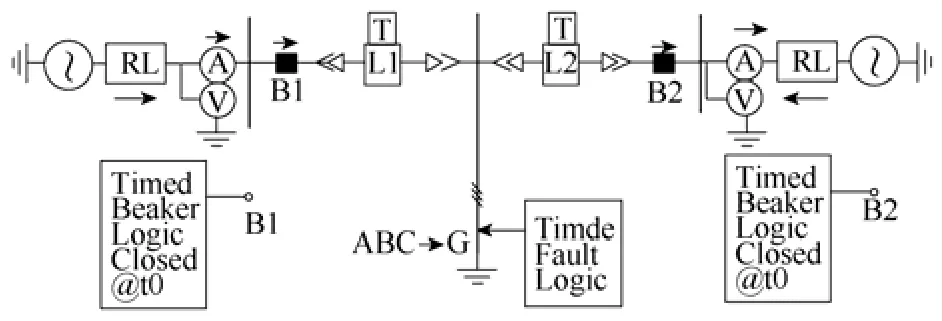
图1 1 000kV特高压线路故障仿真Fig.1 Fault simulation for 1 000kV UHV line

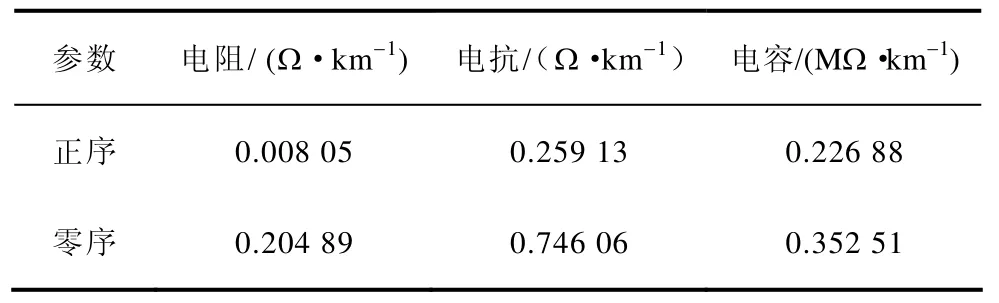
表1 输电线路主要参数Tab.1 Main parameters of transmission line

图2 输电线路杆塔模型Fig.2 Tower model for UHV transmission line

2.2 输电线路故障的仿真分析

下面以特高压交流输电线路作为研究对象，当发生三相对称性短路故障f(3)，三相非对称性故障（单相接地故障f(1)、双相短路故障f(1,1)、双相短路接地故障f(2)）时，考虑到线路两侧重合闸会产生单重或三重动作，下面将研究各种情况下故障相与非故障相中的暂态电流信号的特征变化，并利用动力学分析故障相电流信号的最大值im、分维数F、KE熵随接地电阻、相位差、故障点位置的变化特征[14,15]。

仿真计算得出，当发生单相（A相）接地故障，双端全相跳闸时，A相暂态信号的分维数为1.250 1，KE熵为0.002 1；而当发生单相（A相）接地故障，双端单相（A相）跳闸时，暂态信号的分维数为1.330 3，KE熵为0.000 8。结合表2可知，分维数大小规律为1.330 3＞1.293 0＞1.250 1＞1.178 4＞1.044 7，KE熵值大小规律为0.002 3＞0.002 1＞0.001 9＞0.001 0＞0.000 8。因此当发生单相故障时，双端跳单相情况下信号分维数较双端跳全相要大，KE熵值则恰恰相反。此外，由于不同故障类型具备不同的分维数F值和KE值，因此利用该特征量可以对故障类型进行区分。据统计， 70%以上的特高压线路故障多因单相接地故障所致，因此下面着重分析单相接地故障类型，并重点讨论故障点位置、接地阻抗及双端相角差对故障相中暂态电流信号的影响，并重点分析其动力学指数的变化规律。

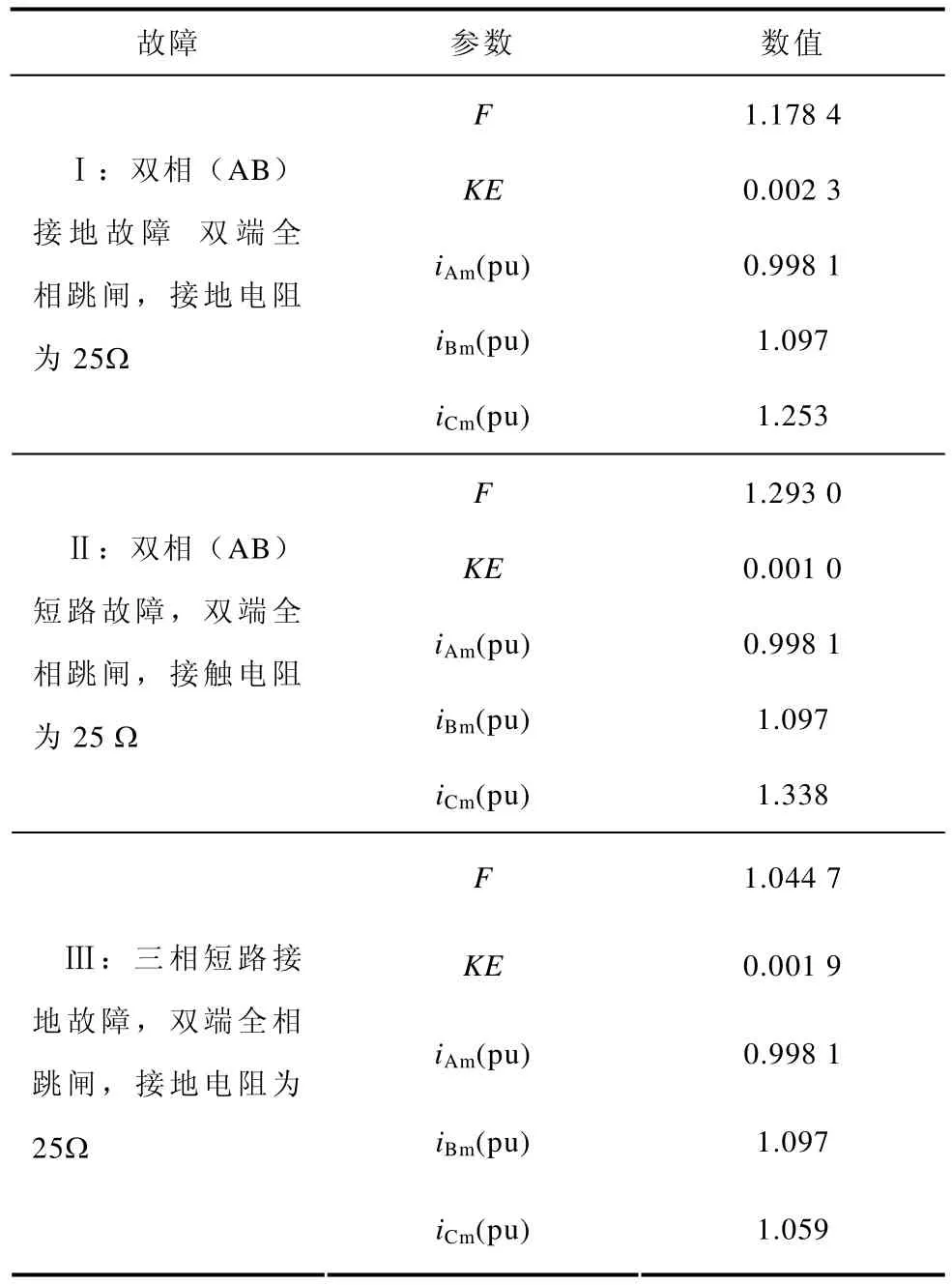
表2 不同故障模式下信号特征量的对比Tab.2 Comparison of signal characteristics in different failure modes

故障类型Ⅳ：单相（A相）接地故障，双端A相跳闸。当故障点位于L1=50km，接地阻抗Z分别为0、25、50、75、100、125、150、175、200Ω时，得到故障相中暂态信号的特征量随接地电阻大小的变化关系曲线如图3所示。

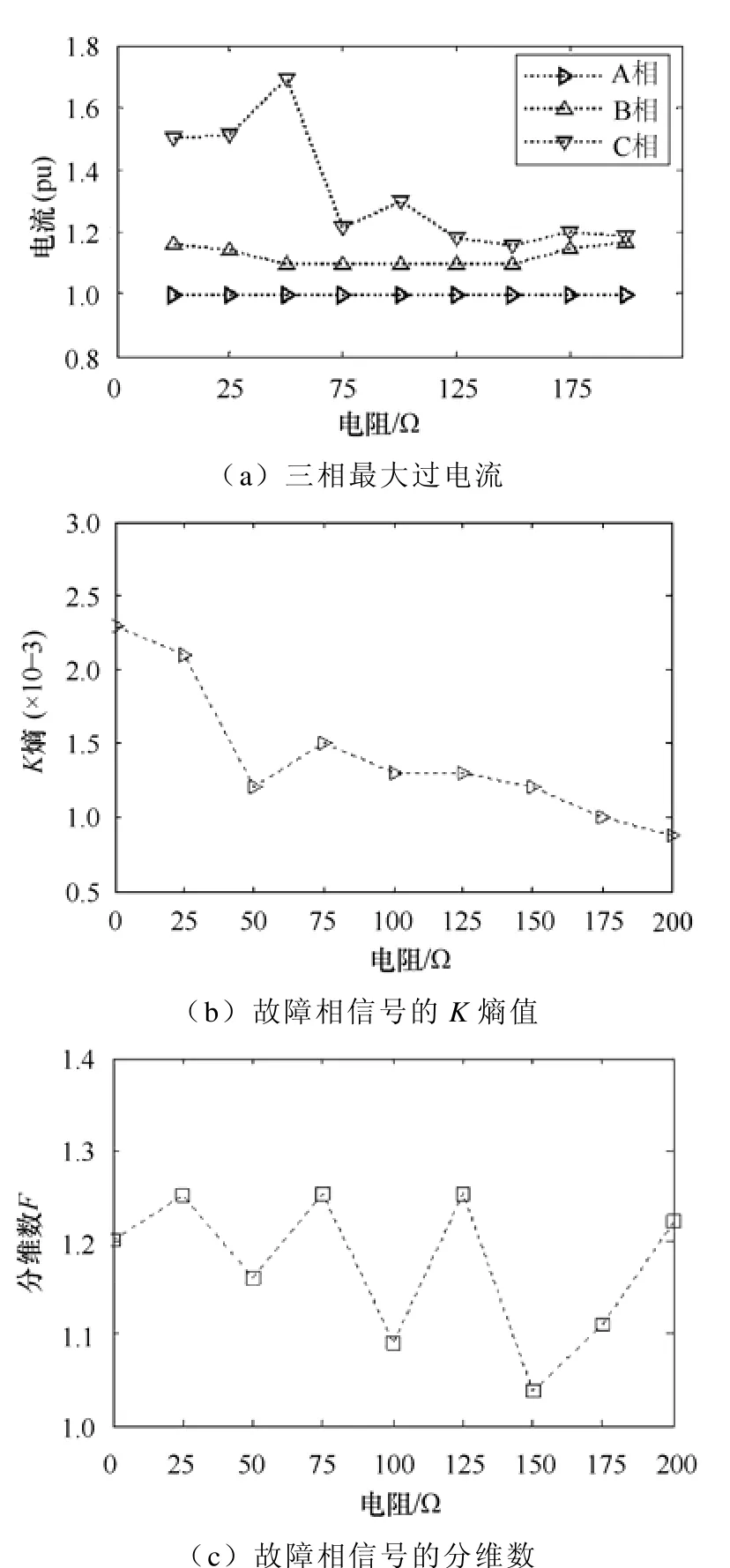
图3 故障相信号特征量与接地电阻之间的关系Fig.3 Relationship between signal feature of fault phase and grounding resistance

故障类型Ⅴ：单相（A相）接地故障，双端单相（A相）跳闸，接地电阻25Ω。当双端电源相角差分别为0°、30°、60°、90°、120°和150°时，得到故障相暂态信号与相位差之间的关系曲线如图4所示。

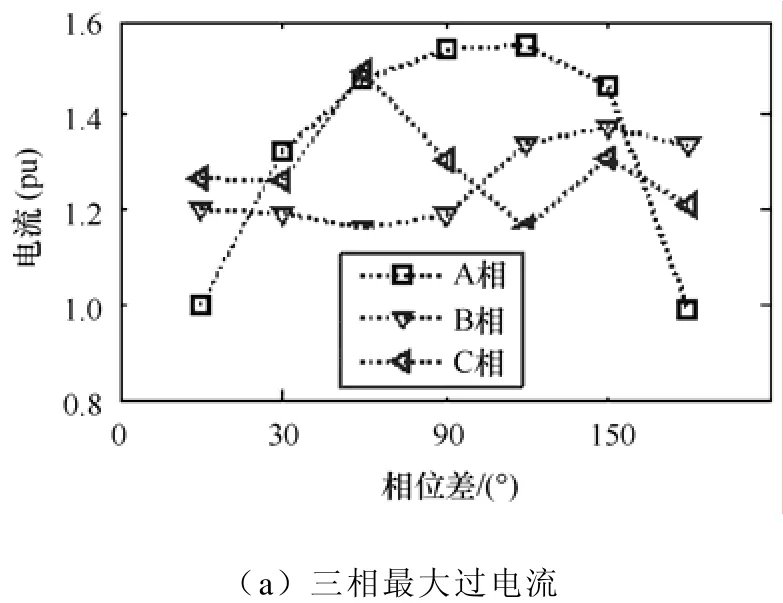
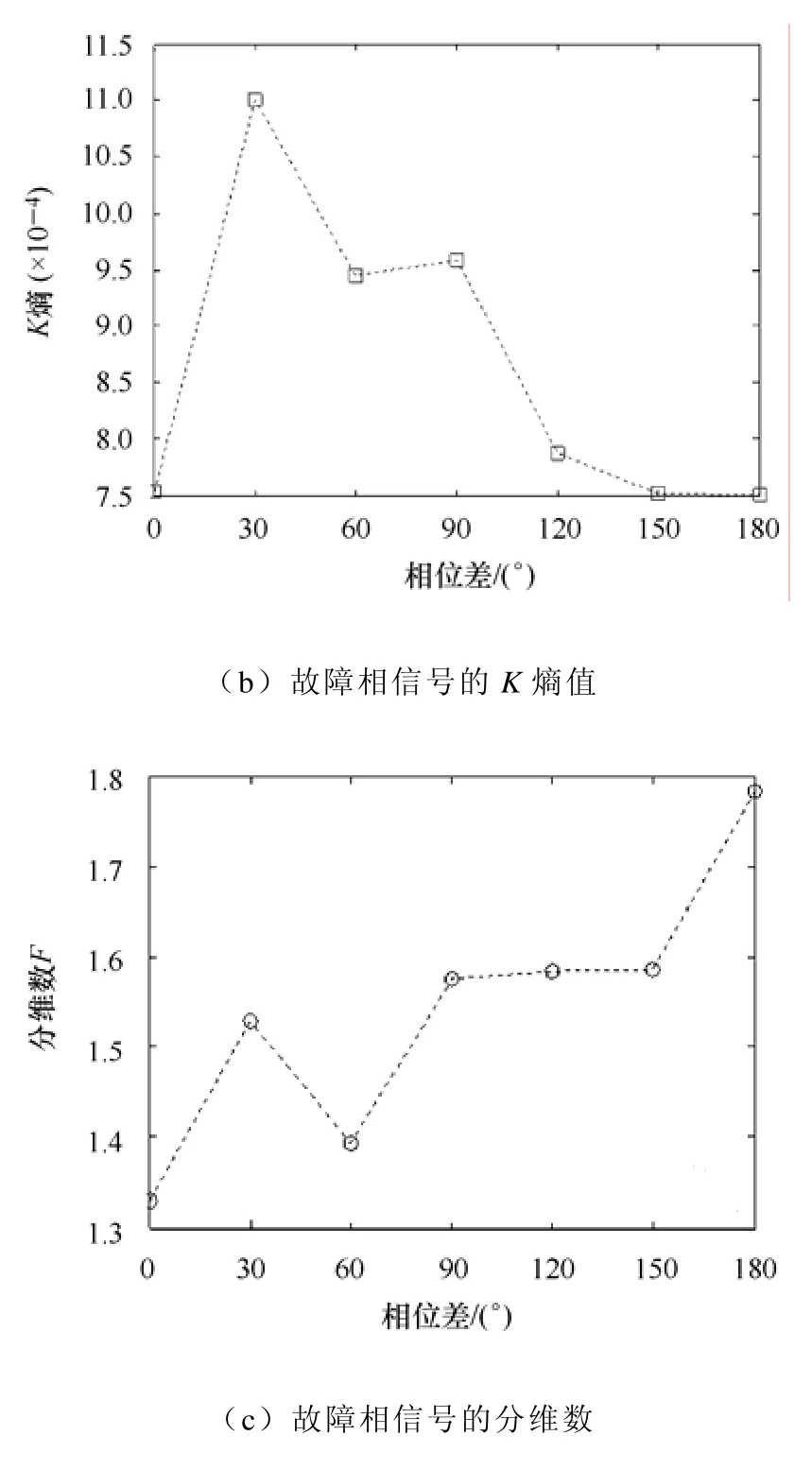
图4 故障相信号特征量与相角差之间的关系Fig.4 Relationship between signal feature of fault phase and phase angle difference

故障类型Ⅵ：单相（A）接地故障，双端单相（A）跳闸，接地电阻25Ω，电源相角0°。从左至右故障点依次设置在0、50、100、150、200、250、300、350、400km处时，得到故障相暂态信号与故障点位置之间的关系曲线如图5所示。

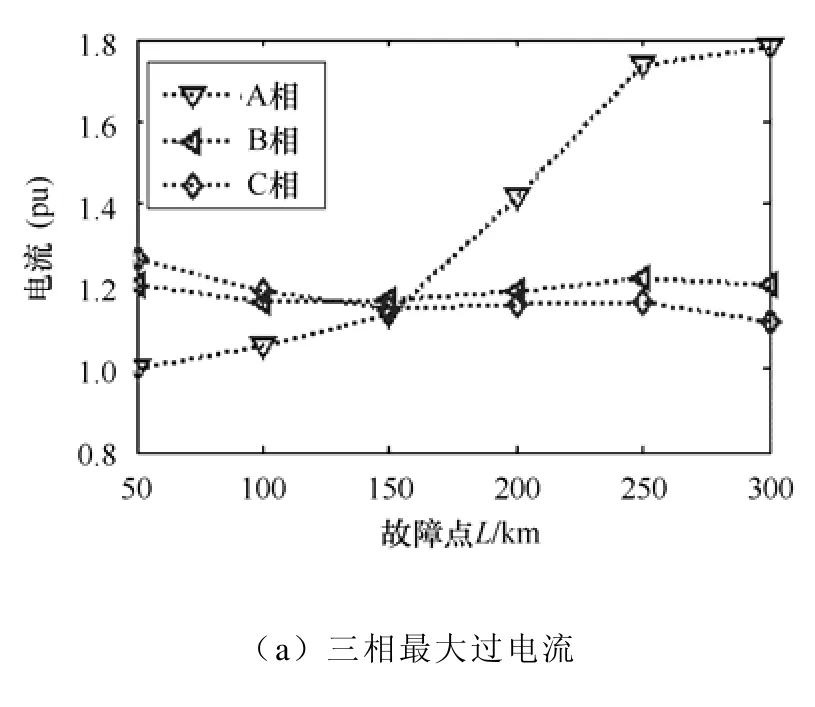
图5 故障相信号特征量与故障点位置之间的关系Fig.5 Relationship between signal feature of fault phase and location of fault point

通过分析不同故障类型下故障相中的过电流特征量变化规律，得到如下结论：

（1）当L1=50km处发生A相接地故障，双端全相跳闸时，为分析接地阻抗对A、B、C三相过电压的影响，通过对图3a分析，发现随着接地阻抗的增加，非故障相（B、C相）暂态电流信号变化微弱，而故障相（A相）中的暂态电流在接地电阻为50Ω时达到最大值，随后下降。通过对图3b中A相暂态信号的K熵值变化分析，发现随着接地阻抗的增加，暂态信号的K熵值变小，在接地阻抗为50Ω时，出现突降。表明A相过电流达到最大值时，暂态信号dK/dR比值变化剧烈，即此时暂态信号混沌性随阻抗变化较剧烈。分析图3c，发现该接地故障模式下，暂态信号的分维数分布域为1.036 8～1.252 2。

（2）当L1=50km处发生A相接地故障，接地电阻25Ω，双端单相（A相）跳闸，信号特征量与相位差大小二者之间的关系如图4所示，分析发现A相电流的最大值随相角差增加呈现倒“U”字型变化趋势。当相角差为120°时达到最大过电流1.55(pu)。另外此故障模式下，分维数随相角差的增加呈现递增趋势，而K熵值则在相角差大于30°后总体呈递减趋势。

（2）当L1=50km处发生A相接地故障，双端单相（A相）跳闸。信号特征量随故障点位置的变化关系如图5所示，发现随着故障点距离的增加，A相过电流增至1.783(pu)，B、C相则变化较小。此外，分维数随相角差呈递增趋势，大小介于1.430 3～1.894 6之间，K熵曲线呈“U”变化。

2.3 故障暂态信号的相图比较

下面就以下5种最可能出现的故障模式进行相图分析，先假定电源双端相角差δ均为30°，接地阻抗为25Ω，故障点均位于线路左侧的1/4位置处。

单相（A相）接地故障，双端单相（A）跳闸，这一过程，简称为G11。

单相（A相）接地故障，双端三相跳闸，简称为G13。

双相接地（AB相）故障，双端全相跳闸，简称为G23。

双相短路（AB相）故障，双端全相跳闸，简称为G2′3。

三相短路接地故障，双端全相跳闸，简称G33。

图6为故障信号在经相空间重构后所得相图的比较，其中F1代表参量X、X(t+τ)、dX/dt构成的三维相图，F2代表X与X(t+τ)构成的二维相图，F3代表X与dX/dt构成的二维相图。通过对图6a～图6e比较分析，发现不同故障模式下检测到的暂态电流信号经相空间重构之后，具备不同的相点分布特征，因此，可以利用该特性来识别特高压线路故障。

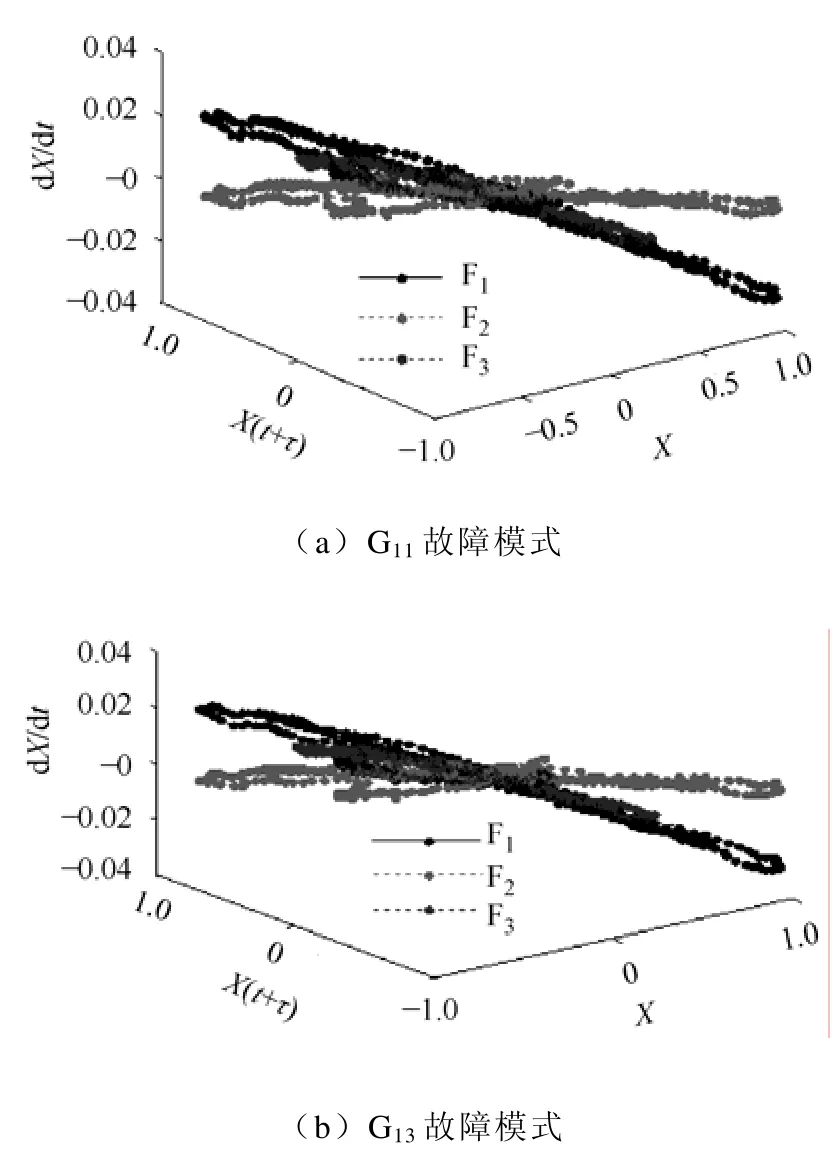
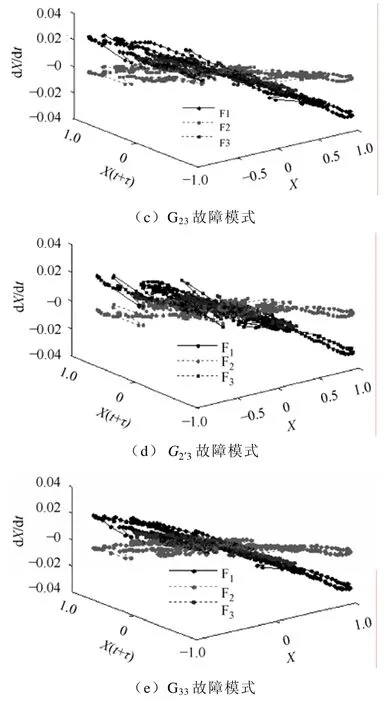
图6 各故障下A相暂态信号的相图比较Fig.6 Comparison for phase A diagram of transient signal under various fault models

2.4 暂态信号的混沌控制分析

2.4.1 Duffing混沌控制电路

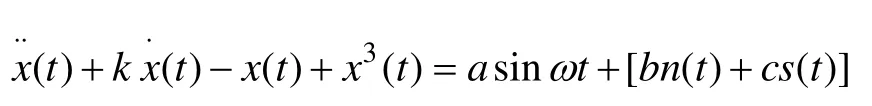
首先取ω=0.5rad/s，调节阻尼比k，当仅有策动力作用时，发现k=0.4～0.826时信号的相轨迹呈现混沌态；当k=0.826时临界混沌轨迹图如图7a所示；当k=0.826 1时，相轨迹将从临界混沌态进入到稳定周期状态，如图7b所示。因此，检测前先设定k=0.826 1，将相轨迹纳入到周期状态作为检测初态，再将带噪的故障信息输入到混沌检测系统中，其中x˙(t)表示x(t)的对时间t的一阶导数。

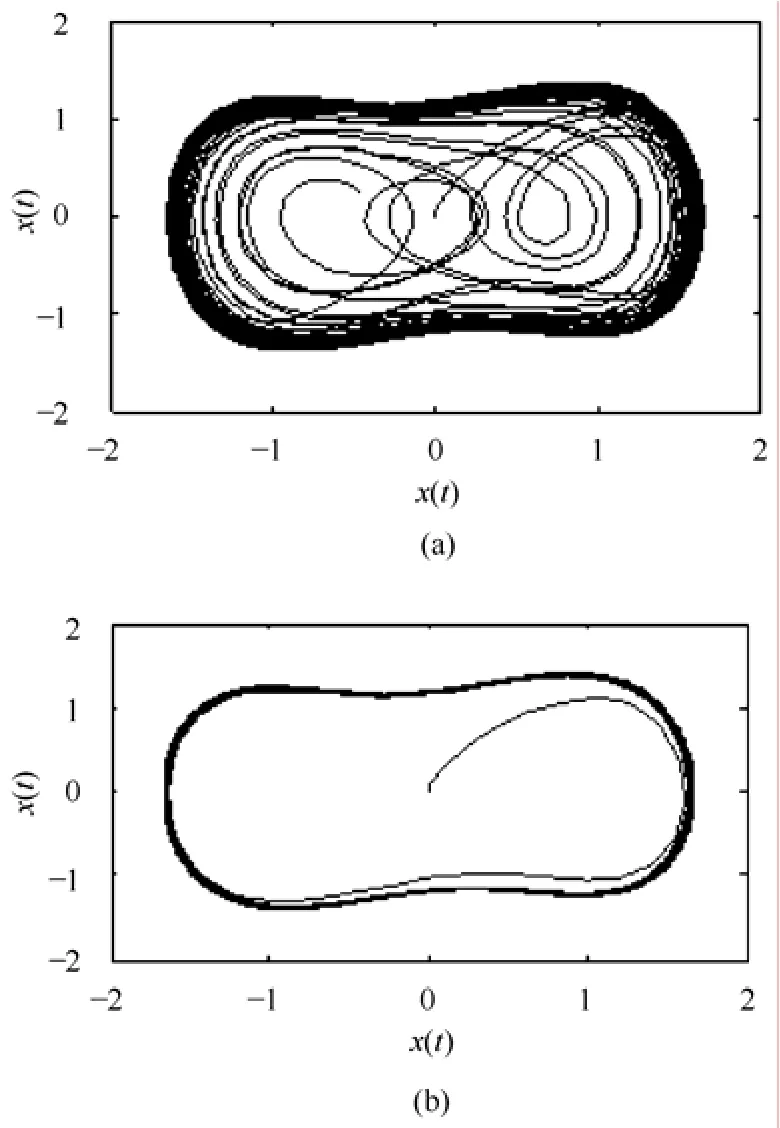
图7 临界相轨迹图Fig.7 Critical phase trajectory

对于处于稳定周期态的混沌系统而言，由于系统对于频率接近系统运动频率的弱信号具有极度敏感性，而对其他非同频的干扰信号具有良好的抗干扰能力。因此可以利用Duffing混沌控制电路来检测带噪的故障信号，检测电路如图8所示。

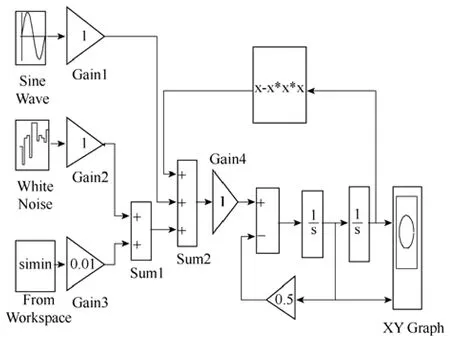
图8 带噪故障信号的混沌检测电路Fig.8 Chaotic detection circuit for noisy fault signal

下面分别对G11、G13、G23、G2′3、G33故障模式下故障相(A相)电流进行混沌检测仿真比较，得到相轨迹图形如图9所示。

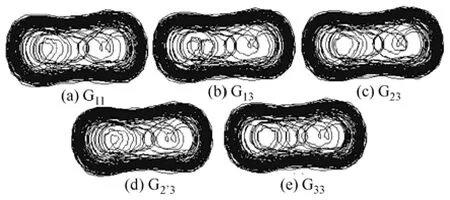
图9 混沌系统检测到的相轨迹Fig.9 Phase trajectory detected by chaotic system

2.4.2 混沌相图的小波边缘检测

为便于识别不同故障类型，减小图形存储空间，对图9中5种故障模式的相轨迹进行小波边缘检测。比较发现，带噪的故障信号在经检测系统去噪之后，得到了较为清晰的相轨迹图（图9），再对图9进行小波边缘检测后，得到指纹图10，利用图10中的指纹信息（红色方框区域）能较好地将各子图中所包含的故障信息提取出来，进而便于故障类型的识别。

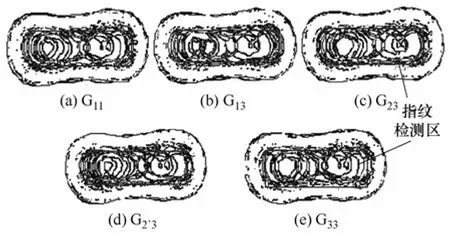
图10 小波边缘检测后的相轨迹比较Fig.10 Comparison of phase trajectory by wavelet edge detection

3 现场故障类型的识别

图11为某750kV输电线路模拟单相接地故障跳单相和三相接地故障跳三相时，所检测到的电流信号。现场采用宽频带脉冲传感器进行故障信息的采集，采样频率为20MHz。为进一步验证本文所提出的混沌检测系统对环境干扰的抗噪性能，对现场采集到的录波数据（见图11）中加入白噪声，使信噪比低于-15dB，再将其送入Duffing检测系统中，得到带噪信号检测后的混沌相图，再对相图进行小波边缘检测[1-4]。混沌检测结果如图12所示，分析发现单相与三相故障模式具备不同的混沌指纹区，这与仿真结果图10a、图10e中的指纹区相吻合，识别结果分别为G11、G33故障模式。实际运行中存在很多的环境干扰，如电磁干扰，包括周期性窄带、脉冲干扰、白噪声等，由于Duffing检测系统具备选频特性，能对窄带信号、白噪声进行很好的抗干扰，而对于脉冲宽频信号抗干扰能力则较弱，因此进入Duffing检测系统之前须对脉冲干扰进行预处理，本文在对Duffing系统做现场验证时，并没有对脉冲干扰进行预处理，发现图12相图外区域中存在许多的散点，均与此有关，但其并没影响到故障模式的指纹检测区（方框区域）。因此，当脉冲型干扰很小的，其影响可以克服，现场验证时也证明了这点。

图11 现场故障信号的识别Fig.11 Fault signals dectected at scene

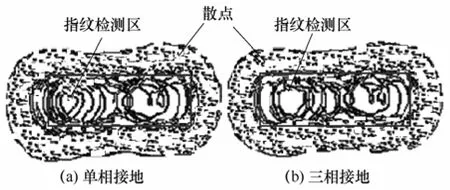
图12 现场故障信号的识别Fig.12 Recognition of fault signals detected at scene

4 结论

将动力学理论与混沌检测系统相结合，对特高压输电线路故障模式进行了仿真研究和现场检验。得出不同故障类型的相图具备不同的相点分布特征，利用该特征可以很方便地对故障类型进行识别。同时文中就实际采集故障信号时可能会出现的环境干扰影响做了分析，通过现场模拟验证了Duffing检测电路具备较好的抗干扰和识别能力，适用于对信噪比较小的故障信息进行故障模式的识别。此外，从存储空间节约，提高识别快速性的角度出发，提出了对经系统检测后的相轨迹图形进行小波边缘检测，利用比较相图中的指纹区进行识别的新方法。

[1] 尚秋峰,杨以涵,李士林,等.Duffing振子信号检测方法用于配电网单相故障接地保护[J].电力系统自动化,2004,28(13): 64-67.Shang Qiufeng,Yang Yihan,Li Shilin,et al.Duffing oscillator signal detection method applies to the single-phase to ground fault protection in distribution systems[J].Automation of Electrie Power Systems,2004,28(13): 64-67.

[2] 李冬辉,贾巍.用混沌理论检测直流供电系统接地故障[J].高电压技术,2005,31(11): 79 -82.Li Donghui,Jia Wei.application of chaos theory in grounding fault detection of DC power supply system[J].High Voltage Engineering,2005,31(11):79-82.

[3] Wang Guanyu,Chen Dajun,Lin Jianya,et al.The application of chaotic oscillators to weak signal detection[J].IEEE Transactions on Industrial Electronics,1999,46(2): 442-444.

[4] Jimenez-Triana,A Tang,W K S.Chaos control in duffing system using impulsive parametric perturbations[J].IEEE Transactions on Circuits and Systems,2010,57(4): 305-306.

[5] Zhen Zhao,Fu Li,Wang Mingxing,et al.Intermittent-chaos-and-cepstrum-analysis-based early fault detection on shuttle valve of hydraulic tube tester[J].IEEE Transactions on Industrial Electronics,2009,59(7): 2764-2766.

[6] 杨红英,叶昊.基于混沌理论的动态系统故障检测研究与发展[J].自动化与仪器仪表,2007,01: 1-4.

[7] 王冠宇,陶国良.混沌振子在强噪声背景信号检测中的应用[J].仪器仪表学报,1997,18(2):209-212.

[8] 聂春燕,石要武.基于互相关检测和混沌理论的弱信号检测方法研究[J].仪器仪表学报,2001,22(1):32-35.

[9] 王永生,姜文志,赵建军,等.一种Duffing弱信号检测新方法及仿真研究[J].物理学报,2008,57(4):2053-2056.Wang Yongsheng,Jiang Wenzhi,Zhao Jianjun,et al.A new method of weak signal detection using Duffing oscillator and its simulation research[J].Acta Physica Sinica,2008,57(4): 2053-2056.

[10] 赵彤,李庆明,陈平.OLTC振动信号特征提取的动力学分析方法[J].电工技术学报,2007,22(1): 42-45.Zhao Tong,Li Qiongmin,Chen Ping.Dynamic analysis method for feature extraction of mechanical vibration signals of on-load tap changers[J].Transactions of China Electrotechnical Society,2007,22(1): 42-45.

[11] 舒印彪,张文亮.特高压输电若干关键技术研究[J].中国电机工程学报,2007,27(31): 1-6.Shu Yinbiao,Zhang Wenliang.Research of key technologies for UHV transmission[J].Proceedings of the CSEE ,2007,27(31): 1-6.

[12] 刘振亚.特高压电网[M].北京:中国经济出版社,2005.

[13] 柴济民,郑玉平.交流1 000 kV特高压输电线路距离保护特殊问题[J].电力系统自动化,2007,31(12):55-59.Chai Jiming,Zheng Yuping.Problems in the distance relay for 1 000 kV UHV AC transmission lines[J].Automation of Electric Power Systems,2007,31(12):55-59.

[14] 郭征,贺家李,王俊.特高压长线路单相自适应重合闸的新原理[J].高电压技术,2009,35(5):1005-1008.Guo Zheng,He Jiali.Wang Jun,Research of single-phase self-adaptive reclosure for UHV long transmission lines[J].High Voltage Engineering,2009,35(5): 1005-1008.

[15] 吕金虎,陆君安,陈士华.混沌时间序列分析及其应用[M].武汉: 武汉大学出版社,2002.