基于QuickBird卫星遥感影像的几何纠正方法对比

李卫国， 高 飞， 陈文玲

（1.石家庄经济学院 勘查技术学院，河北 石家庄 050031；2.合肥工业大学 土木与水利工程学院，安徽 合肥 230009；3.中国地质大学江城学院 地质科学与工程学部，湖北 武汉 430200）

高分辨率卫星遥感，是构成数字地球最基本的空间数据，并作为其他非空间数据的载体和框架，从而实现数字地球的空间定位［1］。迄今为止，在众多商业遥感卫星中，空间分辨率最高的是由美国数字全球公司于2001年10月18日发射的QuickBird卫星，其空间分辨率高达0.61m。QuickBird遥感技术的应用已经相当广泛，应用深度也不断加强。

遥感影像的几何纠正，是实现影像应用的前提，目的就是对遥感影像上目标的空间分布进行地图实况纠正，其实质就是采用某种数学模型，选择一定数量已知理论坐标值的特征点，获得其在底图上的坐标值，利用待定系数法求出从底图坐标向理论坐标转换的参数，进而把各要素的坐标值转换为所要求坐标系的坐标值［2］。

遥感影像几何纠正的模型很多，对于Quick－Bird这类新型高分辨率影像，不同纠正模型和纠正精度成了研究热点之一，并且针对地形图更新或者遥感图像矢量化，一般多采用多项式变换［3－6］，文献［2］也给出了不同次数多项式变换的精度分析［2］。

各种地理信息系统软件，如ERDAS、CASS、MAPINFO等，都提供了纠正模型。选择几何纠正模型时，应该从遥感影像的产品类别、工程的规模和应用范围、现有的条件和精度等方面综合考虑。

本文以合肥工业大学建筑设计院承担的中国援助非洲利比亚国家城市规划项目为背景，以QuickBird正射影像产品为基础，利用南方CASS软件，选择4种几何纠正模型进行精度的评定。

1 几何纠正模型

1.1 赫尔墨特变换

赫尔墨特变换又被称为七参数转换，分别为3个平移参数TX、TY、TZ，3个旋转参数ωX、ωY、ωZ和1个尺度参数m。

假设有2个分别基于不同基准的空间直角坐标系统OA－XAYAZA和OB－XBYBZB，则赫尔墨特变换的函数模型为：

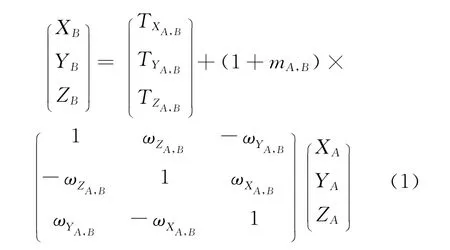
该模型在进行全球或较大范围的基准转换时较为常用，但由于旋转中心位于原始坐标参照系的原点，因而旋转参数与平移参数具有较高的相关性。

1.2 仿射变换

仿射变换也是空间直角坐标变换的一种，它是一种二维坐标到二维坐标之间的线性变换，在高等几何中，把平面到自身的保持同素性、结合性和共线性的单比不变的点变换称为仿射变换。仿射变换就是一种最常用的低阶几何变换，属于刚性变换，具有良好的数学特性。仿射变换是一种比较简单的一次变换，也是使用最多的一种几何校正的方式，其表达式为：

仿射变换的特点是：直线变换后仍是直线；平行线变换后仍是平行线；长度比随方向不同而不同，其理论基础是在视场角相对较小的情况下，摄影光束可以看作是等效的平行投影［7］，因此比较适合中小比例尺地形图成图。

1.3 线性变换

在摄影测量作业时，必须要知道相片的内外方位元素才能够求出像点的物方坐标。直接线性变换不需内方位元素值和外方位元素的初始值，而是直接建立像点坐标仪坐标和相应物点物方空间坐标之间直接的线性关系的算法。该变换是假定在小区域内遥感图像几何失真是线性变换的，当像点坐标为（x，y），地面点坐标为（X，Y）时，其数学表达式为：

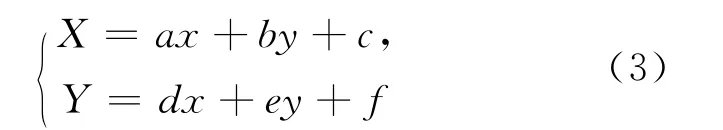
其中，a、b、c、d、e、f为模型参数。

1.4 二次变换及高次变换

二次变换或高次变换通常称为多项式变换，经常被用于图像纠正，并且不需要传感器参数方面的信息。该模型原理比较直观，计算比较简单，特别是对地面相对平坦的情况，具有足够好的纠正精度。

该算法的基本思想是回避成像的空间几何过程，而直接对影像变形的本身进行数学模拟。它认为遥感影像的总体变形可以看作平移、缩放、旋转、仿射、偏扭、弯曲以及更高次的基本变形的综合作用结果，因而纠正前后影像相应点之间的坐标关系可以用一个适当的多项式来表达，其数学模型为：

其中，P、Q代表2次以上高次项之和。（4）式是高次变换方程，符合（4）式的变换称为高次变换。如果不考虑高次变换方程中的P和Q时，则变成二次变换。

二次变换适用于原图有非线性变换的情况，至少需要6对控制点坐标及其理论值才能求出待定系数。

2 精度评定

2.1 内符合精度

根据不同数学模型的误差方程，可计算出公共点观测量拟合残差Δi，将已知点的坐标看做真值，得到未知参数单位权总误差的估值σ0，即

其中，n为公共点个数。

未知参数单位权中误差是反映未知参数解算的内符合精度，评定数学模型的稳定性和收敛性。

2.2 外符合精度

利用各数学模型将检查点进行转换后的坐标（xt，yt）与检查点的坐标（xL，yL）按照（6）式、（7）式求二维坐标残差vi和外符合精度mi0，即

其中，n为检查点的个数；mi0为外符合精度，反映数学模型的准确性和一致性。

3 实验对比

3.1 工程简介

本次实验采用某市QuickBird高分辨率商业遥感卫星正射影像数据，如图1所示。

图1 某市QuickBird遥感影像图

投影转换采用Mercator投影，基准为WGS－1984，比例尺1∶2 500，面积大约为0.4km2，地势较平坦。作业方法是采用5台Leica 1200GPS接收机布设E等GPS控制网，RTK采集像控点和检查点，如图2所示，然后进行几何纠正，利用南方CASS软件进行遥感影像的矢量化，最后进行修补测，提交某市的1∶1 000的规划用图。

图2 控制点和检查点位置示意图

3.2 实验结果及精度分析

在实验区域内采集了6个控制点作为数学模型的公共点，并评定其内符合精度，12个地物特征点作为检查点，评定各数学模型的外符合精度。4种数学模型均使用相同的公共点和检查点，结果见表1所列。

内符合精度和外符合精度的柱状图，如图3所示，其中横轴1～4表示赫尔墨特变换、仿射变换、线性变换和二次变换。

表1和图3的实验结果表明：

（1）根据文献［8］的规定，当测图单纯为城市规划用途时，对于1∶1 000比例尺的地形图，点位中误差应不大于±0.50m［8］，则赫尔墨特变换和二次变换均满足规范要求，其中二次变换的精度最高。

（2）根据仿射变换的特点，其长度比随方向的不同而不同，从而造成了某个方向的变形较大，比如Y方向最大差值达－1.494m，但仿射变换的同素性和共线性保证了外符合精度的一致性和准确性。

（3）关于二次变换和高次变换，比如三次变换等，文献［2］指出三次与二次多项式的精度相对差别不大，而在用时方面，三次多项式纠正所需时间远大于二次多项式纠正所需的时间［2］，故本实验未对高次变换进行分析。

（4）从参数的个数上分析，仿射变换和线性变换的参数要比赫尔墨特以及二次变换的少，几何纠正模型所需要的控制点的数目相对较少，但从表1中的数据看，其精度要略低于后两者。

（5）从几何纠正的时间上看，这4种变换过程所花费的时间没有明显的区别。

表1不同几何纠正变换精度比较m

图3 内外符合精度柱状图

当然，还有很多工作有待于继续深入研究，比如控制点的分布和数量对几何纠正模型精度的影响；对于地势起伏较大的区域，几何纠正模型的选择以及几何纠正过程中，外业和内业数据处理的误差源情况等等。

4 结束语

本文以具体工程案例为背景，基于南方CASS软件，对比了赫尔墨特变换、仿射变换、线性变换和二次变换4种几何纠正方法。研究表明，在小区域内，地势起伏较平坦的地区，二次变换的数学模型精度要优于其他3种，并且根据实践经验，选择的控制点要均衡分布、点位清晰，几何纠正中，遥感影像的控制点不要漏选和错选，并查看一下误差的大小是否满足精度要求，从而提高成图的质量和可信度。因此，对于1∶1 000的城市规划用图，利用QuickBird正射影像进行矢量化是一种经济、有效、实用的方法。

［1］李德仁，李清泉.地球空间信息学与数字地球［J］.地球科学进展，1999（12）：535－540.

［2］陈于林，秦 军.LANDSAT－7卫星图像预处理的几何纠正［J］.铁道勘察，2005（4）：16－18.

［3］鲍建宽，陈文慧.基于QuickBird影像和GPS RTK的土地利用现状图测绘［J］.测绘与空间地理信息，2009（2）：25－28.

［4］柴红梅，李津岭，张 健.利用QuickBird影像快速更新1∶2 000地形图技术方法探讨［J］.城市勘测，2010（3）：85－87.

［5］赵秀英.利用QuickBird卫星数据制作大庆油田1∶5 000地形图［D］.长春：吉林大学，2005.

［6］李 爽，李小娟，孙英君，等.遥感制图中几何纠正精度评价［J］.首都师范大学学报：自然科学版，2008，29（6）：89－92.

［7］王利英.基于RFM的IKONOS遥感影像几何纠正方法研究［D］.阜新：辽宁工程技术大学，2007.

［8］GB／T 14912－2005，1∶500 1∶1 000 1∶2 000外业数字测图技术规程［S］.