多核系统上任意2序列公共元素的并行查找
2012-06-05蔡德霞韦兴柳林孔升
蔡德霞, 钟 诚, 韦兴柳, 林孔升
(广西大学 计算机与电子信息学院,广西 南宁 530004)
任意2序列公共元素的查找问题可应用于数据库、统计、运筹学和组合学等领域。文献[1]研究了由有序序列x和y组成的排序矩阵上的并行查找问题,并指出可使用排序矩阵上的并行查找思想来实现任意2序列公共元素的查找问题。文献[2]设计了PRAM模型上任意2序列公共元素的并行查找算法。近年来,多核结构发展成为微处理器的主流,它支持缓存高效和线程级并行[3],具有高度的并行处理能力[4]。文献[5]采取将线性方程组的增广矩阵按行划分并合理分布到各级缓存,各个处理核以多线程方式并行计算矩阵行的方法,设计了多核系统上线程级并行求解n阶线性方程组的算法。文献[6]利用软件多线程技术和多核结构中的多级Cache机制,基于可分负载理论的最优原则,针对Multisets数据序列的特点,提出一种多轮非周期性的数据序列最优分配模型,进而设计实现进程级与线程级并行的Multisets排序算法。文献[7]从综合提高多核计算机共享二级缓存的利用率、矩阵存储的数据结构优化、计算与访存重叠操作、缓存无关等角度出发,提出适合矩阵乘积问题并行计算的数据分布和调度策略,设计实现非递归、高效和可扩展的矩阵乘积并行算法。
本文采用数据多级分块技术、数据局部性原理和循环并行优化方法,充分利用多核处理器的多级存储和多线程技术,设计实现多核系统上存储高效、线程级并行、扩展性好的任意2序列公共元素的并行查找算法。
1 算法的设计与分析
1.1 算法的设计
多核系统上任意2序列公共元素并行查找算法描述为:
(1)p个处理核心应用并行快速排序算法[8]分别对数据序列a、b进行排序。
(2)如果排序后的数据序列a的最小值大于排序后的数据序列b的最大值,或者数据序列a的最大值小于排序后的数据序列b的最小值,则数据序列a和数据序列b无公共元素。
(3)将主存中的数据序列b根据二级缓存大小的利用率来进行分块,每组数据块的大小为θC2,数据序列b分为m/(θC2)组,依次从主存调入二级缓存。接着对分配到二级缓存的数据再进行分块,划分的依据是一级缓存大小的利用率,每块数据块的大小为βC1,共θC2/(pβC1)块,各个数据块分别映射到各个处理器核心。因为进行数据划分后映射到各个处理器核心的数据在处理过程中不需要进行交换,因此各个处理器核心之间不存在数据的移动问题。
(4)求出序列b划分后存到各处理器核心一级缓存中的数据块bi的最小值min和最大值max,min=b[(i-1)βC1],max=b[iβC1-1]。为减少序列b中元素的移动,应将序列a进行分块,将序列a中符合区间(b(i-1)βC1,b(iβC1-1)]的数据映射到数据块bi所在的处理器核心。
(5)各个处理器核心并行调用串行的二分查找方法,查找数据块ai和bi是否具有公共元素,如果存在,将公共元素保存并统计公共元素个数k。因为并行调用串行的二分查找方法,在各个处理器核心查找数据块ai和bi的公共元素操作结束时不能立即确定出公共元素的数目,所以需要设定一个共享数组c[i](i的取值为数据序列b划分到一级缓存的总块数)来保存数据块ai和bi的公共元素的个数,在查找操作前需给数组c中各元素赋以初值零。在数据序列a和数据b的所有数据块都完成查找操作后,c[i]保存各个数据块的查找结果,根据c数组可以统计出数据序列a和数据序列b的公共元素的总数k。
1.2 算法的正确性
本算法的关键点是要保证公共元素个数k≠0或者k≠n时k值的正确性,而保证k≠0或者k≠n的正确性的关键操作是要保证划分到一级缓存中的数据块ai的元素的取值范围为(b(i-1)βC1,b(iβC1-1)],查找成功后元素保存到数组c[i]中。
中国在棉纺织业的发展战略上指出要充分利用“一带一路”的战略机遇,与棉纺织业成长迅速的发展中国家进行合作,实现资源优化配置;发展新疆及西部纺织行业。新疆自治区在2016年发布了关于纺织服装产业补贴管理办法。其中提到在原有的相关优惠政策不变的前提下。同时新增了预拨补贴资金、加快兑付进度、对运费补贴实行动态管理以及简化资金拨付程序等方面的内容。
因为数据序列a元素分块时的划分是依据当前存储在一级缓存中的数据块bi的最小值min和最大值max,所以在进行查找公共元素操作时,能保证数据块ai和bi的元素处于相同的取值区间,这样就能保证查找的正确性。因为算法执行过程中各个处理器核心是并行进行二分查找操作,查找成功后,为了防止并行写冲突,采用中间数组c来保存查找结果可解决并行写冲突问题。数组c的下标取值范围为[0,m/(pβC1)],每一组数据块ai和bi成功查找后的结果保存于c[i](i为数据序列b划分后的第i个数据块),这样可以保证各个处理器核心查找成功后的结果能并行地写入数组c。
1.3 算法复杂度分析
算法步骤(1)中p个处理核心对整数序列a和b排序的时间为O(n+nlb(n/p));步骤(2)可在O(1)时间内完成;步骤(3)对整数序列a和整数序列b进行数据划分后映射到各3个处理器核心,使得整数序列a和整数序列b中的数据在处理过程中不需要进行交换,该步骤可在减少主存和L2Cache、L2Cache和L1Cache之间数据交换的同时也使得各个处理器核心之间不存在数据的移动问题。因此,对于支持的多核系统,算法(3)~(4)步的完成时间为O(m/(θC2))×O(θC2/(p2βC1))=O(m/(p2βC1))。步骤(5)每个处理核心调用二分查找算法查找数据块ai和bi的公共元素,假设数据块ai的规模为si,数据块bi的规模为sj=βC1,于是该步骤可在O(silb(βC1))时间内完成。
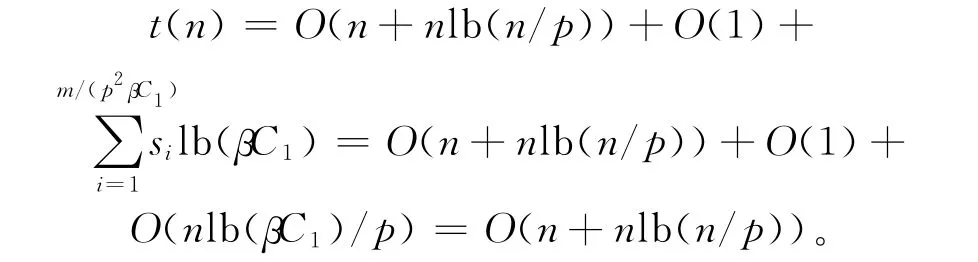
本文给出的并行算法的加速度为:
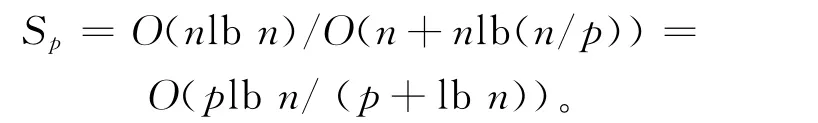

本文给出的并行算法的执行代价为:当处理核心数目p<lbn时,本文给出的并行算法获得了线性加速并且执行代价是最优的。
2 实验
2.1 实验环境
实验的硬件平台为Intel(R)Xeron(R)E5405 2.0GHz四核计算机,二级缓存容量为12Mb,一级缓存容量为128kb,操作系统为Red Hat Enterprise Linux 5,采用OpenMP和C语言编程实现本文的多核系统上任意2序列公共元素并行查找算法。
2.2 实验结果与分析
实验假设数据序列a和b的数据规模相等,在四核计算机上,通过采用动态关闭处理核的方法,考虑了处理器核数、数据序列的规模及线程数等因素,测试了多核系统上任意2序列公共元素的并行查找算法的运行时间和加速比,并与非分块的任意2序列公共元素的并行查找算法(简称非分块算法)[2]的运行时间进行了对比。
不同数据规模,线程数增加,运行不同的处理器核数时,多核系统上任意2序列公共元素的并行查找算法的运行时间如图1所示。
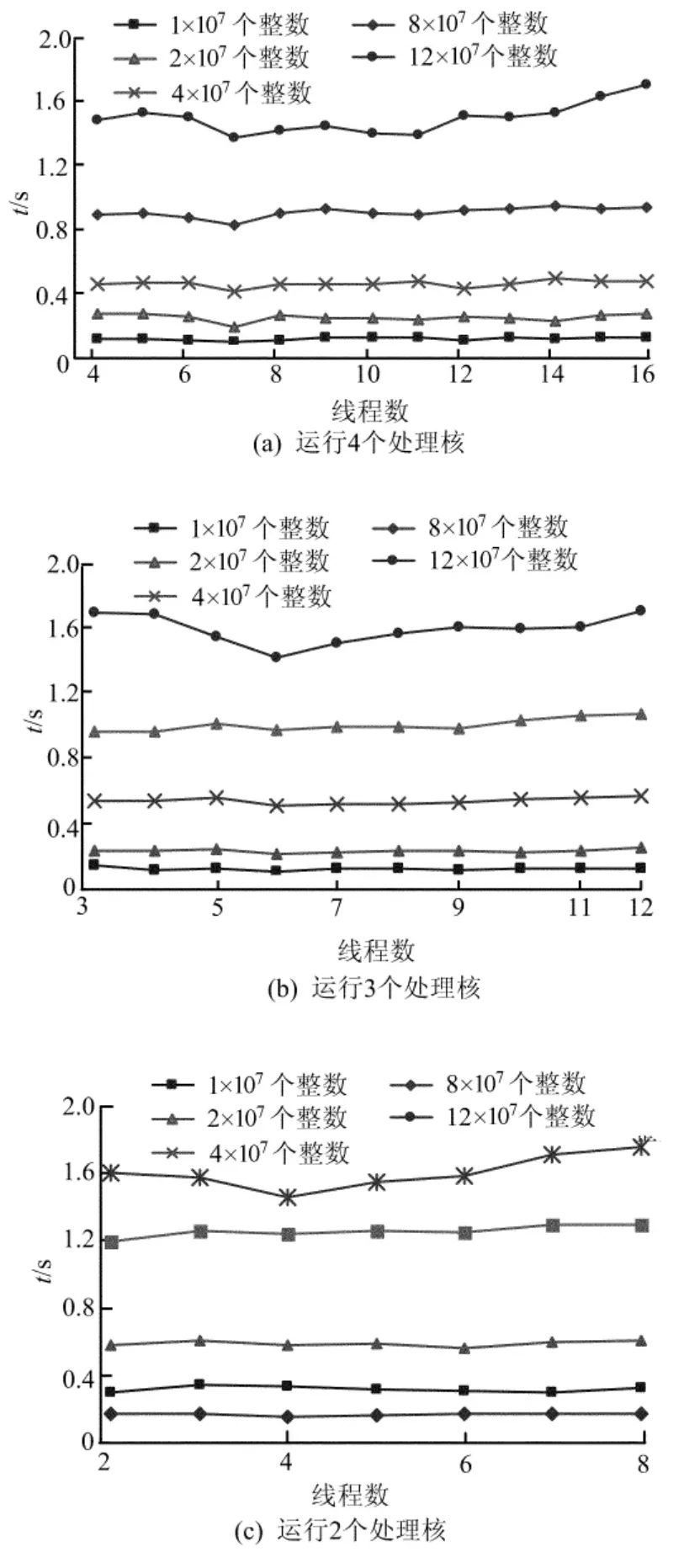
图1 运行不同数量处理核本文算法所需的时间
从图1a可看出,对不同数据规模,运行4个处理核时,线程数为7~12时算法的运行时间较好,其中线程数为7时最佳。从图1b可看出,对不同数据规模,运行3个处理核时,线程数为6~10时算法的运行时间较好,其中线程数为6时最佳。从图1c可看出,对不同数据规模,运行2个处理核时,线程数为4~7时算法的运行时间较好,其中线程数为4时最佳。由图1可看出,对于不同处理核数目,其最佳线程数也不同,线程数约为2倍处理核数目时,算法的运行时间最少。此外,当线程数大于3倍处理核数目时,随着线程数目的增加,线程对处理器的竞争会随之增大,线程的启动/停止、上下文切换会产生更大的额外开销,因此,算法的运行时间会逐渐上升。
输入数据规模分别为 1×107、2×107、4×107、8×107、12×107个整数时,随着处理核数目的增加,采用最佳线程数执行多核系统上任意2序列公共元素的并行查找算法所消耗的执行时间如图2所示。
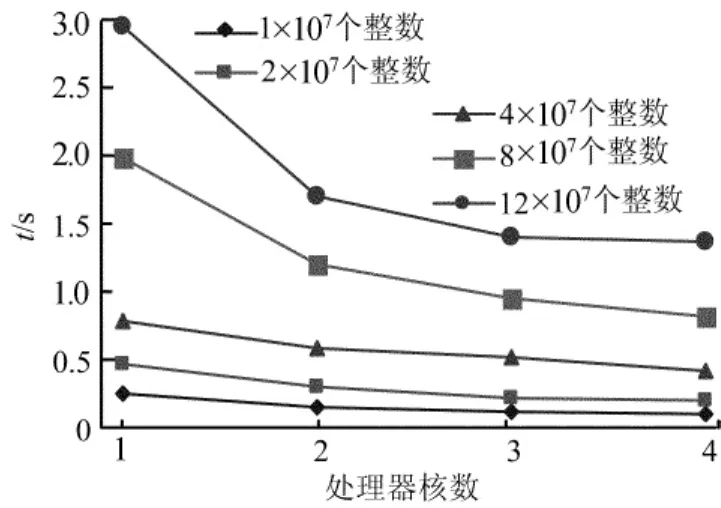
图2 采用最佳线程数执行本文查找算法的运行时间
从图2可看出,随着处理核数目的增加,多核系统上任意2序列公共元素的并行查找算法显著下降,运行时间下降趋势变得缓慢。这是因为多核系统的通信开销会随着处理核心数目的增加而变得越来越大,并且多个处理核心访问共享资源也会逐渐增大时间开销。
不同数据规模,随着处理核数目的增加,采用最佳线程数运行多核系统上任意2序列公共元素的并行查找算法的加速比如图3所示。
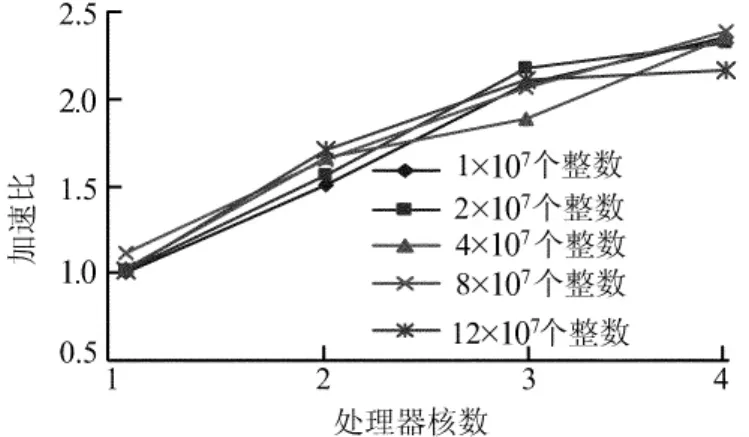
图3 采用最佳线程数执行本文算法的加速比
图3的实验结果表明,随着处理核数目的增加,多核系统上任意2序列公共元素的并行查找算法的加速比逐渐增大,接近于对数加速。
多核系统上任意2序列公共元素的并行查找算法的等效率函数曲线如图4所示。从图4可以看出,对于2个任意规模的输入数据序列,为了维持等效率,本文提出算法的工作量随着处理核数目呈现近似亚线性的增长。这表明本文所提出的算法具有较好的可扩展性。

图4 采用最佳线程数执行本文算法的等效率曲线
对于相同数据序列,在四核计算机上,采用最佳线程数执行本文提出的多核系统上任意2序列公共元素的并行查找算法与非分块算法在运行时间上的对比如图5所示。
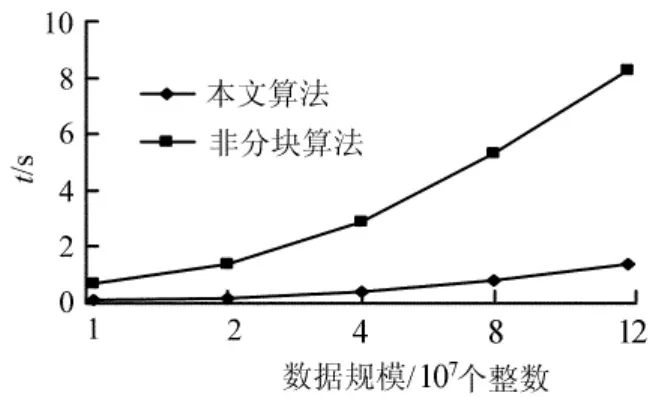
图5 采用最佳线程数执行本文算法和非分块算法的运行时间
从图5可知,本文算法明显优于非分块算法,这是因为本文算法充分利用二级缓存和一级缓存来提高数据的局部性,避免缓存缺失性,能减少非分块算法中出现的数据频繁交换操作。此外,随着数据规模的增加,本文算法的优异性更加明显,这说明当数据规模很大时,在多核系统上有效利用二级缓存,采用数据多级分块技术可以更有效地求解任意2序列公共元素的并行查找问题。
运行4个处理核时,对不同的数据规模,采用最佳线程数,二级缓存利用率θ增加时运行本文算法所需要的时间如图6所示。从图6可看出,二级缓存的利用率对本文算法的性能是一个很重要的影响因素。当θ=0.6时,本文算法的运行时间效果较好,当θ>0.6,随着θ的增大,本文算法的时间性能下降。由此可知,在算法运行过程中,对于数据划分,应分配合适的数据存储到二级缓存,划分时要预留一定的空间来存放中间结果、指令代码以及算法运行过程中所产生的一些额外开销。
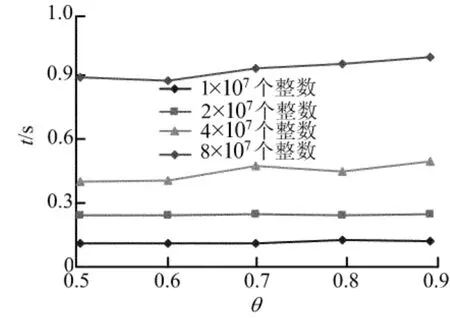
图6 二级缓存利用率增加时本文算法的运行时间
3 结束语
本文充分利用多核计算机的多级存储和数据多级分块技术以及数据局部性方法,将给定的2序列划分适合于二级缓存大小的数据块以减少主存和二级缓存之间数据的交换;通过将存储在二级缓存中的数据平均分配给一级缓存,减少了二级缓存和一级缓存数据交换,使得大大减少处理核之间通信时间的同时,能确保处理核之间的数据负载均衡。并行多线程技术和循环并行优化方法设计的多核系统上任意2序列公共元素并行查找算法高效、可扩展。进一步的工作是基于多核机群系统,研究设计存储和通信高效、加速比和可扩展性好的任意2序列公共元素的并行查找算法。
[1]Cosnard M,Ferreira A.Parallel algorithms for searching inx+y[C]//Proc of the 1989International Conference on Parallel Processing,1989:16-19.
[2]钟 诚.任意两序列公共元素的并行查找[J].微电子学与计算机,1993(9):18-20.
[3]Akhter S,Robert J.Multi-core programming:increasing performance through software multi-threading[M].北京:电子工业出版社,2007:45-70.
[4]李晓明,王 韬,刘 东,等.走进多核时代[J].计算机科学与探索,2008,2(6):562-570.
[5]冯 佩,钟 诚,韦 伟.多核多线程并行求解线性方程组[J].合肥工业大学学报:自然科学版,2011,34(2):237-240,250.
[6]Zhong Cheng,Qu Zengyan,Yang Feng,et al.Parallel multisets sorting using aperiodic multi-round distribution strategy on heterogeneous multi-core clusters[C]//Proc of 3rd International Symposium on Parallel Architectures,Algorithms and Programming.IEEE Computer Society Press,2010:247-254.
[7]鹿中龙,钟 诚,黄华林.多核计算机上非递归并行计算矩阵乘积[J].小型微型计算机系统,2011,32(5):860-866.
[8]陈国良,安 虹,陈 崚,等.并行算法实践[M].北京:高等教育出版社,2004:185-187.
