大齿轮齿形测量中补偿安装偏心的理论分析

郭敬滨，张大厦，张继承

大齿轮齿形测量中补偿安装偏心的理论分析

郭敬滨，张大厦，张继承

(天津大学精密测试技术及仪器国家重点实验室，天津 300072)

针对大齿轮齿形测量时安装偏心不易消除的特点，采用误差补偿的原理消除安装偏心产生的测量误差．分析了安装偏心与齿轮传动时啮合线增量的关系，提出了实时和非实时的误差补偿方法．实时误差补偿的核心思想是坐标变换，结合齿形的各种测量方法，给出补偿安装偏心产生的测量误差的数学模型；非实时误差补偿是在测量结束后利用计算机辅助计算补偿安装偏心产生的测量误差，推导了啮合线增量法和微分法的数学模型．实际测量时，可根据实际情况选择合适的补偿方法．

大齿轮；安装偏心；误差补偿；齿形偏差

大齿轮通常指大直径、大模数的齿轮，广泛应用于船舶、冶金、采矿、发电等设备中．随着现代工业和科学技术的发展，对大齿轮的精度要求越来越高．在国家大力发展的低碳能源-风力发电中，风电增速齿轮箱是风力发电机组的关键部件，它采用的大齿轮精度非常高，所以测量精度要求也很高．大齿轮测量过程中，测量仪器回转工作台的回转轴线与大齿轮的几何中心很难重合，这样就产生了安装偏心[1-2]．由于大齿轮具有尺寸大、质量大等特点，采用调整的方式消除安装偏心既费时费力又不经济，所以采用误差补偿的方法消除安装偏心产生的齿形偏差[3-4]．

误差补偿根据时效性可以分为实时误差补偿和非实时误差补偿 2种．笔者根据补偿安装偏心的基本原理，结合不同的测量方法，论述 2种误差补偿策略的应用．

1 补偿安装偏心的基本原理

根据齿轮运动学的误差理论，齿轮误差是通过啮合线(齿形的法线)影响齿轮传动性能的，因此在啮合线上分析啮合线增量就能建立安装偏心产生齿形偏差的数学模型．

在测量过程中，齿轮绕回转中心O′旋转，从回转中心O′指向几何中心O的向量 O′ O为旋转矢量，即安装偏心向量．安装偏心向量 O′ O在啮合线方向上的投影即为安装偏心产生的啮合线增量[5]．为分析方便，以左右啮合线正方向对称位置作为y′轴，不失一般性．设安装偏心向量 O′ O与O′ y′的夹角为安装偏心的相位角ψ，当 0ψ= 时，安装偏心与啮合线增量的关系如图1所示．

图1 安装偏心产生啮合线增量的示意Fig.1 Schematic diagram of meshing line increment generated by installation eccentricity

当安装偏心向量 O ′O从零位起逆时针转动φ时，安装偏心在左、右啮合线上产生的增量为

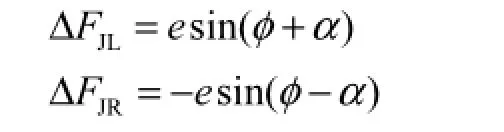
式中：e为安装偏心向量的幅值；φ为仪器坐标系下的齿轮转角；α为分度圆压力角．

在齿形有效工作部分中，安装偏心产生的啮合线增量的变化量为安装偏心产生的齿形偏差．将测量得到的总的齿形偏差减去安装偏心产生的齿形偏差，就消除了安装偏心的影响．

2 实时误差补偿的研究和应用

实时误差补偿采用坐标变换的思想，将仪器坐标系下采集到的数据变换到工件坐标下，然后进行齿形偏差的评定．应用坐标变换补偿安装偏心产生的齿形偏差，应根据齿形的测量方法，选择相应的测量仪器和控制策略．

2.1 基于法线极坐标法的安装偏心补偿

将被测齿轮安装在齿轮测量中心的回转工作台上，被测齿轮随回转轴φ做旋转运动．在以几何中心O为中心建立的工件坐标系Oxy下，测微装置的运动方向和测量方向始终与齿形的法线方向保持一致，x轴和φ轴联动即可实现；在以测量回转中心O′为中心建立的仪器坐标系O x y′′′下，测量回转中心O′到测微装置运动方向的距离O K′是不断变化的，测量时为保证测微装置的运动方向和测量方向始终与齿形的法线方向保持一致，测微装置应能沿x′轴和y′轴运动，因此要求x′轴、y′轴和φ轴联动，如图2所示．

图2 基于法线极坐标法的安装偏心补偿模型Fig.2 Compensation model of installation eccentricity based on normal polar coordinate method

当回转工作台转过角度iφ时，被测齿面上第i点的法线与x轴平行，工件坐标系下测球中心1O的坐标值为

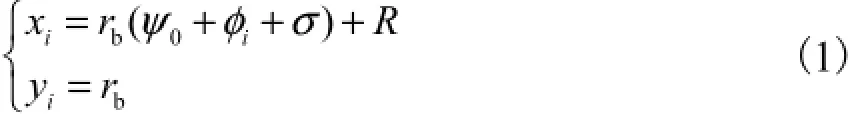
仪器坐标系与工件坐标系的关系式为

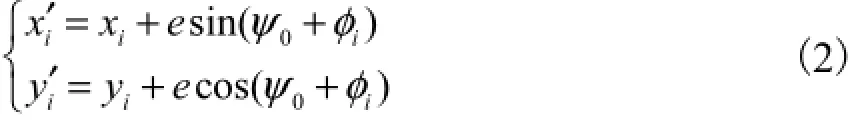
式中：0ψ为起测点处安装偏心向量的相位角；σ为起始偏角(渐开线起始点的向径与安装偏心向量的夹角)．

测球中心1O的坐标值可用各坐标轴的示值和测微装置的示值表示为测微装置的示值．第i点的展开长度为，通过坐标变换移动到仪器坐标系下，，展开角．将起测点作为测量基准点，根据渐开线齿形偏差的计算公式可得齿轮本身的齿形误差[6]为

该齿面的齿形偏差为

2.2 基于直角坐标法的安装偏心补偿

将被测齿轮安装在齿轮测量中心的回转工作台上，被测齿轮可绕回转轴φ旋转，以测量回转中心O′为中心建立仪器坐标系O x y′′′，以几何中心O为中心建立工件坐标系Oxy，如图 3所示．没有安装偏心的情况下(即工件坐标系下)，通常以齿槽中心线为y轴，被测齿轮固定不动，在垂直轴线的平面内对渐开线齿形作 -x y直角坐标测量，测微装置的测量方向与x轴平行．存在安装偏心时(即仪器坐标系下)，应使齿槽中心线与y′轴平行．

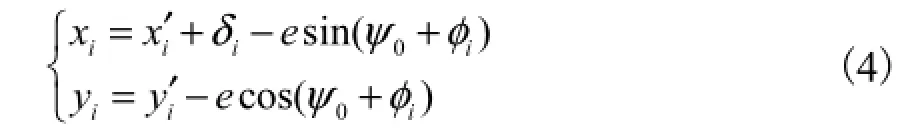
仪器坐标系与工件坐标系的关系式为式中：iφ为仪器坐标系下的齿轮转角；iδ为测微装置的示值．

上述被测点坐标已经消除了安装偏心的影响，按照齿形偏差的评定方法处理就可以得到该齿面的齿形偏差．

如图 3所示，A为理论被测点，实际被测点P位于渐开线的法线GA上，工件坐标系Oxy下P点的坐标满足方程式，由此可得

图3 基于直角坐标法的安装偏心补偿模型Fig.3 Compensation model of installation eccentricity based on cartesian coordinate method

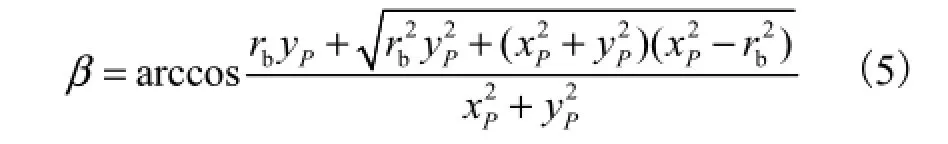
理论被测点A对应的展开角为

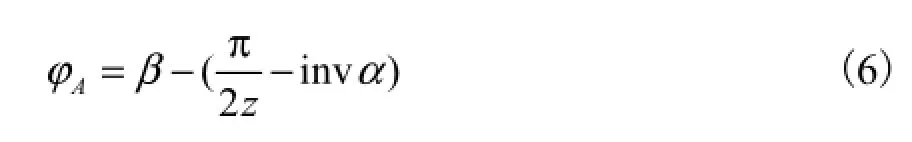
式中：α为分度圆压力角；z为齿数．

实际被测点P的齿形偏差[7]为

整理式(4)、式(6)、式(7)得被测齿面上任意点的实际齿形偏差为

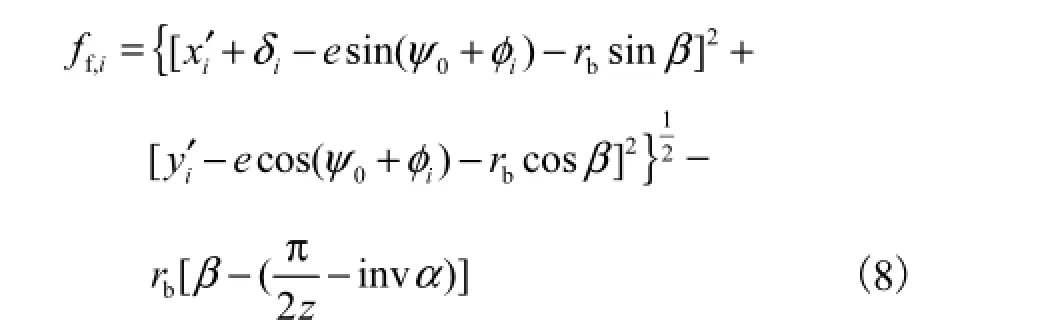
该齿面的齿形偏差为

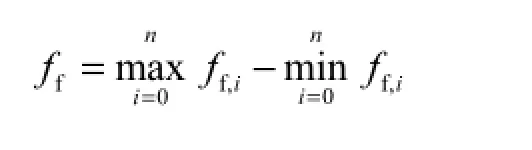
3 非实时误差补偿的研究和应用

非实时误差补偿，即在测量过程结束后，通过计算机辅助计算补偿安装偏心产生的测量误差．这种方法主要用于法线极坐标测量法，它不改变原仪器的测量方法，比较适用．

3.1 啮合线增量法

测量时，将被测齿轮安装在齿轮测量中心的回转工作台上，被测齿轮随回转轴φ做旋转运动，以齿轮的基圆半径br为半径的圆作测量基准圆，测微装置的测量方向是测量基准圆的切线方向．根据齿轮参数，通过y′轴确定测微装置的运动方向HA后，y′轴固定不动，测微装置的测量方向与运动方向一致，实际上这种测量方法在测量过程中仅需要x′轴和φ轴联动，如图 4所示．由于安装偏心的存在，测微装置的测量方向HA与齿形的法线方向NA不一致，经理论分析得知由此引入的非线性误差对测量结果影响非常小，故可以忽略．

根据补偿安装偏心的基本原理可知，安装偏心在起测点对应的啮合线增量为

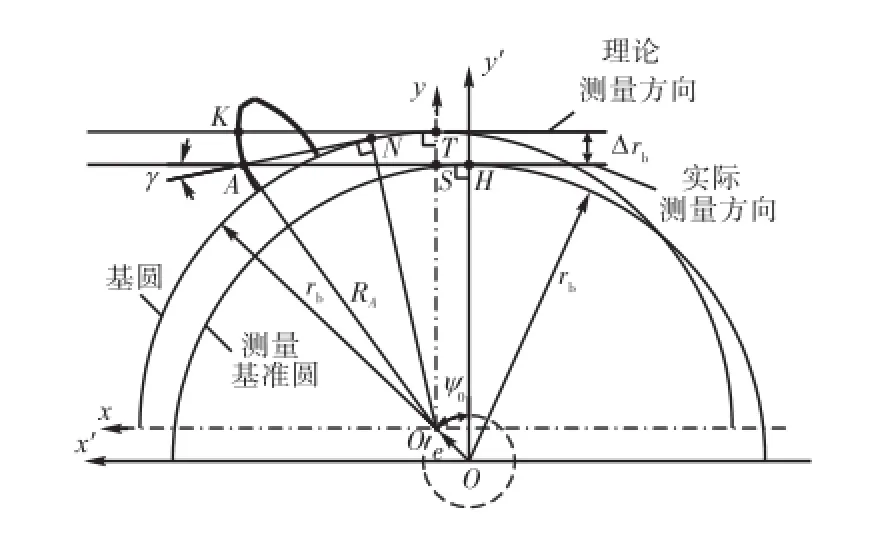
图4 啮合线增量法的安装偏心补偿模型Fig.4 Compensation model of installation eccentricity based on meshing line increment

安装偏心在齿面上任意点对应的啮合线增量为

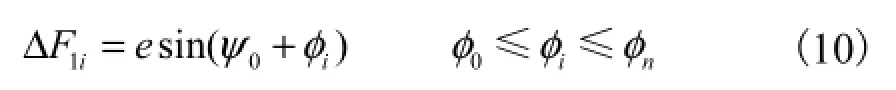
设各采样点总的齿形偏差(包括安装偏心引起的各采样点的啮合线增量)为为每个齿面上的采样点数．

补偿安装偏心后，各采样点处的实际齿形偏差ff,i为

该齿的实际齿形偏差[8-9]为

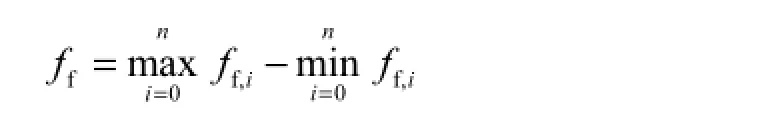
式中：ix为测微装置沿x轴移动的位移量；iδ为测微装置的读数值．

3.2 微分法

这种误差补偿方法的测量方式与基于2轴联动的啮合线增量法相同，这里不再详述．微分法与啮合线增量法的区别在于数据处理的方式不同．

根据渐开线的法线极坐标方程式可知

式中：L为被测点的展开长度；br为基圆半径；φ为被测点对应的展开角．

对法线极坐标方程式两边微分得

式中：LΔ 为安装偏心产生的啮合线增量；brΔ 为存在安装偏心时基圆半径变化量；φΔ 为存在安装偏心时齿轮转角的变化量．

根据式(13)，只需要求得brΔ 和 φΔ 就能得到安装偏心产生的齿形偏差．

如图 4所示，K相对于齿轮几何中心O的展开角与A相对于齿轮测量回转中心O′的展开角之差为Δφ，且有

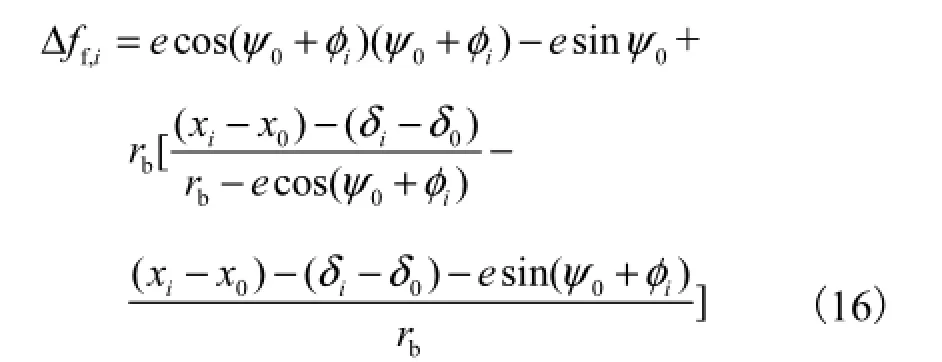
设各采样点总的齿形偏差(包括安装偏心引起的各采样点的啮合线增量)为为每个齿面上的采样点数．

补偿安装偏心后，各采样点处的实际齿形偏差为

该齿的实际齿形偏差为

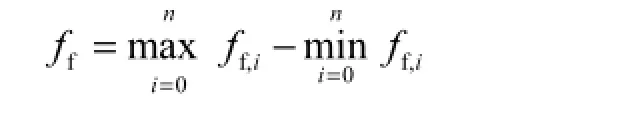
4 结 语

通过理论分析和测量实践可知，补偿大齿轮安装偏心的方法因齿形测量方法不同而有所差异．另外，不同测量仪器对控制策略的要求也不同，采用实时误差补偿时，法线极坐标法要求 3轴联动；而直角坐标法要求 2轴联动．非实时误差补偿不改变原仪器的测量方法和控制策略，比较适用．实际测量中，可根据实际情况选择合适的补偿方法．

［1］ 单光坤，李文龙，郑 鹏，等. 大型齿轮在机测量中安装偏心的测定及补偿[J]. 机械传动，2003，27 (2)：48-50.

Shan Guangkun，Li Wenlong，Zheng Peng，et al. Measurement and compensation of eccentricity in the on-machine inspection of large gears[J]. Journal of Mechanical Transmission，2003，27(2)：48-50(in Chinese)．

［2］ Oiwa Takaaki，Yoshida Osamu. In-process measurement for gear eccentricity[J]. Journal of the Japan Society for Precision Engineering，2002，68(2)：244-250.

［3］ Jin Jiaqi，Dong Lei，Zhao Fenghui. Measuring principle and technology of accumulate pitch error of large gear[C]// Proceedings of SPIE：The International Society for Optical Engineering. Gwangju，Korea，2010，7500(750003).

［4］ Jin J Q，Duan Z Y，Wang Q，et al. In-suit integrated measurement of profile precision of large gears based on rack-shaped-edge probe[J]. International Journal of Materials and Product Technology，2008，31(1)：97-105.

［5］ 庄葆华，李 真. 近代齿轮测量技术与仪器[M]. 北京：机械工业出版社，1986.

Zhuang Baohua，Li Zhen. Modern Measurement Technology and Instrument of Gears[M]. Beijing：China Machine Press，1986(in Chinese).

［6］ 卢春霞，劳奇成，李 平，等. 偏心圆齿轮齿形误差的测量[J]. 西安工业学院学报，1999，11(1)：71-74.

Lu Chunxia，Lao Qicheng，Li Ping，et al. The tooth profile measurement of an eccentric gear[J]. Journal of Xi’an Institute of Technology，1999，11(1)：71-74(in Chinese).

［7］ 严 军，石照耀. 求解齿轮齿廓误差的新算法[J]. 工具技术，1999，33(2)：37-38.

Yan Jun，Shi Zhaoyao. New algorithm of profile deviation of gears[J]. Tool Engineering，1999，33(2)：37-38(in Chinese)．

［8］ Munro R G，Linq P H K. New method of measuring involute profile deviations of gear teeth[J]. Proceedings of the Institution of Mechanical Engineers(Part C)：Journal of Mechanical Engineering Science，1996，210(1)：63-67.

［9］ Kurokawa S，Ariura Y. Transmission error analysis of involute cylindrical gears with radial eccentricity：Measurement of eccentricity and the influence of cumulative pitch deviations[J]. VDI-Berichte，2002，1665 (2)：1003-1017.

Compensation Theory Analysis of Installation Eccentricity in Measurement of Large Gear Tooth

GUO Jing-bin，ZHANG Da-sha，ZHANG Ji-cheng
(State Key Laboratory of Precision Measuring Technology and Instruments，Tianjin University，Tianjin 300072，China)

With regard to the fact that installation eccentricity is not easily dismissed in the measurement of large gear tooth，the principle of error compensation was adopted to eliminate the measurement error generated by installation eccentricity. The relationship between installation eccentricity and meshing line increment in the gear transmission was analyzed. The real time error compensation and the non-real time error compensation are proposed. Coordinate transformation was the core idea of the real time error compensation. Combined with a variety of profile measurement methods，the compensation model of the measurement error generated by installation eccentricity was presented. In the non-real time error compensation，the measurement error generated by installation eccentricity was compensated by computer-aided calculation after the measurement. The error compensation models based on meshing line increment and differential were derived. In the actual measurement，the proper compensation method can be chosen according to actual condition.

large gear；installation eccentricity；error compensation；involute profile deviation

TB92

A

0493-2137(2012)05-0435-05

2010-10-27；

2010-12-15.

郭敬滨（1959— ），硕士，副教授．

郭敬滨，guojingbin@tju.edu.cn．