中下承式拱桥吊杆应力冲击系数不均匀性研究
2012-06-05朱劲松
朱劲松,邑 强
(1.天津大学 建筑工程学院,天津 300072;2.天津大学 滨海土木工程结构与安全教育部重点实验室,天津 300072)
拱桥吊杆是中下承式拱桥的关键受力构件。吊杆失效轻则引起吊杆静张力的重分布[1],对拱桥结构整体受力安全产生不利影响,重则引起桥面坍塌等恶性事故的发生。引起吊杆失效甚至过早失效的主要原因是吊杆在运营中受到车辆荷载作用。更重要的是,车辆过桥还会对吊杆产生冲击作用,增大其循环应力幅。对于桥梁的不同部位,车辆荷载所产生的冲击效应也不一致[2],车辆对拱桥吊杆产生的冲击作用亦是如此。因此,有必要对吊杆所受冲击效应不均匀性进行研究,研究结果对拱桥吊杆的设计以及运营期维护具有指导意义。
国内外很多学者对桥梁结构所受移动车辆荷载冲击效应进行了研究,并取得了显著的成果。Huang[3]对跨度在200 m以内的中承式钢管混凝土拱桥的动力特性和冲击系数进行了研究,提出了相关的计算公式。文献[4]对简支梁桥在移动车辆荷载作用下的动力冲击效应进行了计算分析与现场试验研究。文献[5]采用7自由度的整车模型,混凝土裂缝分为开口裂缝和呼吸裂缝两种类型,对不同裂缝类型、裂缝出现位置、裂缝参数及车辆组合等因素对桥梁冲击系数的影响进行了分析。文献[6]利用多体系统动力学软件SIMPACK建立三维空间车辆精细化模型,针对琼洲海峡跨海超大跨度斜拉桥方案,采用基于多体系统动力学与有限元结合的联合仿真技术,计算列车以不同车速单线行车和双向对开通过该大跨度斜拉桥的空间耦合振动响应。文献[7]基于ANSYS提出了简便的分离迭代解法进行车桥耦合振动分析,考虑车辆在曲线梁桥上的行驶偏心,分析了曲率半径和车速对曲线梁桥冲击效应的影响。Bruno等[8]研究了大跨度斜拉桥在移动荷载作用下的动力响应,分析了包括斜拉索在内的结构多处的动力冲击系数。Lei等[9]分析了大跨箱型梁桥在车辆荷载作用下的动力响应。Hamidi等[10]分析了车辆轴距与桥梁跨度的比值对结构动力响应的影响,并提出了简支梁桥动力冲击系数取用参考公式。Wu等[11-12]中提出了车桥耦合振动中各参数都具有不确定性,作者以能够考虑这些不确定因素的随机有限元法分析了桥梁结构在移动车辆作用下的动力响应。但大部分研究都集中在桥梁主梁在车辆荷载作用下的动力反应,主要关注跨中位移、速度、加速度响应,很少关注移动车辆荷载对拱桥吊杆的动力冲击作用。
为了分析公路车辆动力作用下的拱桥吊杆冲击系数不均匀性,本文基于D'Alembert原理,导出了两轴车辆模型的振动方程,根据车辆与桥梁接触点处位移与力的协调条件耦合二者的振动方程,并且考虑了桥上路面不平顺的影响;采用Newmark-β求解,编制了计算程序VBAP;最后以某钢管混凝土拱桥为例,利用本文方法与程序分析了结构阻尼、桥上路面粗糙度、车重及车速对吊杆应力冲击系数的影响。所得结论可为同类桥梁吊杆设计与运营期的维护提供理论指导。
1 动力响应分析
1.1 桥梁模型
为了分析拱桥在行驶车辆作用下的动力响应,本文对桥梁结构进行了有限元离散。离散后,桥梁动力方程为:
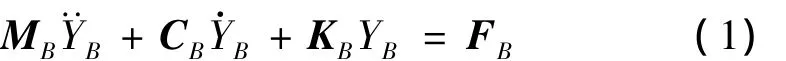
本文以瑞雷阻尼[13]的形式考虑桥梁结构阻尼:

式中,C为结构的阻尼矩阵,M,K分别为结构质量矩阵和刚度矩阵。α0,β0由式(3)、(4)求得:

式中:ω01,ω02分别为结构第一阶和第二阶自振频率。ξ1,ξ2分别为结构的第一阶和第二阶模态阻尼。
1.2 车辆模型
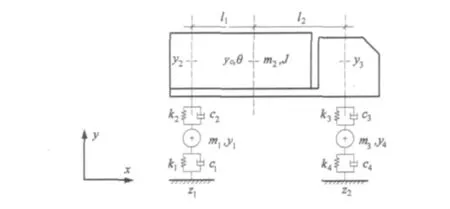
图1 车辆模型Fig.1 Model of vehicle
将车辆简化为如图1所示的两轴车力学模型。车体简化为一个具有质量m2,绕质心转动惯量为J的刚体,两轴距离为l,车轮的质量分别为m1,m3。车轮与地面的相互作用以及车体与车轮之间的连接均用弹簧阻尼系统模拟。车轮与桥面相互作用的刚度系数与阻尼系数分别为k1,c1以及k4,c4,车体与车轮间连接的刚度与阻尼系数分别为k2,c2和k3,c3。该模型具有8个自由度,即车轮的竖向位移y1,y4,车轮与桥面接触处的位移z1,z2,车体两端的竖向位移 y2,y3,车体质心处的位移和转角yc,θ。其中z1,z2与桥面位移耦合,yc,θ 可用 y2,y3表示,即:

因此该模型独立自由度共四个,其位移向量可写成:
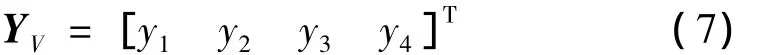
对车辆各刚体进行受力分析,根据达朗贝尔原理可列出车辆的振动方程:
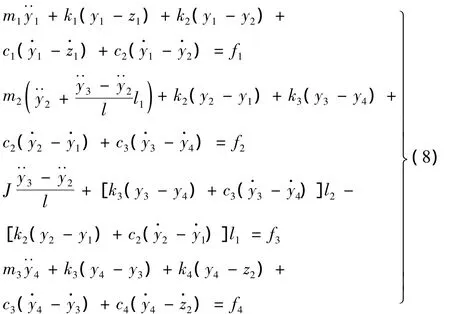
为便于编程,将方程整理成矩阵形式:
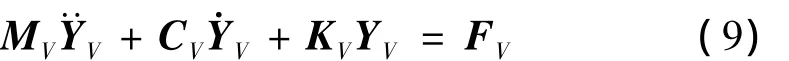
其中:
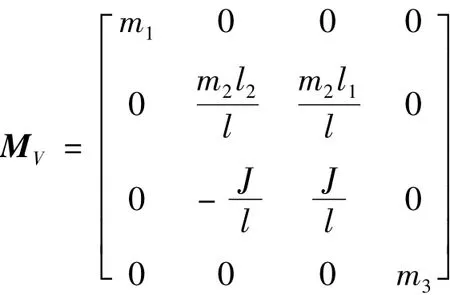


表1 车辆模型参数Tab.1 Parameters of vehicle model
本文所用20 t车辆模型参数如表1所示[9],在此基础上通过修改车体质量m2得到15 t,30 t车辆参数。
1.3 桥面粗糙度模型

表2 路面分级情况Tab.2 Road surface classification
桥上路面不平顺在车桥耦合振动中不容忽视。由文献[14]可知,桥面不平顺可描述为一个零均值服从稳态Gauss分布的随机过程,给定路面不平顺功率谱后,可通过多种方法模拟得到路面不平顺样本。本文采用三角级数叠加法[15]模拟路面不平顺:


其中,r(x)为路面不平顺样本函数,αk为余弦函数的幅值,ωk为位于功率谱密度的定义区间[ω1,ωu]内的频率。θk为均匀分布在0和2π之间的随机相位角,x为局部坐标,表示桥上某点距车辆上桥端的距离,N为模拟随机不平顺的点数。S(ωk)是功率谱密度函数,在区间[ω1,ωu]内定义为路面不平顺空间频率的函数[14]:
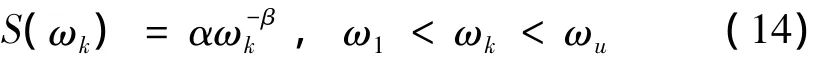
式中,指数 β 取1.94,α 是不平顺系数,见文献[16],桥上路面粗糙度可被划分为5个等级,各等级路面不平顺系数α见表2。
1.4 车桥耦合振动分析
假设车辆在行驶过程中与桥面一直接触,车轮与桥面相互作用力可以表示为:
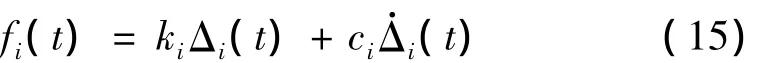
式中,下标i表示第i个车轮与桥面接触点;Δi(t)为第i个车轮t时刻相对于桥面的垂直位移,其表达式为:
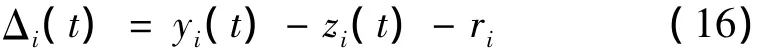
式中,yi(t)为第i个车轮t时刻的竖向位移,zi(t)为桥面t时刻在第i个车轮与桥面接触点处的竖向位移,ri为第i个车轮与桥面接触点处的桥面不平顺样本值。
车辆与桥梁作为两个子系统,其动力方程通过车轮与桥面接触点处位移相同、相互作用力大小相等耦合起来。由于车辆与桥梁之间的相互作用力与车辆的运动状态以及桥梁的变形都有关,因此需要迭代求解这两组耦合的、时变的二阶微分方程组。
本文采用Newmark-β法,基于matlab语言编制了车桥耦合振动分析程序VBAP,计算流程如图2所示。

图2 车桥耦合振动分析流程图Fig.2 Simulation procedure of vehicle-bridge coupled vibration
1.5 冲击系数
[17]中冲击系数μ的定义,将吊杆应力冲击系数定义为:

其中,σdmax为动力分析时吊杆应力最大值,σsmax为静力作用下吊杆应力最大值。
2 算例分析
2.1 分析模型
以某钢管混凝土拱桥为例分析公路车辆动力作用下的吊杆冲击系数的不均匀性问题。该桥主桥为单跨88 m下承式钢管混凝土系杆拱桥,横桥向设二片拱肋。计算跨径86 m,矢高21.5 m,矢跨比1/4,拱轴线为m=1.0的悬链线。桥梁结构主要由钢管混凝土拱肋、预应力混凝土系梁、端横梁、中横梁、吊杆及桥面板组成,总体布置如图3所示。

图3 拱桥总体布置图(单位:cm)Fig.3 The overall drawing of the arch bridge(Unit:cm)
利用通用有限元软件ANSYS建立二维有限元模型。拱肋与主梁均采用梁单元模拟,吊杆采用杆单元模拟。其中,对于拱肋部分,采用组合梁单元模拟钢管与混凝土。模型边界条件为:左端固定铰支座,右端滑移支座。整个模型共703个单元,516个节点。
2.2 分析结果
2.2.1 结构自振特性分析
运用ANSYS对上述下承式吊杆拱桥进行模态分析,前四阶自振频率及振型描述如表3所示。前四阶振型如图4所示。

表3 桥梁前四阶自振频率及振型描述Tab.3 The first 4 natural frequencies and mode shapes description of the bridge

图4 桥梁前四阶振型Fig.4 The first 4 mode shapes of the bridge
该桥一阶自振频率为 1.42Hz,根据规定[17],该桥的冲击系数应取为0.05。
2.2.2 车桥耦合振动对比分析
用自编的车桥耦合振动分析程序VBAP对20 t车以70 km/h的速度过桥进行了分析,分析中假设桥面绝对光滑。作为对比,在ANSYS中将车辆简化为移动荷载模型,用瞬态分析对该过程进行了数值模拟。两种分析方法所得1#吊杆应力时程曲线与静力分析所得1#吊杆应力如图5所示。由图5可见,结构在移动荷载模型作用下,1#吊杆的应力时程曲线只是在静力影响线的基础上有所偏移。两轴车辆模型作用下分析得到的1#吊杆应力最大值分别是静力荷载作用下应力最大值和移动荷载作用下应力最大值的1.13倍和1.2倍。移动荷载模型作用下,1#吊杆应力幅为6.23 MPa,而两轴车辆模型作用下,1#吊杆应力幅达到8.0 MPa,分别是移动荷载模型作用下应力幅和静力分析下应力幅的1.28倍和1.21倍。因此,即使不考虑路面不平顺的影响,简单的把车辆简化为移动荷载模型进行分析所得到的结果偏小,是不可靠的。

图5 1#吊杆应力Fig.5 The stress of the 1#suspender

图6 单车总轮压荷载Fig.6 Summation of reaction forces of tires
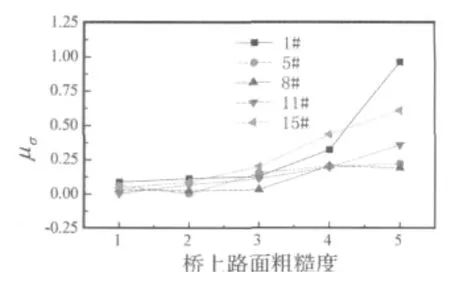
图7 路面粗糙度对冲击系数的影响Fig.7 Impact factors varying with road roughness
2.2.3 轮压荷载放大效应
为了分析车桥耦合振动对轮压荷载产生的放大效应,计算了20 t车以80 km/h的速度在三种粗糙度等级桥面下过桥,车辆总轮压荷载的变化情况,结构阻尼比设为0.02,得到的单车总轮压荷载如图6所示。结果显示,总轮压荷载静力值为常数196 kN,随着路面粗糙度增大,轮压荷载的振幅也跟着增大,在粗糙度等级为“差”条件下,轮压荷载达378.7 kN,超过静态轮压93%。
2.2.4 吊杆冲击系数不均匀性分析
为分析不同位置吊杆冲击系数的不均匀性,选取分别位于桥梁端部、1/4 跨、跨中、3/4 跨的1#、5#、8#、11#、15#吊杆作为研究对象。在下文的分析中,车辆均以匀速自左向右通过桥梁。
2.2.4.1 桥上路面粗糙度对吊杆应力冲击系数的影响
为了比较不同路面粗糙度对冲击系数的影响,分析五种等级路面下,20 t汽车以80 km/h通过该桥时桥梁结构的动力响应,结果如图7所示。
由图7可见,5根吊杆的应力冲击系数在路面粗糙度等级为“较好”或者更差时均高于我国规范中对该桥冲击系数的取值。吊杆应力冲击系数随着路面粗糙度增大而增大。以“一般”路面粗糙度等级为分界线,路面退化到“一般”以下对吊杆应力冲击系数的影响迅速增大。路面粗糙度由“一般”退化到“很差”,跨中的8#吊杆应力冲击系数增大了0.16,而1#吊杆应力冲击系数增大了0.83,是8#吊杆应力冲击系数增幅的5.2倍。因此,路面的退化、路面粗糙度的增大对短吊杆的影响要大于对跨中附近吊杆的影响。所以,运营中维持该桥路面平整可以有效降低短吊杆所受车辆荷载冲击作用,延长其使用寿命。
2.2.4.2 车速及车重对吊杆应力冲击系数的影响
为了分析车速及车重对冲击系数的影响,计算了15 t、20 t和30 t三种重量的汽车分别以30~120 km/h的速度通过该桥,路面粗糙度为一般,桥梁结构阻尼比取0.02,计算结果如图8所示。随着车速的增大,5根吊杆的应力冲击系数总体都呈减小趋势。因此,车辆以较高的车速通过可使吊杆受到较小的冲击作用。当三种重量的车辆都以60 km/h以上的速度过桥时,1#、15#端部短吊杆应力冲击系数变化幅度在0.5左右,1/4跨5#吊杆与3/4跨11#吊杆应力冲击系数变化幅度在0.3左右,跨中8#吊杆应力冲击系数变化幅度为0.16。因此,相比较而言,在桥梁的运营期间,端部短吊杆的应力冲击系数变化幅度最大,对车重的变化最敏感。另外,车重增加会使吊杆应力冲击系数有所降低。这可以通过车辆质量的增加会增大车辆的惯性,从而使车辆行驶更稳定,对结构冲击作用较小来解释。

图8 不同车重及车速下吊杆应力冲击系数Fig.8 Stress impact factors of suspenders varying with vehicle speed and weight
2.2.4.3 结构阻尼对吊杆应力冲击系数的影响
为了分析结构阻尼对挠度冲击系数的影响,计算了路面粗糙度等级为一般时,20 t车以80 km/h的速度过桥,桥梁结构阻尼比为 0.01、0.02、0.03 三种情况下的吊杆冲击系数,结果如图9所示。当结构阻尼比由0.01升至0.02,除5#吊杆外其他4根吊杆冲击系数都有不同程度的下降。其中,以15#吊杆应力冲击系数下降了60%,变化幅度最大。但是,当结构阻尼比由0.02升至0.03时,5根吊杆应力冲击系数都有所上升,上升幅度最大的仍是15#吊杆,上升了45%。因此,单纯的增大结构阻尼比并不能减小吊杆应力冲击系数,而是存在一个最优的阻尼比使吊杆受到的冲击作用最小。另外,与其他位置处的吊杆相比,桥梁两端的短吊杆对结构阻尼的变化更敏感。

图9 桥梁结构不同阻尼比下冲击系数Fig.9 Impact factors varying with damping ratio of bridge
3 结论
(1)车桥耦合振动对轮压荷载具有放大效应。
(2)路面的退化、路面粗糙度的增大对桥梁端部短吊杆的影响要大于对跨中附近吊杆的影响,路面退化到“一般”以下对吊杆应力冲击系数的影响迅速增大,运营中维持该桥路面平整可以有效降低短吊杆所受汽车荷载冲击作用,延长其使用寿命。
(3)吊杆应力冲击系数随车速增大而减小,使车辆以较高的车速通过该桥可使吊杆受到较小的冲击作用。
(4)端部短吊杆对车重的变化最敏感,空车过桥比满载车辆过桥所产生的冲击系数更大。
(5)单纯的增大结构阻尼比并不能减小吊杆应力冲击系数,而是存在一个最优的阻尼比使吊杆受到的冲击作用最小。与其他位置处的吊杆相比,桥梁两端的短吊杆对结构阻尼的变化更敏感。
参考文献
[1]朱劲松,邑 强.拱桥新型吊杆安全性及其静动力影响研究[J].桥梁建设,2011,1:39-42,51.
[2]李小珍,张黎明,张 洁.公路桥梁与车辆耦合振动研究现状与发展趋势[J].工程力学,2008,25(3):230-240.
[3]Huang D Z.Dynamic and impact behavior of half-through arch bridges[J].Journal of Bridge engineering,2005,10(2):133-141.
[4]王解军,张 伟.汽车荷载作用下梁桥的动力冲击效应研究[J].振动与冲击,2007,26(6):125-128.
[5]殷新锋,方 志.车辆作用下开裂混凝土连续梁桥的动力响应分析[J].工程力学,2009,26(4):174-180.
[6]崔圣爱,祝 兵,白峰涛,等.琼洲海峡跨海斜拉桥方案车桥系统耦合振动仿真分析[J].振动与冲击,2011,30(5):106-110.
[7]黄新艺,陈彦江,李 岩,等.曲率半径对曲线箱梁桥车辆荷载作用下冲击效应的影响[J].振动与冲击,2010,29(1):38-42.
[8]Bruno D,Greco F,Lonetti P.Dynamic impact analysis of long span cable - stayed bridges under moving loads[J].Engineering Structures,2008,30(4):1160 -1177.
[9]Lei G,Moe S C.Computer simulation of dynamic interactions between vehicle and long span box girder bridges[J].Tsinghua Science and Technology,2008,13(S1):71-77.
[10]Hamidi S A,Danshjoo F.Determination of impact factor for steel railway bridges considering simultaneous effects of vehicle speed and axle distance to span length ratio[J].Engineering Structures,2010,32(5):1369 -1376.
[11]Wu S Q,Law S S.Dynamic analysis of bridge with non-Gaussian uncertainties under a moving vehicle[J].Probabilistic Engineering Mechanics,2011,26(2):281-293.
[12]Wu S Q,Law S S.Dynamic analysis of bridge-vehicle system with uncertainties based on the finite element model[J].Probabilistic Engineering Mechanics,2010,25(4):425-432.
[13]Leitao P N,Silva J G S,Vellasco P C G D,et al.Composite(steel-concrete)highway bridge fatigue assessment[J].Journal of Constructional Steel Research,2011,67(1):14-24.
[14]Honda H,Kajikawa Y,Kobori T.Spectra of road surface roughness on bridges[J].Journal of structural division ASCE,1982,108(ST9):1956-1966.
[15]Au F T K,Cheng Y S,Cheung Y K.Effects of random road surface roughness and long-term deflection of prestressed concrete girder and cable-stayed bridges on impact due to moving vehicles[J]. Computers and Structures,2001,79(8):853-872.
[16]ISO 8608. Mechanical vibration-road surface profiles reporting of measured data[S].ISO,1995.
[17]中交公路规划设计院.JTG D60-2004公路桥涵设计通用规范[S].北京:人民交通出版社,2004.
