谱函数的渐近表达式

崔庆岳

(广州城建职业学院 基础部，广州 510925)

谱函数的渐近表达式

崔庆岳

(广州城建职业学院 基础部，广州 510925)

一端奇异Sturm-Liouville方程在满足Neumann边条件下相对应的谱函数的一种渐近表达形式，其中方程在奇异点属于极限点型．

Sturm-Liouville方程;谱函数;渐近表达式;极限点型

1 概述及预备知识

考虑当λ=u()＞0的微分方程

满足初始条件

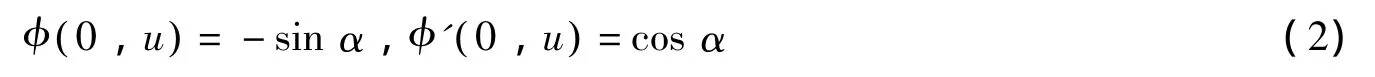
的解φx，()u，其中参变量q∈L0，()∞。由常数变易法可得方程的解，如下所示

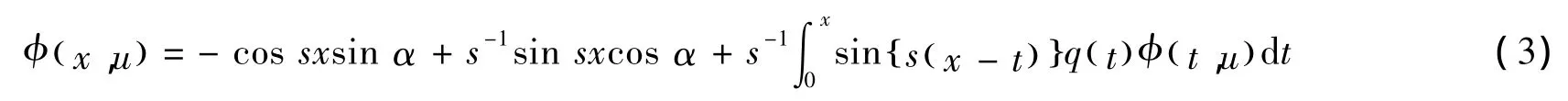
其中u=s2。如文献［1］所示，当q∈L 0，()∞时，存在函数()a u和()b u使得

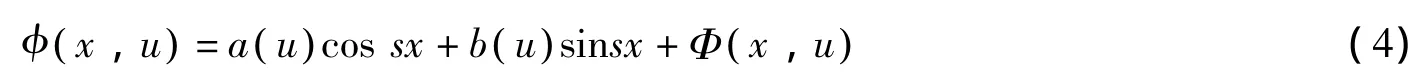
成立。其中()a u和()b u是与变量x线性无关的函数，并且当x→∞时，Φ x，()u→0。Coddington在文［2］中证明了谱函数可以通过函数 ()a u和 ()b u来表示，即

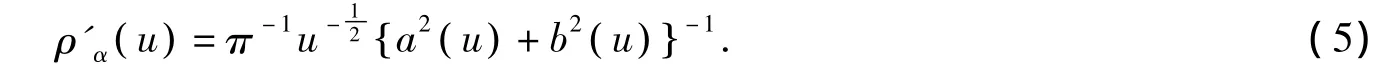
因此，当u→∞时，确定方程(1)的解φ x，()u的渐近形式，近而求出函数()a u和()b u的表达式，然后再利用上式求得谱函数的渐近表达式。

引理1［3］设()ρ λ为谱函数，λ1，λ2为它的任两个连续点，M()λ为对应的Weyl函数，则

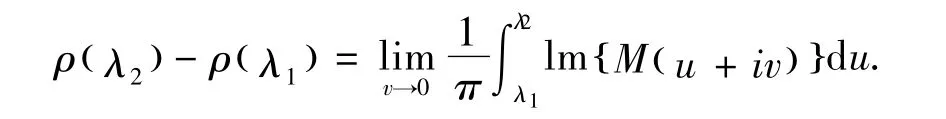
2 谱函数的渐近表达式

一端奇异Sturm-Liouville方程

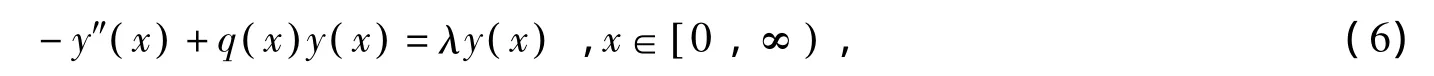
满足初始条件

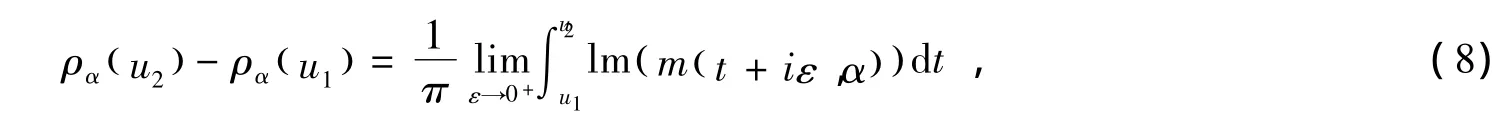
其中()q x在区间0，[)∞上为局部可积的实函数，α为实数。

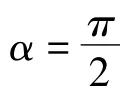
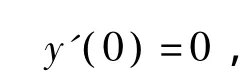
即为方程 (6)的Neumann边条件。

主要讨论一端奇异Sturm-Liouville方程 (6)在满足Neumann边条件下，当参变量q满足一定条件及u→∞时谱函数的一种渐近表达形式，其中方程 (6)在奇异点∞属于极限点型。

首先，讨论当u→∞时函数 ()a u和 ()b u的渐近表达式，近而推得谱函数的渐近形式。

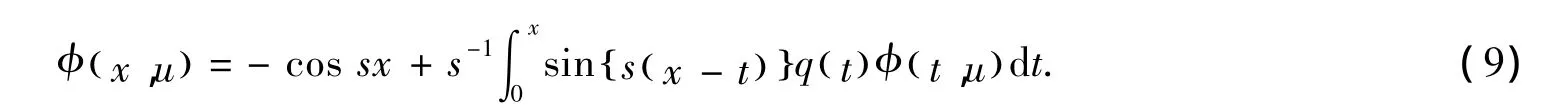
为了将上式展开，下面在区间0，[)∞上引入函数列Bk()x，设B1()x=－1，

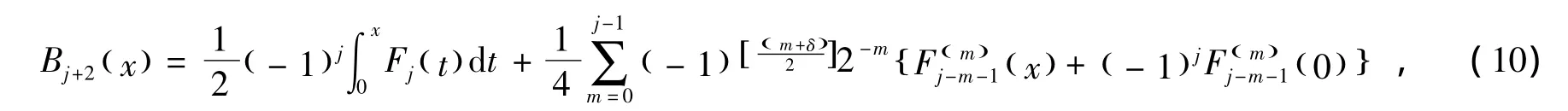
其中j≥0，当j为偶数时，δ=0;当j为奇数时，δ=1。［·］表示取其整数部分。并且

由 (10)式和 (11)式可得

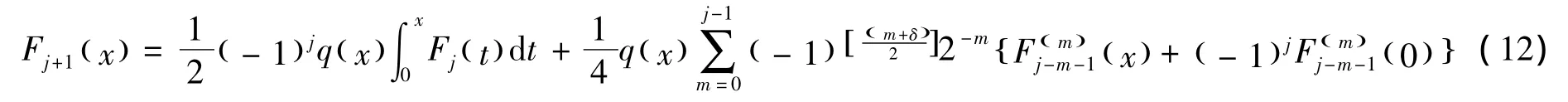
其中

由(12)式可得

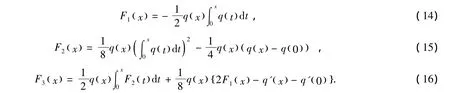
和

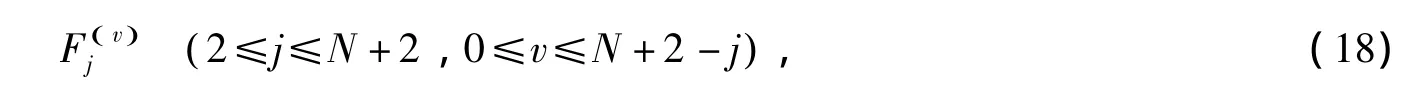
都属于空间L 0，()∞。

由上述引理可知，存在 (17)式和 (18)式的一个序列

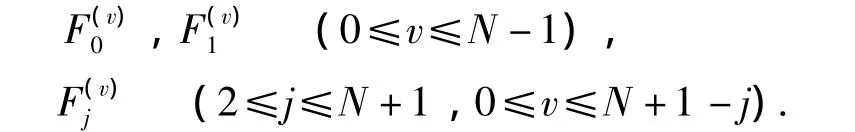
使得当x→∞时，上述函数列都可以表示成o()1，则 (10)式有下列表示形式

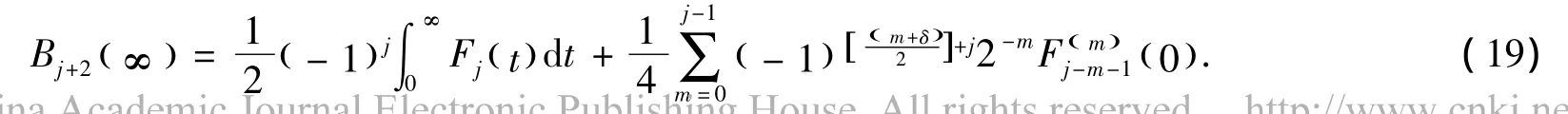
因此，结合 (11)式和 (14)－(16)式可得

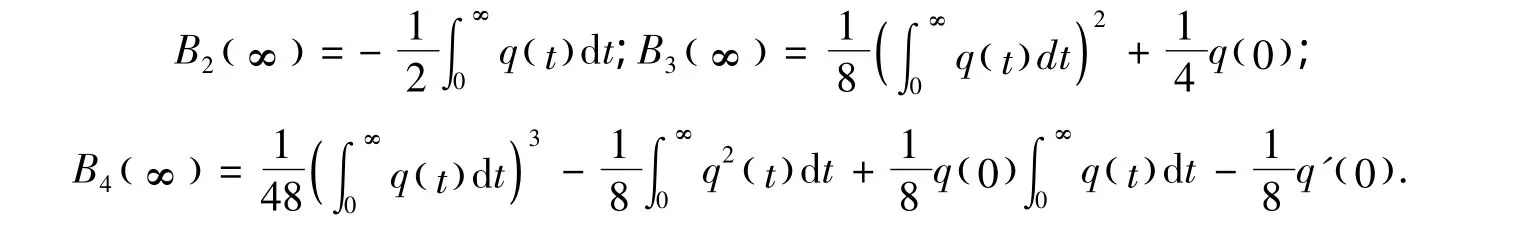
下面的定理将给出方程解φ x，()u的另外一种渐近表达形式，从而把(4)式和(5)式联系起来。

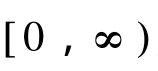
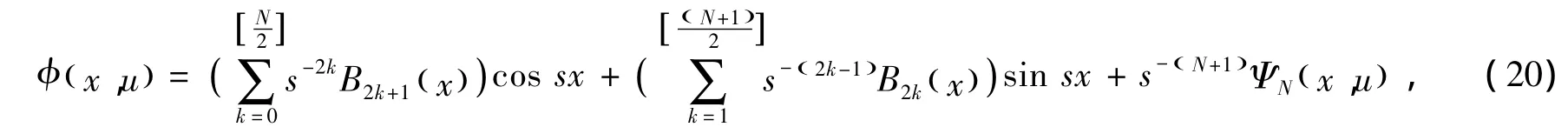
其中

并且当0≤x＜∞和s≥s0＞0时，KN是与参变量x和s线性无关的常数。

证明 由(9)式可得

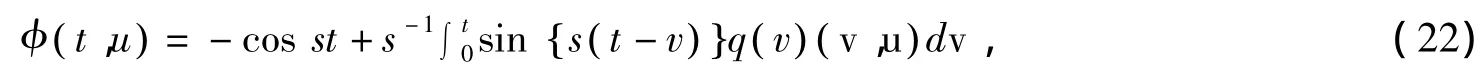
将(22)式代入到(9)式中的积分项，并进行整理可得

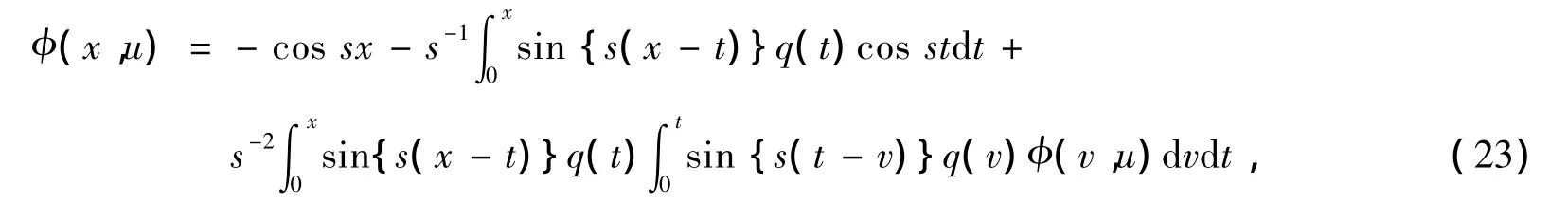
将(23)式展开，并且由(10)式和(11)式可得

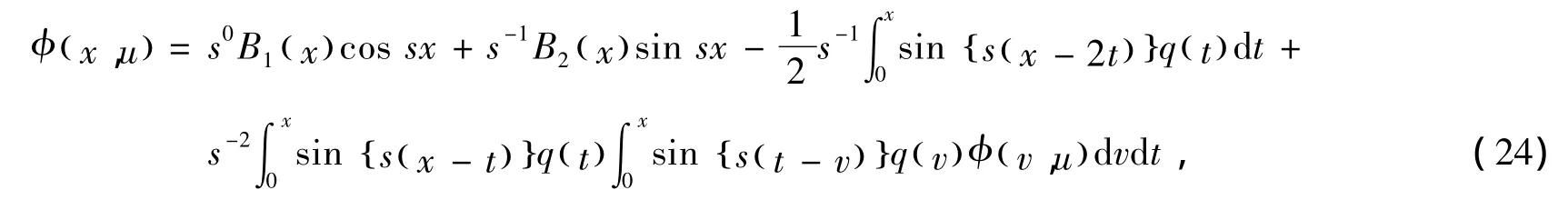
因此，再对 (24)式进行重复迭代N－1次就可得 (20)式。下面重点给出 (21)式的证明。设SN()x和CN()x分别表示 (20)式中函数sin sx和cos sx前的函数项，即

由 (9)式可得，S0()x=0，C0()x=－1，再由Cronwall不等式［1］可得

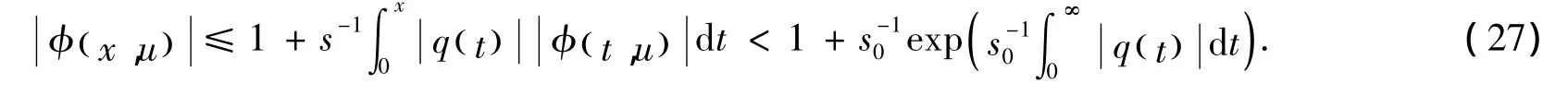
令

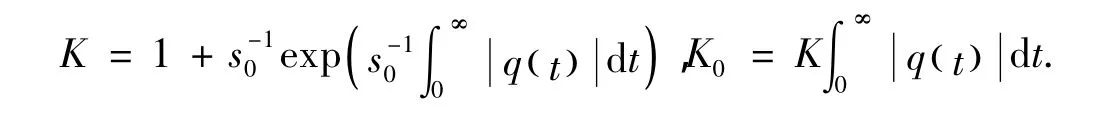
因此，

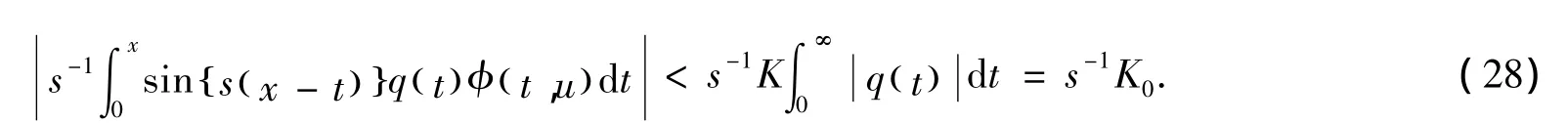
这就证明了当N=0时的情形。下面假设N－1次展开式 (20)和不等式 (21)均成立，证明N次展开式和不等式也成立。将N－1次展开的 (20)式代入到 (9)式中的积分项，并进行整理可得

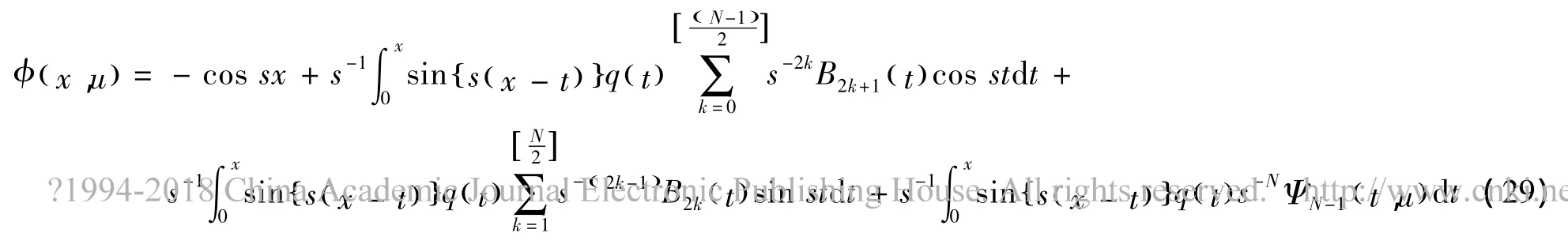
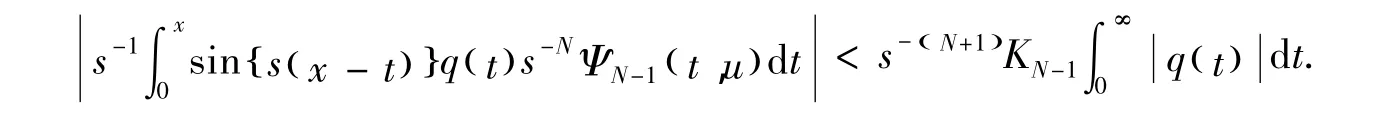
首先，对 (29)式的最后一项进行渐近估计可得显然上式符合 (21)式的估计形式，并且构成KN的一部分。下面考虑 (29)式的第二项，因为上式等号右侧第一项可归为SN进行估计，对上式等号右侧的第二项进行N－2k次分部积分并取最后一个积分项，即含s－N( )由此可知，下面不等式成立+1的系数项，表示如下再根据 (11)式和引理1可得，上式是收敛的。因此可得，其估计式也符合 (21)式，同样构成KN的一部分。利用相同的方法，可证得包含SN－1的积分项也符合估计式 (21)。因此可证得，对于所有的x∈0，[)∞和s≥s0≥0都有(21)式成立。

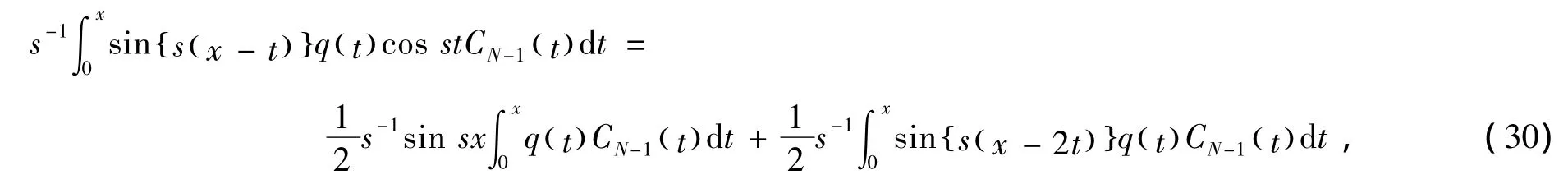
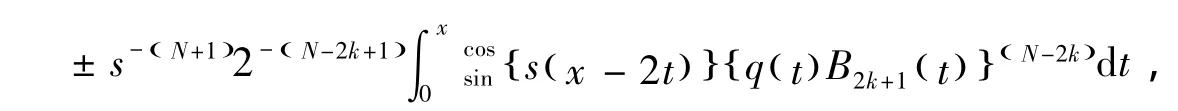
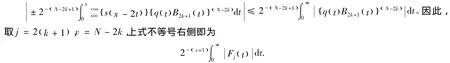
定理3 假设qN( )－1在区间0，[)∞是局部绝对连续的，并且q()v∈L 0，()∞，其中0≤v≤N(N是

正整数)，则当u→∞时，

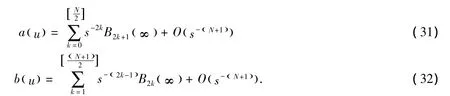
证明 由于 (4)式和 (20)式是方程 (6)的解的两种不同表达形式。因此，对于任意固定的s，令 (4)式和 (20)式相等，即

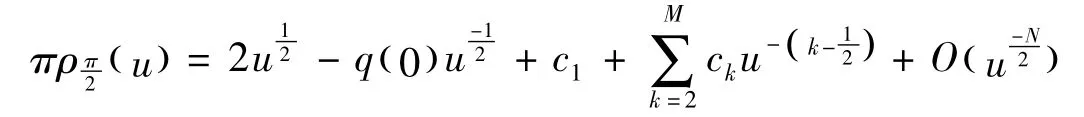
成立，在此［·］表示取整数部分。

证明 由定理3可得

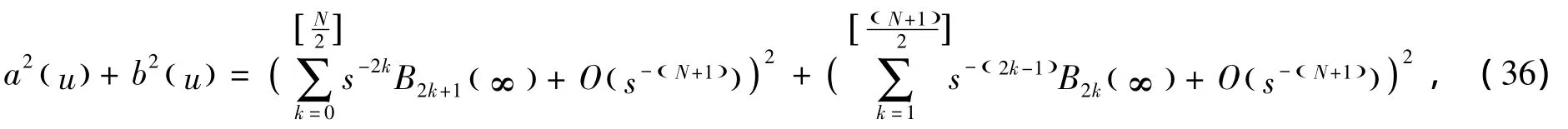
对(36)式进行整理可得

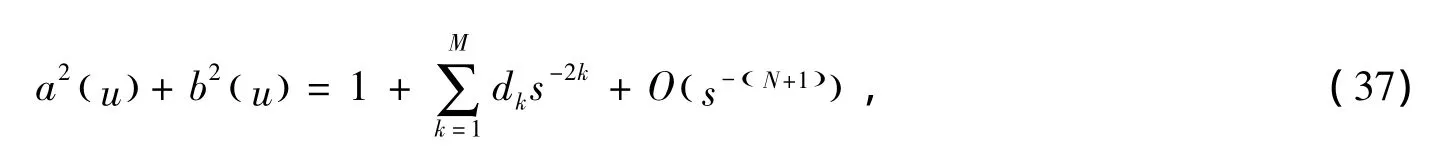
其中dk是常数，特别的，由 (19)式和 (37)式可得

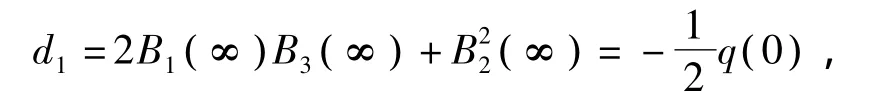
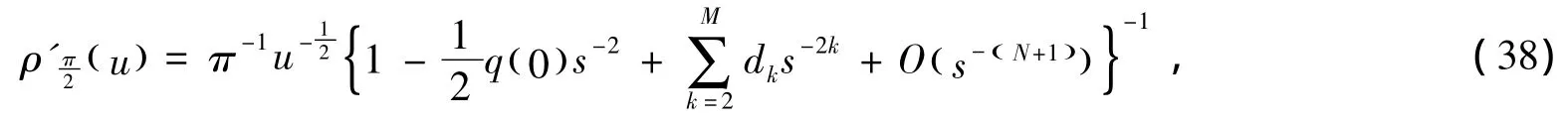
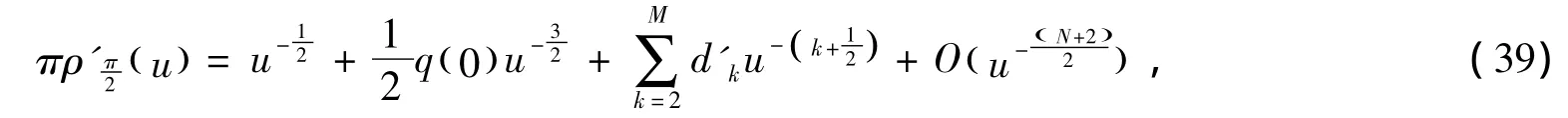
其中d'k为常数，对 (39)式进行积分可得

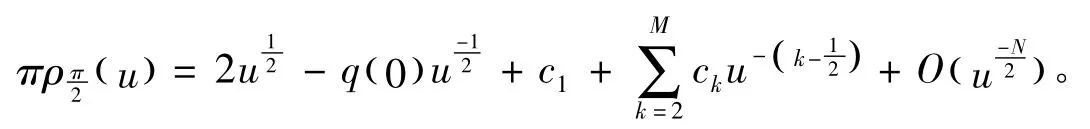
因此证得定理成立。

［1］Titchmarsh E C．Eigenfunctions Expansions Associated With Second Order Diffetential Equations：vol I［M］．2nd ed．London：Oxford Univ Press，1962．

［2］Coddington E A，Levinson N．On the nature of the spectrum of singular，second order linear differential equations［J］．Canad J Math，1951(3)：335－338．

［3］曹之江．常微分算子［M］．上海：上海科学技术出版社，1987．

［4］Coddington E A，Lvinson N．Theory of Ordinary Differential Equations［M］．New York：McGraw-Hill，1955．

［5］Eastham M S P．The asymptotic nature of spectral functions in Sturm-Liouville problems with continuous spectrum［J］．J Math Analysis Appl 1997，213：573－582．

The Asymptotic Expression of the Spectral Function

CUI Qing-yue
(Guangzhou City Construction College，Guangzhou 510925，China)

The asymptotic expression form of the spectral function correspond to the Sturm-Liouville equation which satisfy Neumann boundary conditions at one singular endpoint．

Sturm-Liouville equations;spectra function;asymptotic expression;limit point

O175.3

A

1009－0312(2012)01－0019－05

2011－04－20

崔庆岳 (1984—)，男，山东济宁人，硕士，主要从事微分算子及其谱分析研究。