简单互联电力系统的跳跃现象与共振行为

罗晓华 何为

(1．重庆交通大学 图书馆，重庆 400074;2．重庆大学 电气工程学院，重庆 400044)

简单互联电力系统的跳跃现象与共振行为

罗晓华1，2何为2

(1．重庆交通大学 图书馆，重庆 400074;2．重庆大学 电气工程学院，重庆 400044)

在小振幅近似下，把电力系统的控制方程化为了经典的Duffing方程，用Jacobian椭圆函数和第一类椭圆积分解析地给出了无扰动系统的周期解，并用摄动法分析了扰动系统在共振线附近的运动行为;揭示了系统的跳跃现象与不稳定性。结果表明，只需适当选择系统的工作状态 (比如，尽量远离共振线)，系统就是稳定的。

电力系统;共振;跳跃现象;稳定性;Duffing方程

电力系统是一个典型的非线性系统，非线性系统的稳定性问题是倍受关注的问题之一［1－5］。比如，电力系统在遭受周期性负荷扰动时，系统就可能会发生混沌振荡［6－7］;工作在共振线附近时，可能会出现跳跃现象。混沌振荡已成为电力系统稳定性研究的重要课题，其中包括平衡态失稳及失稳后的周期振荡问题;而跳跃将产生电频率突变，导致系统不稳定。事实上，电力系统的混沌振荡、电压崩溃和频率崩溃是导致电网事故的三大主要原因。

本文就对后一个问题进行讨论。首先，从电力系统的广义的摆方程出发，在小振幅近似下把电力系统的控制方程化为了经典的Duffing方程;其次，用Jacobian椭圆函数和第一类椭圆积分解析地给出了无扰动系统的周期解，并用摄动法分析了扰动系统在共振线附近的运动行为［8－9］;揭示了系统的跳跃现象与不稳定性。结果表明，只需适当选择系统的工作状态 (比如，尽量远离共振线)，系统是稳定的。

1 系统的摆模型

注意到最重要的工程问题之一是它的物理模型。由于认识都是近似的，人们就在不同的近似下提出了不同模型对对工程问题进行描述，电力系统也不例外。其中简单互联的电力系统模型是一个用得最多、最广的物理模型之一。图1给出了简单互联电力系统示意图。

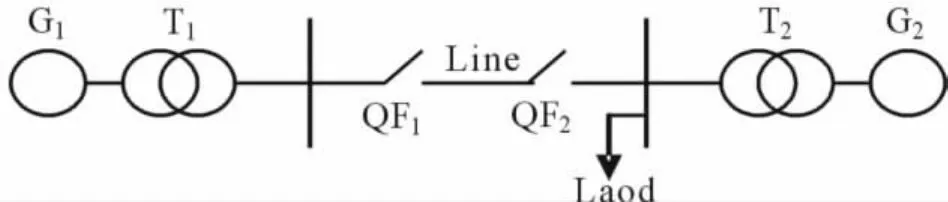
图1 简单互联的电力系

在一定假设下，具有周期负荷扰动的简单互联电力系统 (见图1)的可化为如下形式的数学问题：

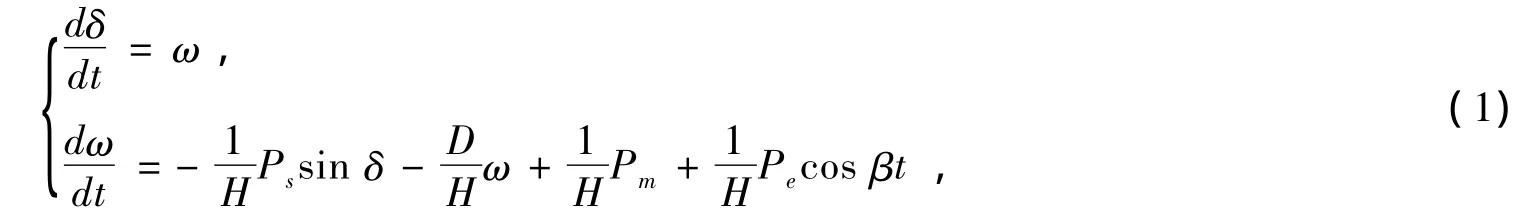
其中δ为发电机转子运行角;ω为发电机相对转速;Pm，Ps分别为发电机机械功率和电磁功率;H为等值转动惯量;D为等值阻尼系数;Pe为扰动功率幅值;β为扰动功率变化频率。令

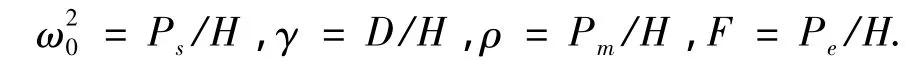
方程 (1)可进一步化为

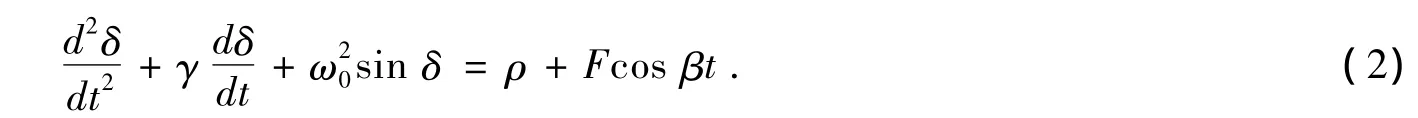
方程 (2)是一个广义的摆方程，也是一个典型的动力学系统，存在着复杂的分叉与混沌现象;在小振幅近似下，还存在共振行为与跳跃现象。鉴于方程 (2)不存在严格的解析解，我们在小振幅近似下，把粒子运动方程化为具有硬弹簧特性的Duffing方程，用摄动法求出系统的近似解，并分析了共振线附近粒子的运动行为和系统的跳跃现象。

在小振幅近似下，假设平衡相位δ0=ρ/ω20比较小，方程 (2)可化为

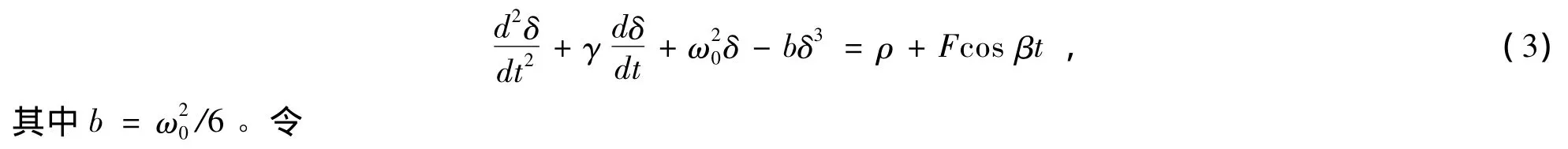
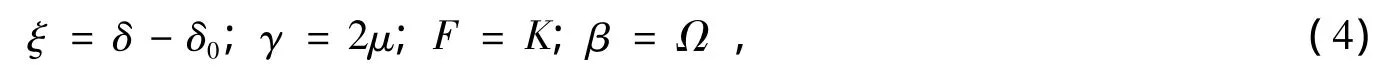
方程 (3)可化为

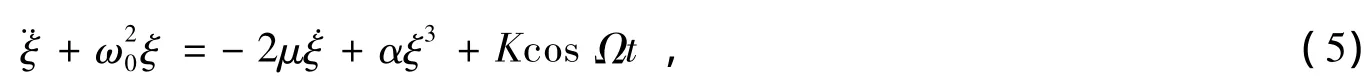
字母上方的圆点表示对时间t的微商。方程 (5)是一个经典的Duffing方程。

2 简单互联的电力系

为了表示方程 (5)中各项的大小，我们引入小参数ε。如果系统 (5)中的受迫项大小为O(ε)量级时，系统将存在Ω=ω0的主共振。其中ε是小量。为此，我们假设方程(5)中的2μ˙ξ，αξ3和Kcos Ωt项的大小是O(ε)数量级，其他项是O(1)数量级，则形式上可将方程 (5)改写为

(式中ε只表示该项大小，只需在结果中令ε=1即可回到原来状态)。

如果不考虑扰动 (ε=0)，系统是一个哈密顿系统。它的等价系统可表示为

相应的的哈密顿量

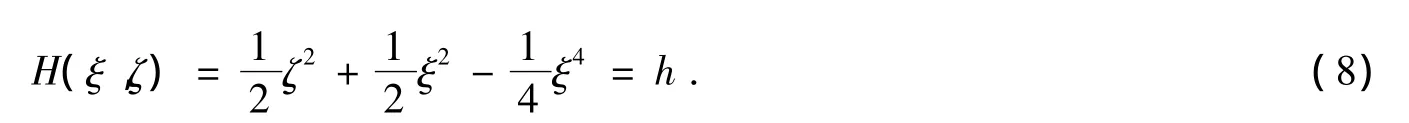
从式 (8)可以看出，在相平面上，(0，0)是系统 (7)的一个中心，而另外两点(1，0)和(-1，0)是它的鞍点。当0＜h＜1/4，存在一族围绕中心(0，0)的周期轨道，

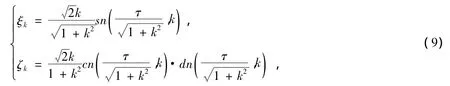
其中sn(u)，cn(u)，dn(u)是雅可比椭圆函数，k是椭圆函数的模 (0＜k＜1)，相应的轨道周期可表示为?

周期轨道是椭圆轨道，对应于系统绕平衡位置 (ξs=0)的周期运动;在平衡点附近，相轨线近似为一个圆。

3 系统的稳定性

3.1 摄动解

利用多重尺度法，把扰动系统 (6)的解按不同的时间尺度展开

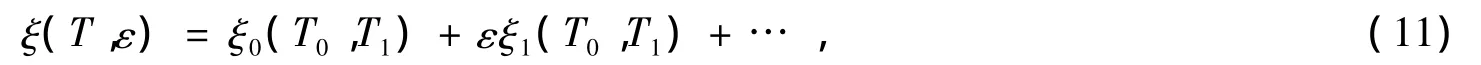
式中T0=t，T1=εt。我们关心的是系统在共振线附近 (Ω≈ω0)的运动行为，为此，引入解谐因子σ来描写粒子离开共振线的程度。于是Ω可表示为，

式中σ=O(1)，而

将式 (16)和 (18)代入式 (6)中，并分别令ε0和ε1的系数相等，可得

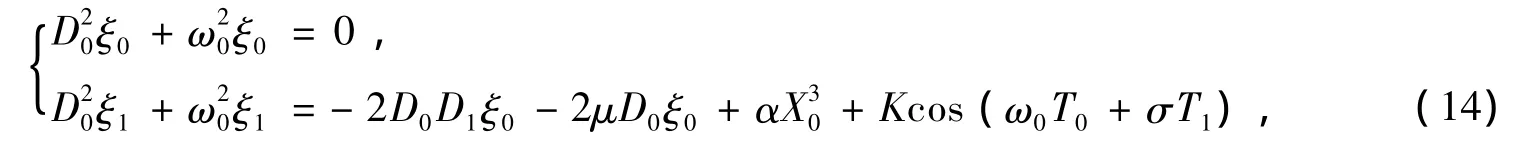
式中Dn=∂/∂Tn，解方程 (19)可得方程 (6)的一级近似解

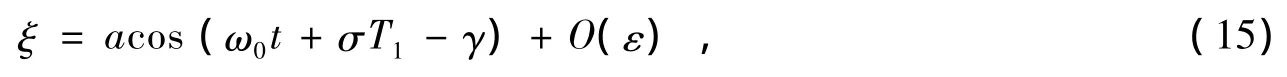
其中a和γ由方程 (16)给出。

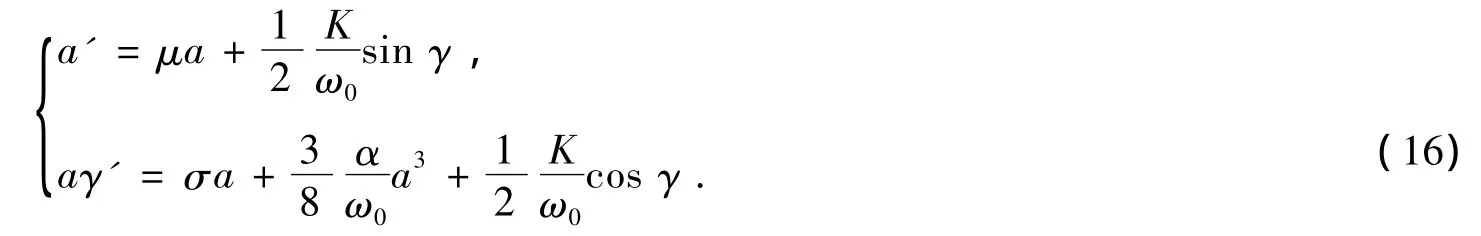
从方程 (6)、(15)和 (16)可以看出，求解二阶微分方程 (6)的问题转化为求解两个一阶微分方程 (16)的问题。但是，由于方程 (16)的右边既是a的函数，又是γ的函数，要把它积分到最终形式仍然是很困难的。不过，根据彭加勒 (Poincare)定理，不积分方程 (16)也可得到若干重要结果。比如，它的静态 (a'=γ'=0)解就十分重要。

3.2 跳跃现象

对于静态解 (a'=γ'=0)，方程 (16)化为

于是静态解可表示为

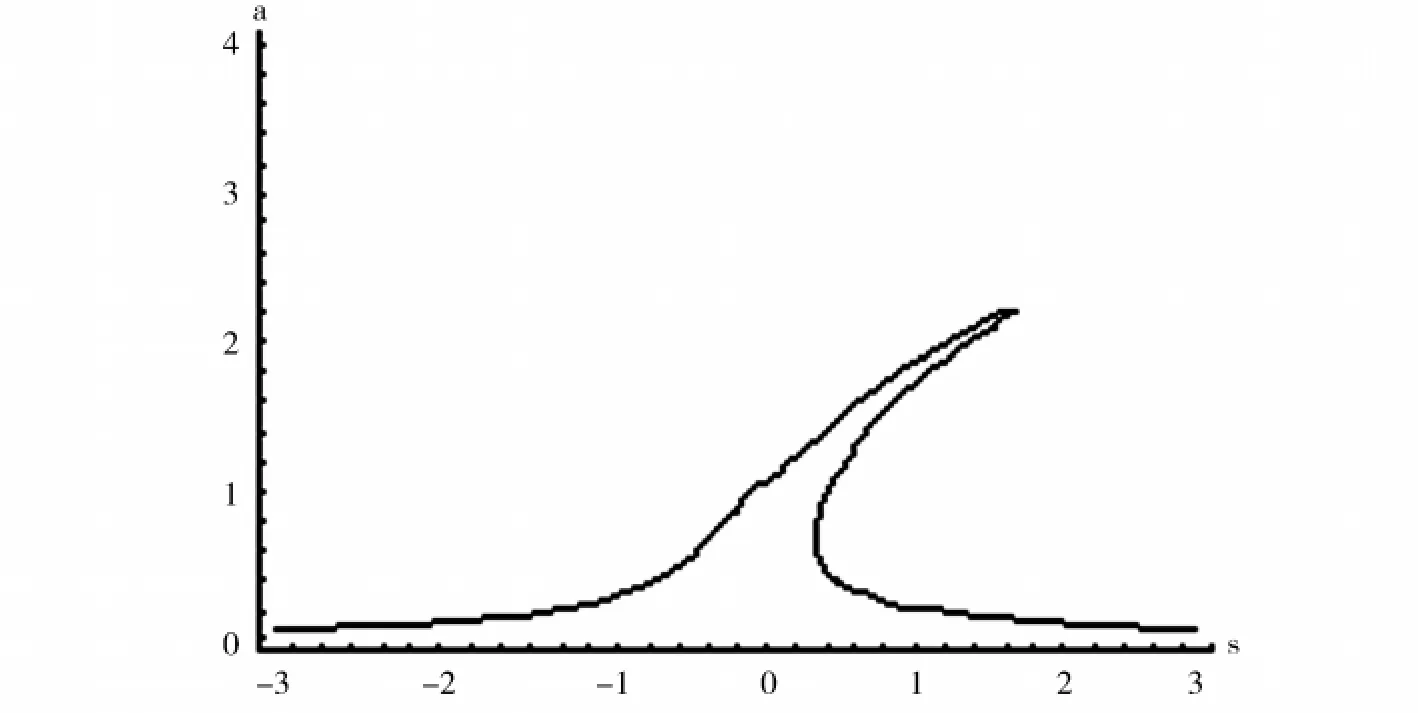
图2 系统的非线性频率响应曲线。选择参数K=0.5，μ2=0.1，α=1，ωo=1

式中a和γ由方程 (16)给出。由方程 (17)可得系统的非线性频率响应曲线 (共振曲线)

3.3 稳定性

为了讨论静态解的稳定性，令

式中a0和γ0是系统的静态解，满足方程 (16)，而a1和γ1是离开静态解的任意小量。把方程 (20)代入方程 (16)，按小量a1和γ1展开，保留线性项可得

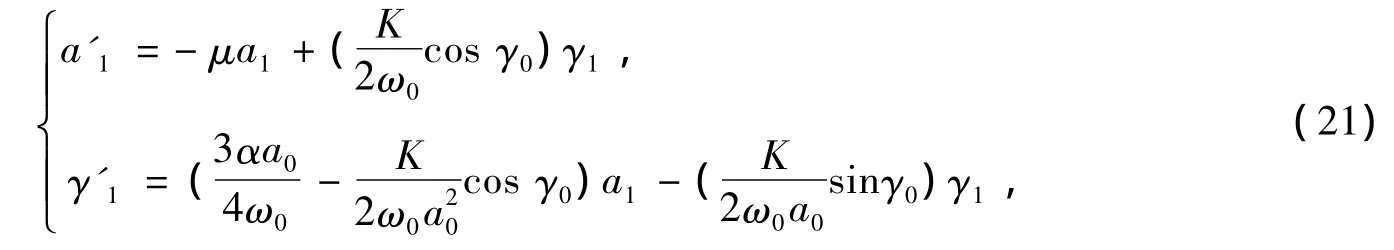
系统的稳定性与下列本征方程

的本征值有关，式中

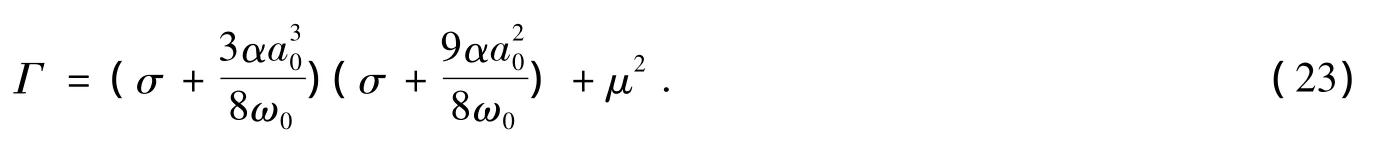
当Γ＞0时系统是稳定的;当Γ＜0时系统不稳定;当Γ=0时系统处于临界状态。

4 结论

电力系统是一个典型的动力学系统，它存在着复杂的分叉与混沌现象;在小振幅近似下，还存在共振与跳跃。比如，电力系统在遭受周期性负荷扰动时，系统就可能会发生混沌振荡;工作在共振线附近时，系统会出现跳跃现象。事实上，电力系统的混沌振荡、频率崩溃和电压崩溃是导致电网事故的三大主要原因。鉴于系统不存在严格的解析解，我们在小振幅近似下，把粒子运动方程化为具有硬弹簧特性的Duffing方程，用摄动法求出了系统的近似解，揭示了系统的跳跃现象与不稳定性。结果表明，只需适当选择系统的工作状态 (比如，尽量远离共振线)，系统是稳定的。

［1］Arjen D，Koenperink A F，Mass R M．Quasi－ periodically forced nonlinear Helmholtz oscillation［J］．Physica D，2002，164(1)：1 －27．

［2］贾宏杰，余贻鑫，王成山．电力系统混沌现象及相关研究［J］．中国电机工程学报，2001，21(7)：26－30．

［3］王宝华，杨成梧，张强．电力系统分叉与混沌研究综述［J］．电工技术学报，2005，20(7)：1－10．

［4］张强．电力系统非线性振荡研究［J］．电力自动化设备，2002，22(5)：17－19．

［5］张卫东，张伟年．电力系统混沌振荡的参数分析［J］．电网技术，2000，24(12)：17－20．

［6］王宝华，张强．电力系统振荡分叉及其稳定性分析［J］．南京工学院学报(自然科学版)，2007，5(2)：20－27．

［7］罗诗裕，邵明珠，刘曾荣，等．弯晶沟道的混沌行为［J］．物理学报，1988，37(8)：1394－1399．

［8］罗晓华，何为，邵明珠．掺杂超晶格量子阱的沟道效应与沟道辐射［J］．强激光与粒子束，2008，20(5)：812－815．

［9］罗诗裕，邵明珠，罗晓华．正弦平方势与应变超晶格位错动力学［J］．中国科学：物理学，力学，天文学，2010，40(2)：207－212．

Jumping Phenomenon and Resonance Behavior of Simple Interconnected Power System

LUO Xiao-hua1，2HE Wei2
(1．Library，Chongqing University of Communications，Chongqing 400074，China;2．Electric Engineering College Chongqing University，Chongqing 400044，China)

In the small amplitude approximation，the controlled equations of power system is reduced to the classic Duffing equation;Jacobian elliptic function and the first class of elliptic integral analytically produce the periodic solution of the perturbless system by，and the behavior of the perturbed system in the vicinity of resonance line is analyzed by using perturbation method;and the system＇s jump phenomena and instability are revealed．The results show that the system is stable under the certain conditions of the appropriately selected working status，for example，being as far as possible away from the resonance line．

power system;resonance;jump phenomena;stability;Duffing equation

TM 712;O415.5

A

1009－0312(2012)01－0044－05

2011－09－02

罗晓华 (1969—)，男，重庆人，博士生，主要从事声子同物质相互作用研究。