LTE系统PRACH基带信号的研究与实现*
2012-06-03陈发堂吴增顺
陈发堂,吴增顺
(重庆邮电大学 通信与信息工程学院,重庆 400065)
随着通信技术的不断发展,对长期演进(LTE)技术的研究不断的深入并逐渐商用,在20 MHz频谱带宽下LTE要求能够提供下行100 Mb/s与上行50 Mb/s的峰值速率。在LTE系统中,物理随机接入信道(PRACH)主要用于用户设备(UE)开始进行上行同步或者在小区之间进行切换,只有在随机接入过程完成后,UE才能和网络端进行正常的数据发送与接收,因此随机接入过程是实现LTE系统正常通信的前提和保障[1]。PRACH基带信号的生成在随机接入过程UE发送端中起着至关重要的作用,它能否高效地实现直接影响着LTE系统的整体性能。
本文通过对PRACH基带信号的研究与分析,给出了一种PRACH基带信号快速高效的实现方案[1-2],该方案主要包括:(1)频域随机接入前导的生成[3-4];(2)大素数的IDFT的快速实现方法[5]。通过理论分析与仿真,验证该方案的高效性,该方案已在TD-LTE射频一致性测试仪表中得到应用。
1 算法分析
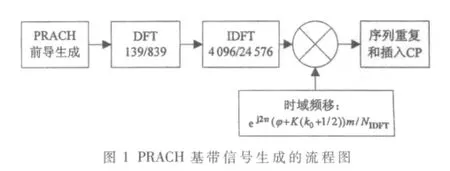
PRACH基带信号生成的流程图如图1所示。根据LTE的标准,时域上的PRACH基带信号定义为:
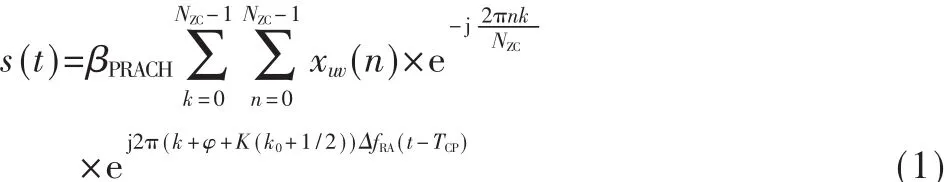
式(1)中 0≤t<TSEQ+TCP,βPRACH为幅度因子。
相关参数如表 1。 采样频率f=1/Ts,将t=iTs带入S(t),S(t)的离散形式为:
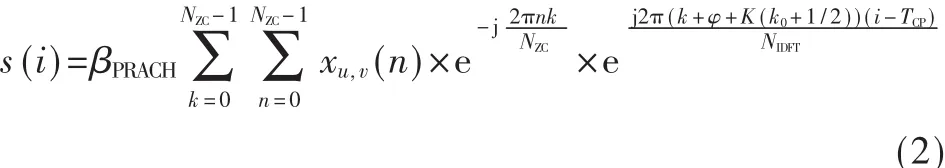

表1 随机接入基带信号的相关参数
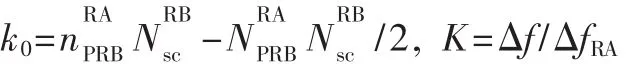
xu,v(n)=xu((n+Cv)modNZC),Cv为时域偏移量
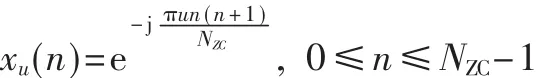
根据DFT计算公式可知式(1)中
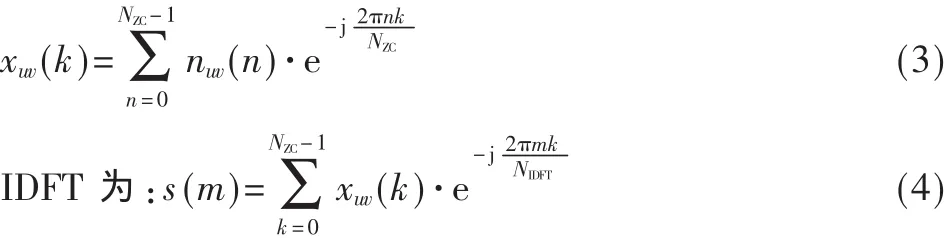
由LTE协议标准可知,采样率为1/Ts=30.72 MHz,NIDFT=1/(ΔfRATS),对于前导格式 0-3,NIDFT=24 576,对于前导格式 4,NIDFT=4 096。
对于DFT如果直接进行计算,每计算一个频域值,除了计算旋转因子的指数外,还要进行一次复数计算和NZC次的加法运算,计算量比较大,相对有效的办法就是采用快速傅里叶变换(FFT)进行计算,然而随机接入前导的长度为素数,并不能满足2的n次方的条件,无法直接采用FFT进行计算。因此需要对前导序列的DFT进行变换。
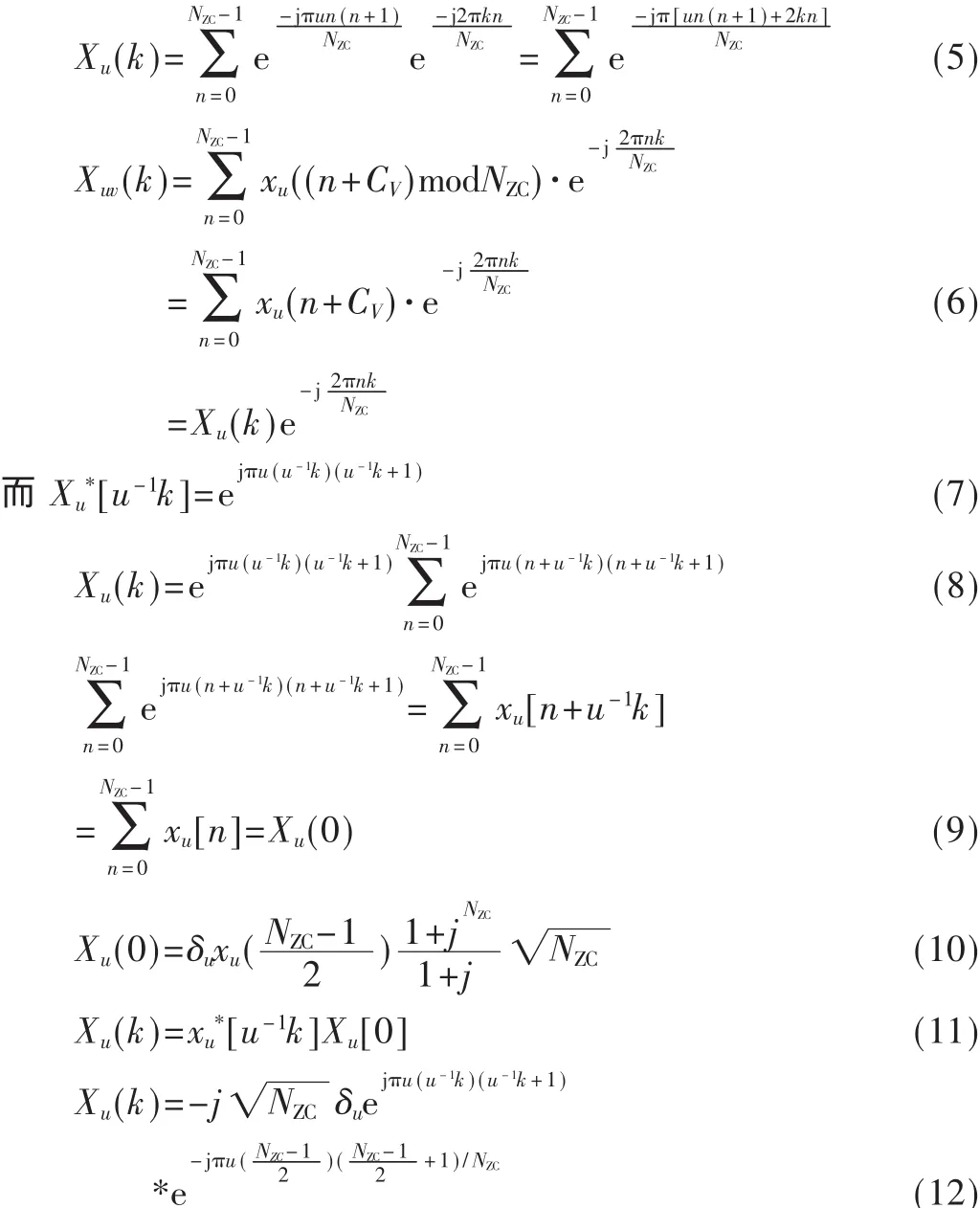
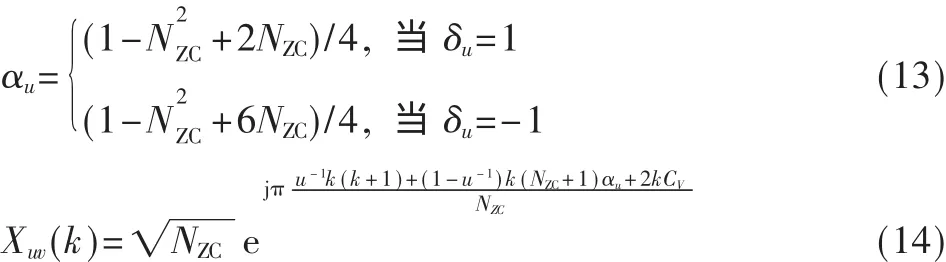
经过推导可以清楚地看出,计算每一个频域值只需要计算旋转因子的指数和做一次复数与实数的相乘,大大简化了计算的复杂度。
前导序列完成DFT计算后的长度为NZC,要进行24 576/4 096点的IDFT计算,需要在NZC点的DFT之后添加大量的0,前导格式4的IDFT运算的点数为4 096点,满足2的n次方,尚可以采用FFT进行计算。但前导格式0-3的IDFT运算的点数为24 576点,点数极大,且不能直接采用FFT进行处理。因此对24 576点的IDFT需要做一些处理。其中一种行之有效的方法就是:将大点数的IDFT分成若干个小的长度,且分成的长度较小点均能满足2的n次方,可以采用FFT进行处理。令m=aM+b,其中M=NIDFT/NIFFT为总组数,a=0,1,2…NIFFT-1为每一组中的索引指数,b=0,1,2…M-1为组的索引指数。
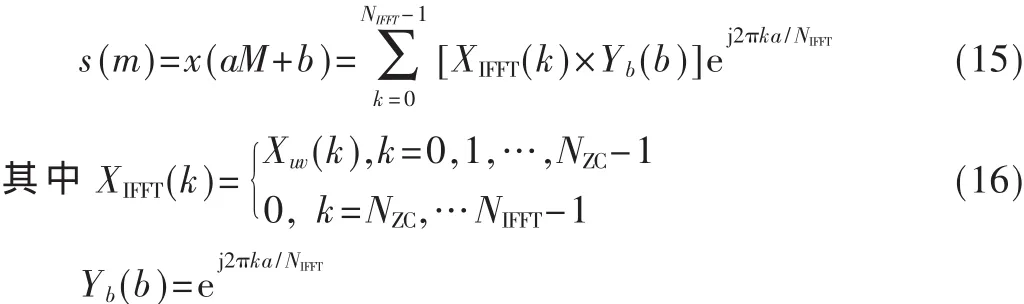
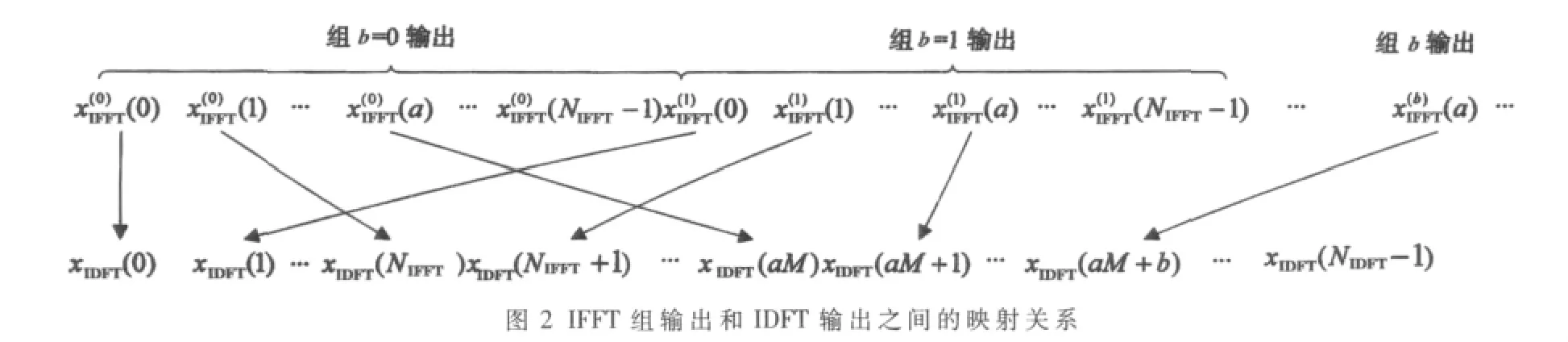
以前导格式 0-3为例,NZC=839,将NIDFT=24 576分成24组NIDFT=1 024点的IFFT进行计算,因为NIFFT=1 024点的 IFFT最接近NZC=839点,而且 1 024点的 IFFT可以采用基2或基4的IFFT进行实现。IFFT组输出与IDFT输出之间的映射关系如图2所示。
根据表2可以看出只有在前导格式3和4时,需要进行前导序列的重复,其他情况均无前导的重复。
设m=i-Tcp,m1=m+NIDFT,则有:

表2 随机接入前导参数
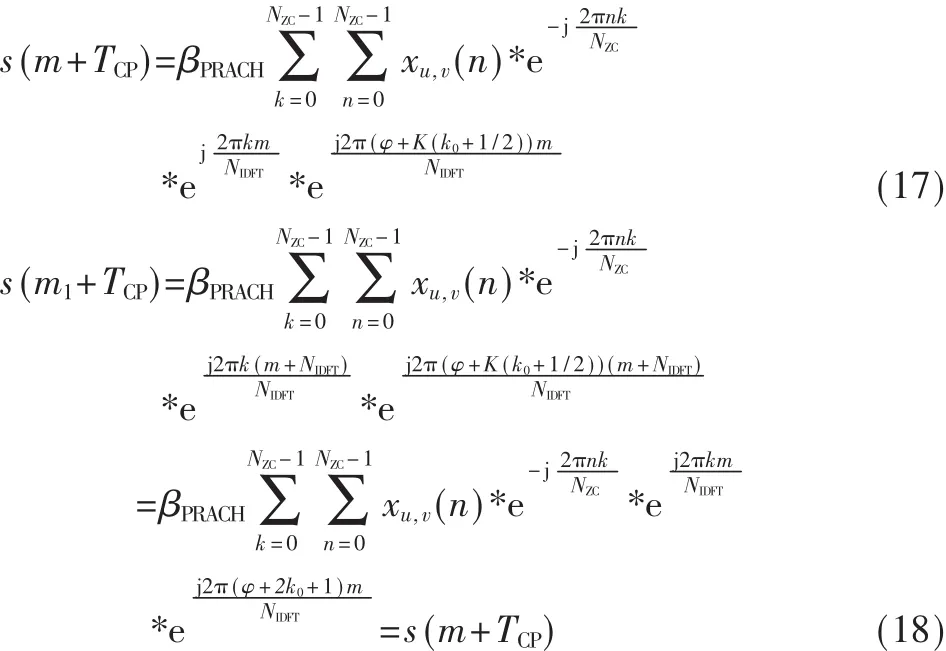

由上述推导可知,CP的插入实际上就是将生成的前导后面的一部分数据搬到前导的最前端,完成CP的插入。
2 PRACH基带信号的实现
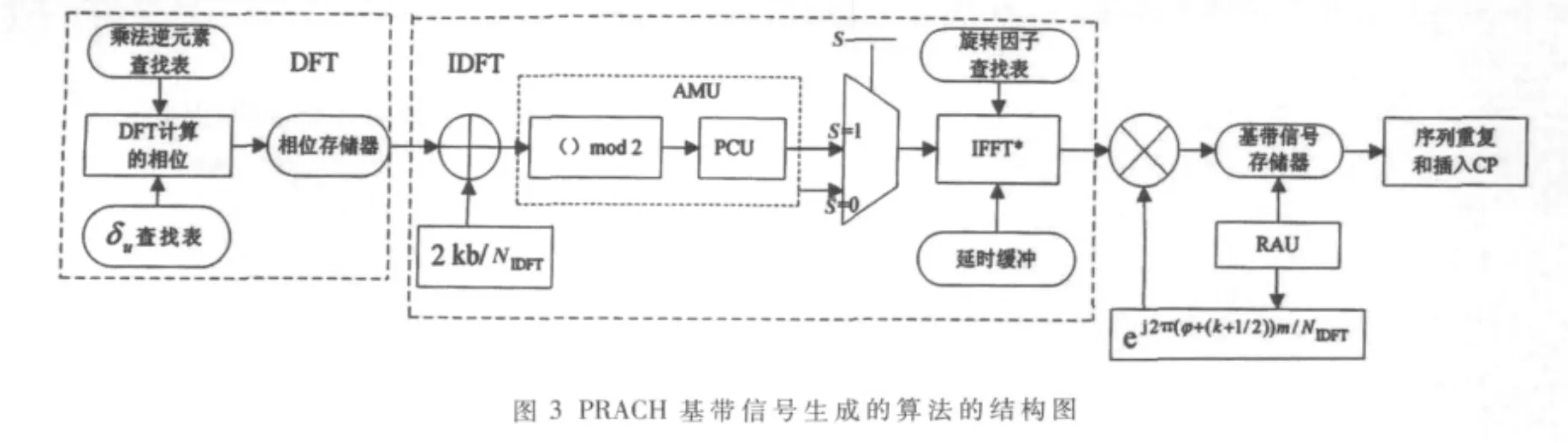
PRACH基带信号实现的结构图如图3所示。
由DFT实现的推导式(14)首先将u-1提前存储在查找表中。为了节约存储空间,把雅各比符号δu代替αu存储在查找表中。根据存储表中的u-1和 δu结合公式,计算 DFT运算的相位Phase of DFT=[(u-1k(k+1)+(1-u-1)k(NZC+1)+αu+2kCv)mod(2NZC)]/NZC,Cv是计算前导时的时域偏移量。把计算出的DFT相位存储在SRAM中,对NZC=839而言,存储空间为13 424 bit,每个相位占16 bit宽度,相比较由I和Q两路构成的复数数据而言,相位计算DFT的存储空间节约将近一半。
IDFT计算时,复数相乘和 DFT添加 0,采用 DFT计算出来的相位加上2kb/NIDFT后再进行相位到复数值的变换 (PCU),在实数相位到复数值的变换时同时乘以DFT的幅度因子。经过实相位到复数值变换单元后的数据通过一个由开关S的输入选择单元,当输入数据为0到NZC-1时,开关S置1,将DFT的数据传递给IFFT模块,当输入的数据为NZC到NIFFT-1时,选择开关S置 0,对 DFT数据进行添加0;进行 IFFT计算。
IFFT的实现可以将输入数据取共轭,再做FFT运算,最后将输出的结果取共轭除以总点数就是IFFT的输出结果。因此可以采用FFT的模块来实现[6-7],如图4。
FFT算法基本可以分为两大类,即按时间抽取法和按频域抽取法[2]。按时间抽取法的输入是倒序的,输出是自然顺序的。本文采用时间抽取法的FFT的算法。用J表示当前倒序的十进制数值,对于N=2M,M位二进制数最高位的十进制权值为N/2,且从左向右二进制位的权值依次为N/4,N/8…2,1。因此最高位加 1相当于十进制运算J+N/2。如果最高位是 0(J<N/2),则直接由J+N/2得到下一个倒序值;如果最高位是 1(J≥N/2),则先将最高位变成 0(J=J-N/2),然后次高位加 1(J+N/4),同样在次高位加1时也要对次高位进行判断。如果次高位也为1,此时也需要将该值减去次高位的权值;如果为0,则将该值加上次高位的权值,再判断下一位,依次类推,直到完成最高位加1,逢2向右进位的运算。形成倒序J后,将FFT模块的输入序列重新进行排列,输入到FFT计算模块。进行FFT计算时,先从输入端的第一级开始,共M逐级进行。第L级有2L-1个旋转因子。每一个旋转因子需要完成2M-L个蝶形运算。计算完成每一级后需要对已有的数据进行更新。图4中的控制模块用于产生所有的控制信息。存储器2和3分别用于n和n+t时对应的数据的输入。存储器1用于中间结果的存储,Butterfly运算模块用于每一级的蝶形运算。旋转因子存储器用于每一级的旋转因子的存储。
完成IDFT的数据进行时域频移,根据前导格式判断计算完成的前导序列是否需要进行重复,再根据式(17)和式(18)将计算的前导序列的CP长度序列复制搬移到前导的前端完成CP的插入,得到PRACH基带信号。
3 性能分析
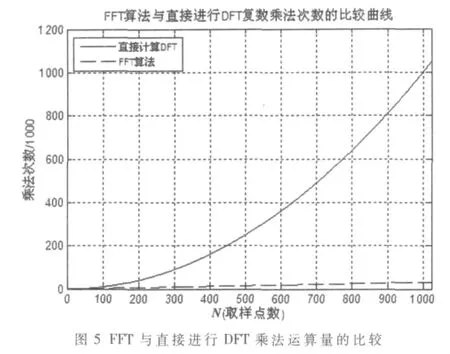
本文从理论分析出发,根据PRACH基带信号的特点,给出了一种PRACH基带信号的生成实现方案。在DFT实现中,改进前的DFT计算的乘法运算次数和加法运算次数比改进的DFT计算的复数的乘法次数和加法运算次数多达703 082次。在IDFT的实现中,采用IFFT计算与直接进行IDFT的乘法次数的比较曲线如图5所示,由图5可以看出,采用IFFT的乘法计算量远小于直接进行IDFT计算,从而减少了PRACH基带信号实现的计算量,提高了整体的性能。能较好地满足LTE系统需要。该方案已应用于TD-LTE射频一致性测试仪表的开发中。
[1]3GPP TS 36.211 v9.0.0 Evolved Universal Terrest-rial Radio Access(E-UTRA)Physical Channels and Modulation(Release 9)[S].2009-12.
[2]丁玉美.数字信号处理[M].西安:西安电子科技大学出版社,2002.
[3]POPOVIC B M.Efficient DFT of zadoff-chu sequences[J].Electronics.letter,2010,46(7):502-503.
[4]BEYME S,LEUNG C.Efficient computation of DFT of zadoff-chu sequences[J].Electronics letter,2010,45(9):461-463.
[5]He Ying,so on.An efficient implementation of PRACH generator in LTE UE transmitters[C].in Wireless Communications and Mobile Compution Conference(IWCMC),2011 7th international,2011:2226-2230.
[6]王林泉,皮亦鸣,陈晓宁,等.基于 FPGA的超高速FFT硬件实现[J].电子科技大学学报,2005,34(2):152-155.
[7]HE S,TORKELSON M.Design and implementation of a 1024-point pipeline FFT processor[C].in Custom Integrated Circuits Conference,1998.Proceedings of the IEEE 1998,may 1998:131-134.
