可重构双基双域模乘器设计与实现
2012-06-03戴紫彬杨同杰
倪 乐,戴紫彬,杨同杰,李 淼,陈 韬
(信息工程大学 电子技术学院,河南 郑州450004)
基于椭圆曲线离散对数问题 (ECDLP)的椭圆曲线密码 ECC(Elliptic Curve Cryptography)[1-2]已经被证明是一种比RSA更安全、计算上更高效的公钥密码体制,因此正逐步取代RSA成为下一代公钥密码标准[3]。作为椭圆曲线密码算法的核心运算,模乘运算的性能至关重要,如何灵活、高效地实现模乘运算是当前的一个研究热点。
ECC的基域有素数域和二进制域两种,在实际应用中,常常需要能够支持两个域上的模乘运算,为此设计了一种双域模乘器是一种有效的解决方案。Montgomery模乘算法[4]是目前应用最为广泛且最为高效的模乘算法,它将传统模乘运算中的除法运算以移位操作代替,大大加快了模乘运算的速度和效率,非常适合硬件实现。由于两个域上的传统模乘器设计的延迟不同,因此本文选取适合双域运算的Montgomery算法进行分析,采用选取不同字长的设计方法,提出了可重构的双基双域模乘器设计方案。结果表明,本设计有效提高了二进制域上模乘运算的速度,使得两个有限域上模乘运算的时钟频率更加匹配。
1 双域Montgomery模乘算法
素数域和二进制域上基于字的Montgomery模乘算法如算法1所示。其中,A、B表示被乘数和乘数,N表示模数,C表示Montgomery模乘运算的乘积。字长为w,基r为 2w,s=「m/w(m是模数N的位长)。A(i)代表A的第i个字,B(j)、C(j)、N(j)分别代表B、C、N的第j个字。
算法1基于字的Montgomery模乘算法
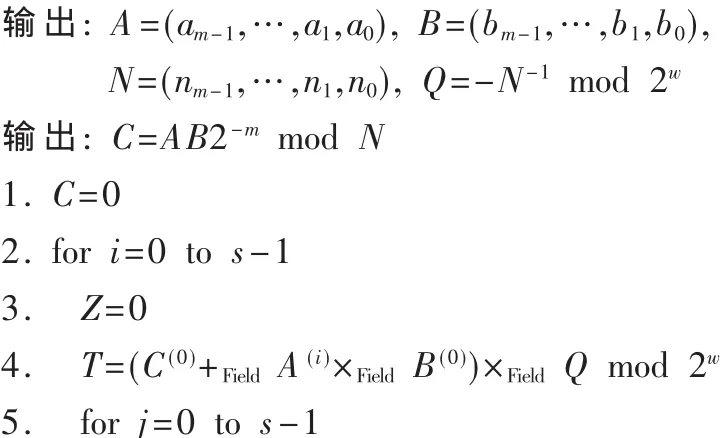
算法1是一种对原始Montgomery模乘算法的改进,它对操作数按字进行了分割,把大整数的乘法运算分割成小整数的乘法,避免了硬件实现中大整数运算带来的时钟延迟较大的问题。算法中运算+Field、-Field和×Field的具体定义是某一个有限域上的运算:对于素数域,为普通整数的加、减法和乘法运算;对于二进制域,元素在运算中都采用多项式表示形式,加、减法运算就是“异或”运算,乘法运算比较特殊,部分积的累加采用对应位“异或”的方式。算法最后(第10步)的比较和减法运算只针对素数域,二进制域不需要这一步。
2 可重构双基双域模乘器设计
2.1 传统双域模乘器分析
传统的双域模乘器大都采用单一基的设计,即素数域和二进制域采用相同的字长进行运算,最有代表性的就是Akashi Satoh设计的双域模乘器[5],其中的逻辑运算单元完成算法1的第2~第9步,是整个电路的关键路径。然而关键路径的延迟又和运算选取的基域密切相关,二进制域上的加法运算是“异或”运算,而素数域上的加法是带进位的普通整数加法运算,缩短延迟最有效的办法是采用进位保留加法器(CSA)。一级CSA的最大延迟为 2TXOR(“异或”门的传输延迟)是“异或”运算的两倍,因此在采用相同运算字长的情况下,这种双域结构的模乘器在时钟频率上必然取决于延迟较大的素数域运算,一定程度上影响了二进制域上模乘运算的速度。
为了解决上述问题,本文采用双基的设计思想,即素数域和二进制域上的运算采用不同的字长,通过增大二进制域上模乘运算单次扫描的字长,达到减少模乘运算消耗的总时钟周期数的目的,解决了由于时钟频率降低所带来的运算时间增大的问题。
2.2 运算字长的选择
算法1中最核心的运算是内循环中第6步的2次乘法和3次加法运算,而乘法运算又是GF(p)和GF(2m)上延迟时间差距最大的运算。因此下面将针对双域模乘器进行分析,通过对两个域上不同字长下模乘器延迟时间的比较,选择出能够使两个域上模乘器延迟时间相当的字长。
根据分析,在字长相同时,素数域上的整数乘法运算延迟要大于二进制域上的乘法运算延迟,因此二进制域上的字长应该大于素数域上的字长,才能使得两个域上模乘器的延迟大体相当。
假设X、Y∈GF(2m),并且X和Y二进制形式表示的字长都是k=2w。
若用一般方法,X和Y相乘先通过k2个“与”门生成k个k-bit位宽的部分积,再通过(「k/27+「k/22+「k/23+…+「k/2「log2k)(k-1)个“异或”门对这些部分积进行求和。
Karatsuba-Ofman算法[6]是一种利用w-bit乘法运算来实现2w-bit乘法运算的方法。X和Y可以表示为:X=2wXH+XL,Y=2wYH+YL, 其中XH和XL分别表示被乘数X的高半部分和低半部分,YH和YL分别表示乘数Y的高半部分和低半部分。
X和Y的乘法表示为:
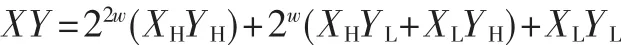
共需要4次乘法和3次加法运算。通过对XHYL+XLYH的进一步简化,X和Y的乘法还可表示为:

简化后需要3次乘法和6次加法运算。这种方法称为一级Karatsuba-Ofman方法。
Karatsuba-Ofman算法不仅可以单独实现模乘器,还可以嵌套完成更大字长的模乘器。一重Karatsuba-Ofman嵌套的设计方法称为二级Karatsuba-Ofman方法。
在0.18 μm CMOS工艺下对上述模乘器设计进行综合,表1比较了整数模乘器与不同方法实现的二进制域模乘器的延迟。从表1发现,16 bit整数模乘器的延迟与64 bit二级Karatsuba-Ofman模乘器的延迟最为接近,符合两个域上模乘运算延迟更加相近的要求。因此,本文选择素数域整数模乘器和二级Karatsuba-Ofman方法实现的二进制域模乘器,运算字长分别为16 bit和64 bit。

表1 两个域上模乘器延迟比较
2.3 可重构模乘器设计
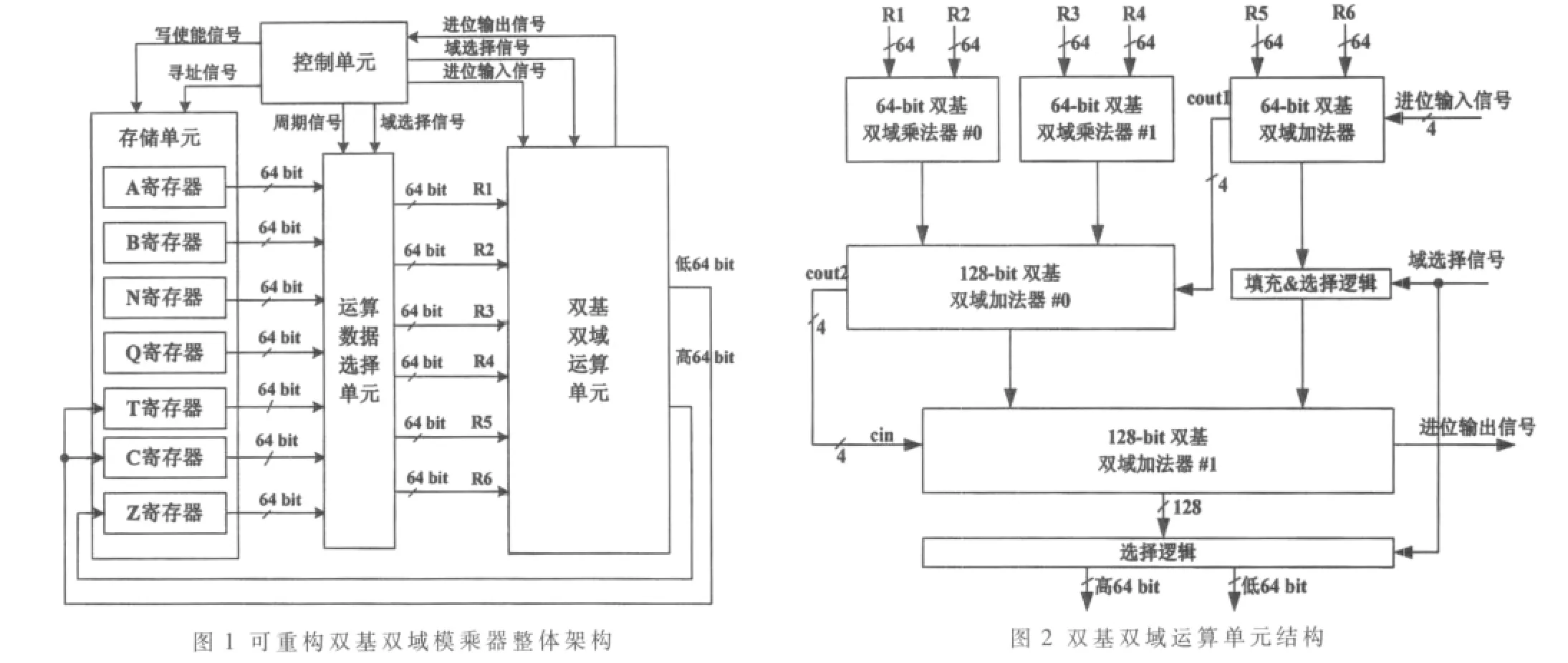
结合上述分析,本文设计的可重构双基双域模乘器整体架构如图1所示,主要由存储单元、双基双域运算单元、控制单元以及运算数据选择单元构成。其中,存储单元用来存储运算参数A、B、N、Q以及中间变量T、C、Z;双基双域运算单元完成算法1的第2~第9步运算,运算数据位宽为64 bit,执行二进制域上的运算时为单路运算,执行素数域上的运算时变为4路并行运算;控制单元为存储单元生成读写控制信号,对运算数据选择单元的输出进行选择,并对双基双域运算单元的进位信号进行寄存。
双基双域运算单元结构如图2所示,主要由2个并行的64 bit双基双域模乘器、1个64 bit双基双域加法器和两个128 bit双基双域加法器组成。该单元能够用一次操作完成算法1中最核心的第6步运算:二进制域运算时,运算字长 64 bit,在一个时钟内单路完成一轮内循环运算;素数域运算时,每路运算字长 16 bit,4路并行完成相邻4个外循环运算。
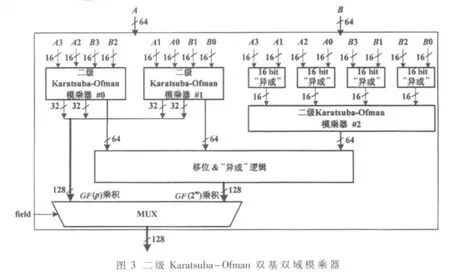
图2中的两个64 bit双基双域模乘器采用二级Karatsuba-Ofman方法实现,电路结构如图3所示,主要包含3个Karatsuba-Ofman模乘器,#0和 #1为16 bit位宽,#2为64-bit位宽。该模乘器完成的功能根据有限域选择信号field的不同分为两种情况:二进制域时,完成64 bit输入数据A和B的乘积A×B;素数域时,输入数据 A和B自高到低分割成 4个16 bit,并行完成 A3×B3、A2×B2、A1×B1、A0×B0 4 路整数乘法运算。
3 功能仿真与性能分析
3.1 功能仿真
本文采用Verilog语言对可重构双基双域模乘器进行RTL级描述,选用Mentor公司的ModelSim 6.1f进行硬件功能仿真,以验证设计的正确性。以下给出了GF(p)上 384 bit和 GF(2m)上 234 bit Montgomery模乘运算的仿真结果(数据按照低32 bit在前,高 32 bit在后的顺序输入和输出)。
素数域上的运算数据:


乘积AB2-384mod N:

二进制域上的运算数据:

乘积A(x)B(x)x-256mod N:
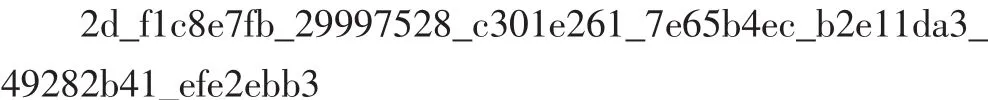

表2 不同长度下模乘运算时钟周期数比较
3.2 性能分析
素数域上模乘运算采用4路并行运算,每一路运算消耗s+1个时钟周期,一共循环「(s+1)/4次。同时相邻两路运算之间相差3个时钟周期,最后一路运算结束需要额外3×「(s+1)%4-1个时钟周期,因此运算时间为:

二进制域上模乘运算采用单路循环完成,每一路运算消耗s+1个时钟周期,一共循环s+1次,因此运算时间为:
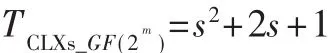
表2列出了本设计与其他设计在GF(p)和GF(2m)上不同长度下模乘运算时钟周期数的比较结果。
从表中可以看出,在GF(p)上,本设计选用的基比参考文献[5]小,所以时钟周期数平均是参考文献[5]的1.5倍;与参考文献[7]相比,虽然选用的基相同并且都是4路并行,但是本文采用二级Karatsuba-Ofman方法实现,使得算法1中的1轮内循环只需要1个时钟周期,比参考文献[7]平均缩短了48%。在GF(2m)上,在选用相同基的情况下,本设计的时钟周期数平均比参考文献 [5]和参考[7]缩短了46%。
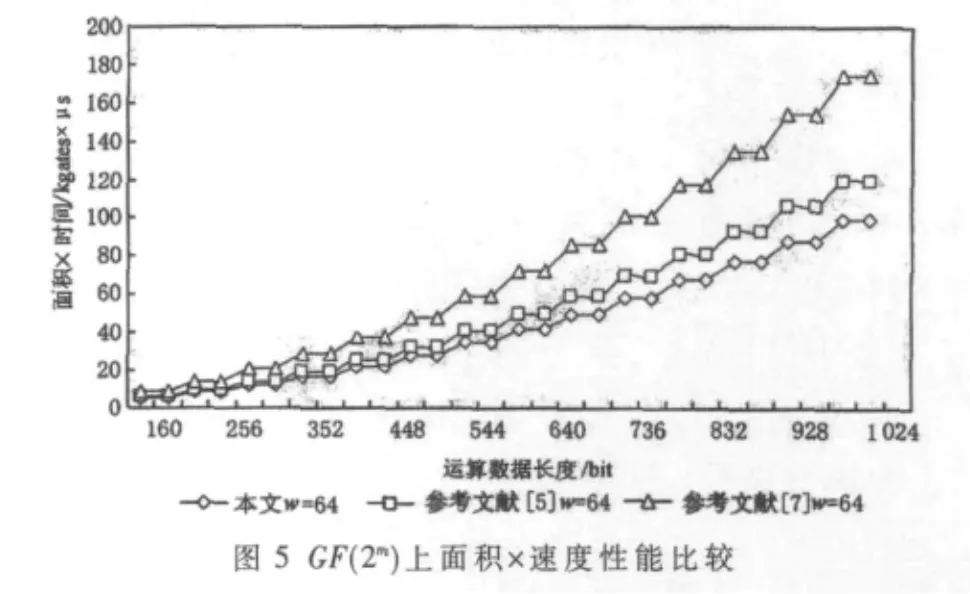
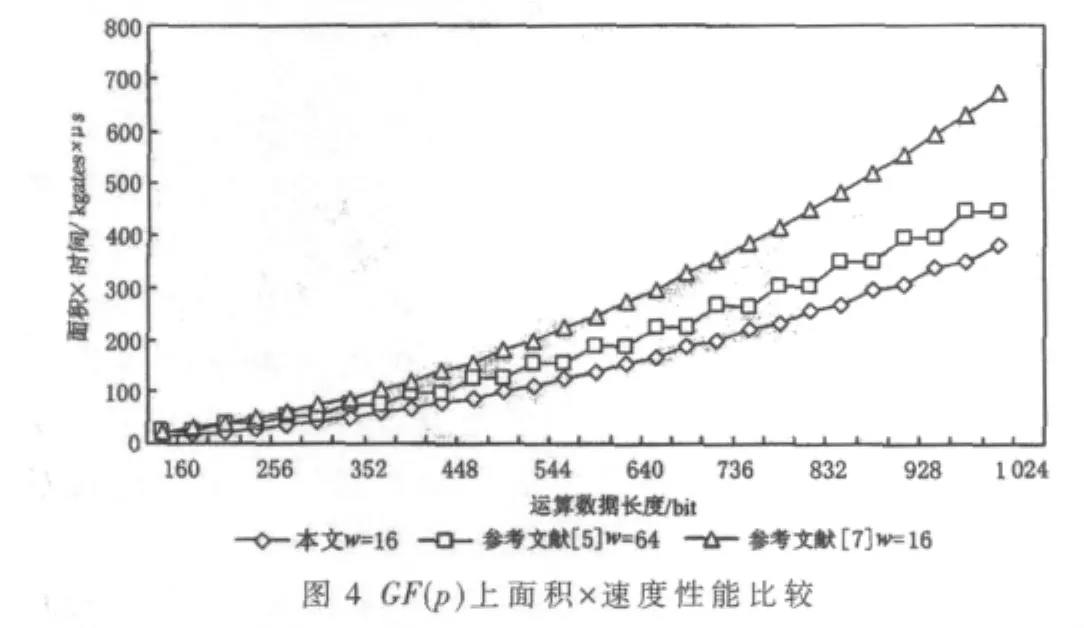
不同类型模乘器的电路面积和运算速度有着较大的差别,而单一地从某一方面进行性能衡量都是不全面的,所以通常以面积与速度的乘积作为比较全面的衡量性能优劣的重要指标。图4、图5分别给出了本文设计的可重构双基双域模乘器与参考文献[5]、[7]设计的模乘器的性能比较。可以看出,无论是在GF(p)还是在GF(2m)上,本文设计的模乘器都具有最小的面积×速度,电路延迟较小,电路规模适中,综合性能更好。
本文基于字级的Montgomery模乘算法,针对双域模乘器设计中存在的二进制域上模乘运算效率不高的问题,设计了一种新的可重构双基双域模乘器。根据以上的分析和比较,本文设计的可重构双基双域模乘器在灵活性、运算速度以及面积等方面具有优势,与双域上采用单一基的模乘器相比,在GF(2m)上的模乘运算效率得到显著提高,满足现代通信网络对公钥密码处理高速性和灵活性的要求。
[1]MILLER V.Use of elliptic curves in cryptography[A].In:H.C.Williams.Advances in Cryptography-CRYPTO′85[C].Heidelberg:Springer-Verlag,1986:417-426.
[2]KOBLITZ N.Elliptic Curve Cryptosystems[J].Mathematics of Computation,1987(48):203-209.
[3]陈华锋.椭圆曲线密码算法及芯片实现方法研究[D].杭州:浙江大学,2008:56-60.
[4]MONTGOMERY P L.Modular multiplication without trial division[J].Mathematics of Computation,1985,44:519-521.
[5]SATOH A,TAKANO K.A scalable dual-field elliptic curve cryptographic processor[J].IEEE Transactions on Computers,2003,4(52):449-460.
[6]Zhou Gang,MICHALIK H,HINSENKAMP L.Complexity analysis and efficient implementations of bits parallel finite field multiplier based on karatsuba-ofman algorithm on FPGAs[J].IEEE Transcations on Very Large Scale Integration(VLSI)Systems,2010,18(7):1057-1066.
[7]TANIMURA K,NARA R,KOHARA S.Scalable unified dual-radix architecture for montgomery multiplication in GF(p)and GF(2n)[C].Design Automation Conference,Seoul,March 2008:697-702.
