弹体落水过程中附加质量变化影响研究

倪宝玉，孙士丽，孙龙泉，张 成

(1.哈尔滨工程大学 船舶工程学院，哈尔滨 150001;2.上海交通大学 船舶海洋与建筑工程学院，上海 200240;3.中国舰船研究设计中心，武汉 430064)

水下航行器出、入水过程涉及到流固耦合问题，自70年代以来，在数值研究流体结构相互作用的方法上取得了很大的进展，并深入到许多复杂的流体结构系统。其研究方法可分为弱耦合法和强耦合法［1］。强耦合方法则是对流体和结构分别建立运动方程，采用数值方法将其耦合求解。弱耦合法即对流体作简化，将流体对结构的作用表达为流体力的形式，如附加质量力等。该方法形式简单，计算量相对较少，在工程中得到广泛的应用［2］。

用附加质量度量流体惯性大小，它是影响水下航行器的水动力特性和动载荷特性的重要参数之一［3－4］，附加质量和阻尼力的计算是直接影响到水下结构运动的关键性问题［5－7］。球体等简单形状物体的附加质量可通过解析解求得，复杂形状物体的附加质量通常通过估算法或Hess－Smith［8］方法求得。水下航行器入水过程中，由于流场的作用引起的附加质量会改变结构的动力学和运动学特性［9］。贾亮等［10］把结构简化为梁单元，主要对附加质量对结构弯矩的影响进行了研究。李明等［9］将航行体简化为梁模型，对出水过程中附加质量的变化航行体横向振动的影响进行了研究。王科等［11］应用边界积分方程的方法研究了FPSO型采油平台的附加质量和阻尼力问题。袁振伟等［12］分析了各种因素对动力附加质量和动力附加阻尼的影响。

飞行器入水过程中附加质量是随入水深度发生变化的，在这个过程中附加质量的改变有多大，附加质量随时间改变的快慢如何，其对结构的运动参数有多大影响，目前相关文献研究较少。为此，本文首先在分析国外文献的基础上，给出含有附加质量变化率的入水砰击力简约表达式。其次，给出考虑附加质量变化的结构运动方程，考虑由于附加质量的变化产生的阻尼系数的改变项。最后以弹体入水为例，分析弹体入水过程中刚体运动、弹性振动引起的附加质量的变化情况，以及相应砰击力的变化。

1 落水砰击力的解析解

为了分析方便，本文首先研究物体以某一定常速度垂直落水情况下，其对应的水动力解析解。如图1所示，定义一个迪卡尔坐标系O-XYZ，原点O位于未扰动的自由液面上，Z轴竖直向上。物体以一竖直速度W(W为负值时表示物体向下运动)运动的情况。假定流体满足不可压缩、无旋、无粘的假设，可应用势流理论进行求解。假设在自由液面SF和无穷远边界S∞速度势φ=0。

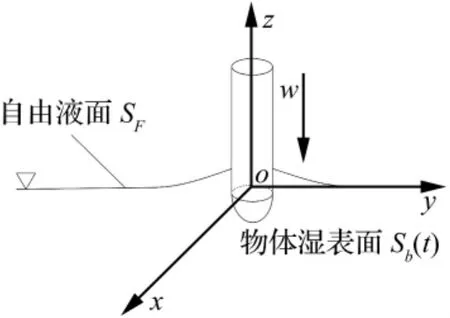
图1 物体垂直入水运动示意图Fig.1 The sketch map of vertical entry in the water of a body

为了能够将物体所受的水动力表达成含有附加质量变化率的形式，本文从能量观点［13－14］获得砰击力。流场中的动能E可写成如下形式:

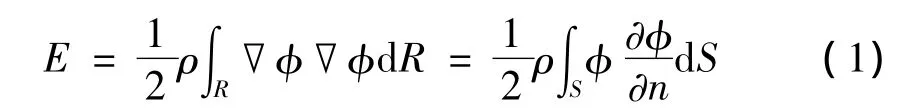
式中:ρ为流体密度，φ为速度势，▽为哈密尔顿算子，R为S包围的整个流域，S为包含物体湿表面Sb(t)、自由面SF和无穷远边界面S∞在内的整个流域的边界面，n为流域边界的法向(指向流域外为正)。考虑到自由面边界和无穷远处边界条件，可得:

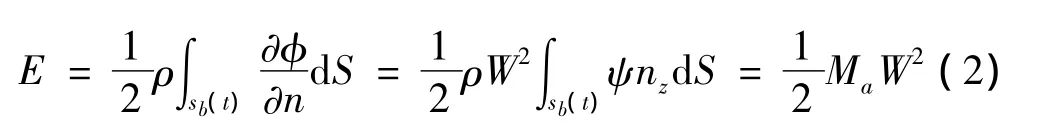
式中:ψ=φ/W为单位速度势，Ma是附加质量，根据定义为:

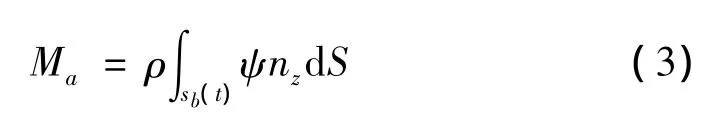
将输运公式应用于式(1)，经过变化［14］:

考虑到物体所受的流体动压力满足:

式中未考虑静水压的影响。将式(5)、式(2)代入式(4)中，即可获得含有附加质量变化率的流体动压力计算表达式为:

由上式可见，在考虑附加质量变化率后，物体所受的流体动压力不仅和加速度d W/d t有关，还和附加质量变化率d Ma/d t有关。有趣的是，方程(6)貌似和著名的动量定律导出的公式)相矛盾。而实际上，对于动量定理中，Fe是刚性物体受到的所有合外力，M是刚体本身的质量。对于式(6)中F仅仅是物体受到的水动力，Ma为物体扰动的流体的质量。换句话说，根据牛顿第三定律来看，流体本身除了受到来自物体的扰动力F，在其他边界(如无穷远边界)还将受到其他的力。关于这点，文献［14］已经有了深入的讨论，并通过数学演绎推导出的式(6)实质上和势流理论中著名的近场公式是一致的。

关于瞬态湿表面积物体附加质量的求解，本文采用时域格林函数法，其对应的具体相关理论见文献［8］，主要的思想是引入时域格林函数求解如下定解条件:

式中:vn为物体运动的法向速度。自由液面的初始条件为:

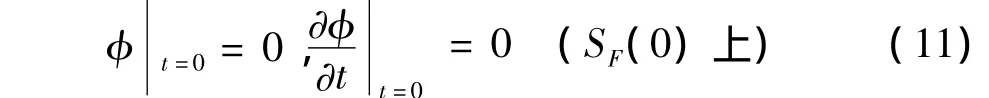
速度势的积分方程可表示为:

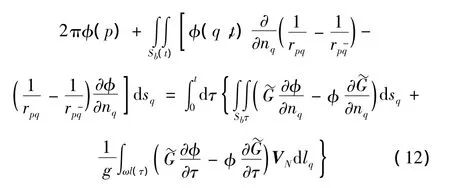
式中:p为固定点，q为动点，?rpq为点p，q的距离为点p，q关于自由面的镜像点的距离，ωl(τ)表示τ时刻弹体瞬时表面与xoy平面的交线，N是平面曲线ωl(τ)的单位法向量，指向弹体内部，VN是周线ωl(τ)沿法向N的法向运动速度为时域格林函数的兴波项。通过边界积分法求得速度势φ后，代入式(3)即对应时刻和对应运动方向的附加质量。边界积分方程的求解方法见文献［8］或文献［15］。

2 考虑附加质量变化率的结构运动方程

本节在式(6)的基础上，将附加质量变化率考虑到结构运动方程中，推导针对弹体模型的砰击力计算公式。首先将式(6)中d Ma/d t项时空分离，改成如下形式:

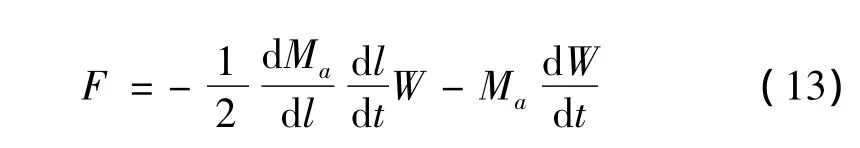
式中:l表示弹体轴向浸湿长度，对于上文考虑的弹体垂直入水，有d l/d t=－W，d Ma/d l表示单位入水长度引起的附加质量的变化。将d Ma/d t时空分离之后的好处在于d l/d t将直接与弹体运动速度有关，而附加质量的空间变化率d Ma/d l则和弹体运动状态(横向刚体运动、轴向刚体运动、弹性振动)有关。

设结构的运动方程可离散成多自由度系统的运动方程式，如下所示:

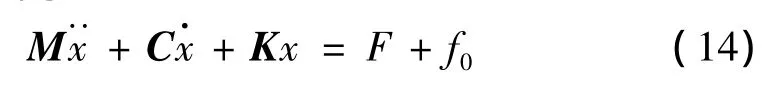
式中:M为结构的质量矩阵;C为结构的内阻尼矩阵;K为结构的刚度矩阵;F为结构运动引起的水动力合力;f0为除此之外的外界激振力。将式(13)代入式(14)得到:

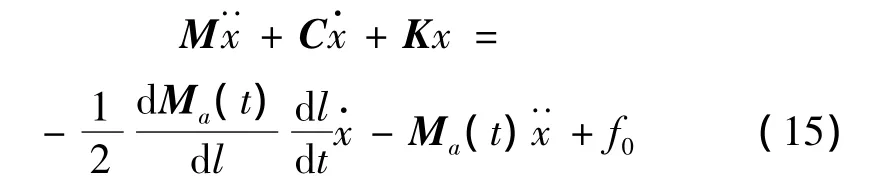
设x=φq，φ为干模态振型，q为弹体真空中的主坐标矢量:

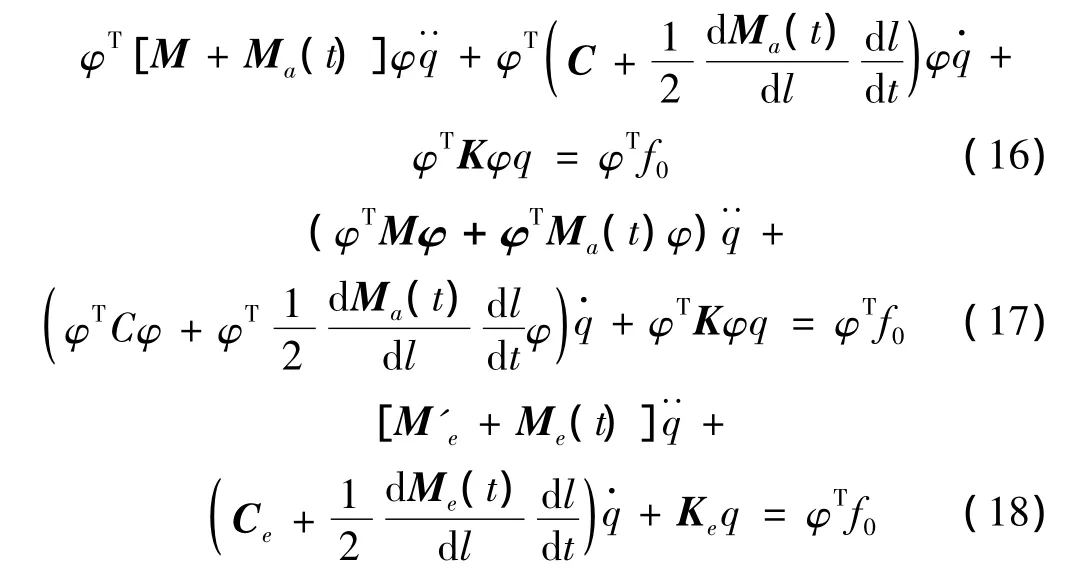
式中:M'e为主质量矩阵，Me(t)为主附加质量矩阵，Ce为主阻尼矩阵，Ke为主刚度矩阵。由上式可见，附加质量不仅会影响质量阵，还会影响结构阻尼阵，对应主阻尼阵增量为所以，弹体在出入水过程中，由于附加质量的影响，其对应的振动频率、阻尼系数等会剧烈变化，对应的结构振动特性较之水中有很大变化。

3 算例分析

3.1 方法验证

本文基于势流理论，采用边界元方法，开发三维计算程序，计算弹体各阶湿模态的附加质量随入水长度变化规律。在探讨规律之前，先通过简单的弹体运动验证本文程序的有效性。取圆柱体水中绕流模型作为刚体附加质量的计算模型，参数见表1。

无限长直圆柱水中绕流模型单位长度附加质量的理论解是πa2，a是圆柱体半径。

从表1可以看出，用数值方法计算附加质量存在一定的误差，并且长度直径比越大，计算所得的附加质量越接近于理论值.这是因为选取的圆柱体模型为有限长，而圆柱体水中绕流模型附加质量理论解是基于无限长直圆柱假设而得到的结论。因此，本文数值解有较高的精度，验证了用数值方法计算刚体附加质量的正确性和有效性。

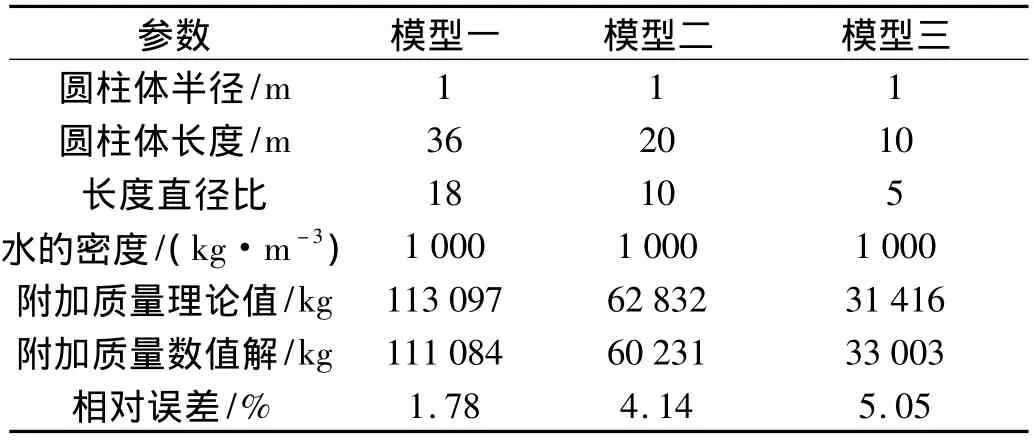
表1 刚体运动附加质量Tab.1 Added mass of the rigid body motion

3.2 弹体斜入水算例

选择某一工况进行物体入水附加质量变化研究。模型入水示意图如图2所示，其中O－XYZ为大地坐标系，o－xyz为弹体随体坐标系。计算工况为:弹体全长L=1.0 m，初始俯仰角 θ=65°，浸湿长度 l选取为物体水下部分在垂向的投影长度，则最大的浸湿长度为0.9 m。初始弹体运动水平速度方向向右，大小为0.6 m/s，垂向速度方向向下，大小为16 m/s。

图2 弹体斜入水运动示意图Fig.2 The sketch map of oblique entry in the water of a body

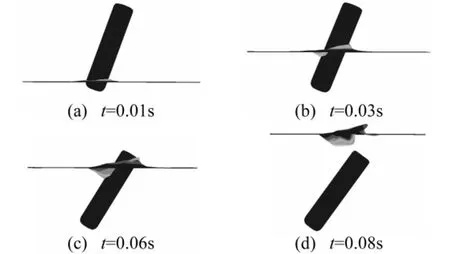
图3 弹体落水过程数值模拟Fig.3 The simulation of a missile entering into water

弹体入水运动的姿态变化示意图如图3所示。

从图3中可见，在t=0.01 s时，弹体头部基本完全入水，流场在物体挤压下开始上涌;0.03 s时弹体左侧流体下陷，右侧流体上涌，这是因为弹体在向下运动的同时，还存在一向右的速度，使弹体挤压其右侧流场，偏离其左侧流场;t=0.06 s时，弹体尾部开始入水，自由液面变形较大;t=0.08 s时，流体完全淹没弹体，自由面产生大变形，此后弹体将在流场中自由运动，液面在较长时间后将趋于平静。本文的数值模拟中没有考虑弹体入水携带的肩空泡问题，故将在一定程度上与真实物理过程有所差异。

本文最主要关心弹体入水过程的中瞬态附加质量Ma以及附加质量变化率d Ma/d l问题。Ma及d Ma/d l本身和结构的落水运动没有关系，仅和湿表面形状以及模型所在水下位置有关。图4～图8中给出图3入水模型相关方向的Ma及d Ma/d l的变化曲线，各图中横坐标Z0为弹体头部顶点在大地坐标系下的垂向坐标。

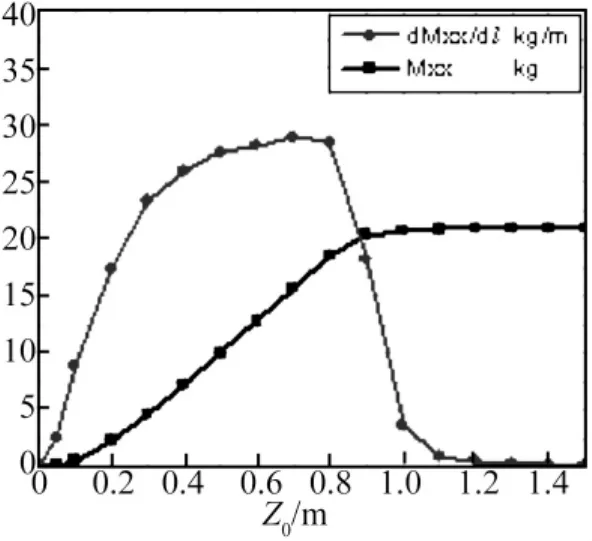
图4 X方向附加质量Mxx及其变化率d Mxx/d lFig.4 The added mass in X direction Mxx and its variation d Mxx/d l

从图4可见，X方向附加质量Mxx随弹体入水深度增大而增大，当Z0超过0.9 m以后，附加质量随浸水长度变化微小。因为Z0小于0.9 m时，湿表面随浸水长度的增加而增加，附加质量也随之增加。Z0超过0.9 m后，弹体完全入水湿表面不再改变，只不过模型所在位置的水深发生变化，附加质量Mxx变化很小。

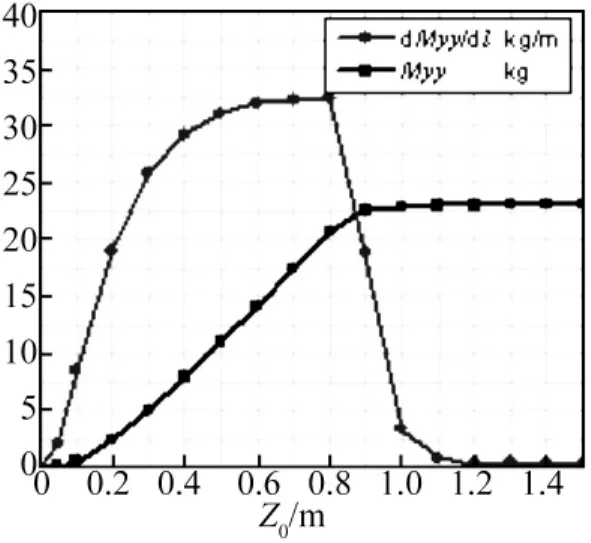
图5 Y方向附加质量Myy及其变化率d Myy/d lFig.5 The added mass in Y direction Myy and its variation d Myy/d l

Z0小于0.9 m时，附加质量变化率d Mxx/d l随浸水长度l的增加而增加。Z0超过0.9 m，附加质量变化率d Mxx/d l随入水长度的增加而迅速减小，并趋于0。这是因为Z0小于0.9 m，主要影响附加质量的是湿表面积，Z0大于0.9 m，主要影响附加质量的是模型所在位置的水深。湿表面对附加质量的影响要比水深影响大得多。

从图5可见，Y方向附加质量 Myy及其变化率d Myy/d l的变化趋势和X方向基本一致，只不过Y方向附加质量比X方向附加质量稍小，X方向附加质量的最大值达到32.6kg，而X方向附加质量的最大值只有28kg左右。这是因为弹体OYZ平面上存在倾角，因此在Y方向的投影面积比在X轴的投影面积小，致使Y方向附加质量比X方向附加质量略小。

图6 Z方向附加质量Mzz及其变化率d Mzz/d lFig.6 The added mass in Z direction Mzz and its variation d Mzz/d l

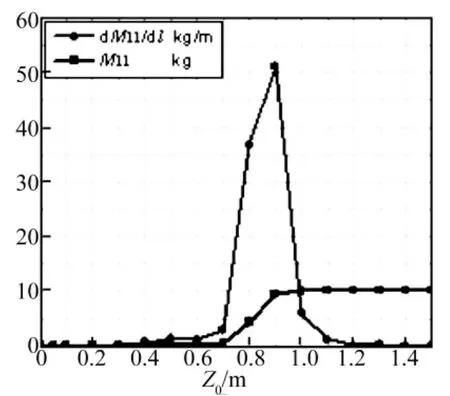
图7 一阶弹性振动附加质量M11及其变化率d M11/d lFig.7 The added mass of the first vibration M11 and its variation d M11/d l

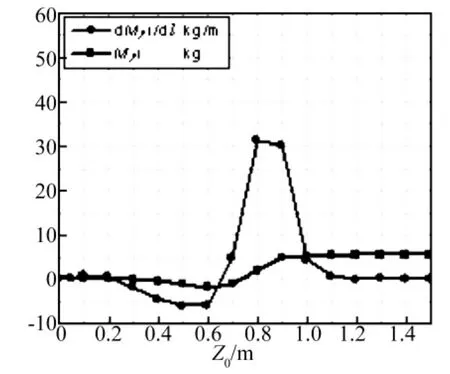
图8 Y方向和一阶弹性振动耦合附加质量My1及其变化率d My1/d lFig.8 The coupling added mass My1 and its variation d My1/d l

从图6可见，轴向附加质量变化率d M/d l存在两个明显的峰值，峰值出现时刻分别对应物体头部和尾部入水。可见湿表面积Z向投影的剧烈变化导致了附加质量变化率的峰值存在。同时这两种峰值在垂向冲击力的变化中也可以观察到。另外，在第一个和第二个峰值之间，附加质量变化率dMzz/dl随浸水长度的变化很小，这与Mxx，Myy的变化趋势是不同的，这主要是因为结构在Z方向投影面积的变化很小，Z0小于0.9 m时，Z方向附加质量Mzz近于线性增加。Z0大于0.9 m后，Z方向附加质量Mzz基本维持某一定值附近。

图7为一阶弹性振动的附加质量及其变化率随入水长度的变化曲线。从中可见，在物体尾部浸入水中时变化特别大。这是由结构本身的一阶振型决定的。本文研究的结构对应的一阶振动在尾部振动最为剧烈，其它部分振动很小。致使在弹体尾部浸入水中时，附加质量变化特别大。Z0大于0.9 m后，一阶弹性振动附加质量M11随入水长度的变化同样不明显。

图8为弹体一阶弹性振动与Y方向刚体运动的耦合附加质量变化趋势。对于本文研究的弹体结构，其一阶弹性振动方向主要是沿Y方向，在X方向振动量很小，故其与X方向刚体运动耦合附加质量非常小，此处不再给出。从图8中可见，一阶弹性振动与Y方向耦合附加质量却非常大。因此，弹体在做刚体运动的同时伴随弹性振动，耦合附加质量是不可忽略的。同时，耦合附加质量呈现波动的趋势，这和振型密切相关的。

3.3 弹体直入水算例

在研究了刚体运动、弹性振动诱发的附加质量随浸湿长度变化的趋势后，本文接着研究弹体落水过程中垂向砰击力的变化趋势。选取的计算工况示意图如图1所示，其中弹体长1.0 m，边界元模型与3.2节一致。垂直入水速度为10 m/s，与3.2节算例中自由落水有所不同的是，本节中强制弹体落水速度保持10 m/s匀速不变，对应的弹体姿态也保持垂直不变。

这里采用两种数值方法计算弹体遭受的砰击力，一是通过公式(5)求解物面上每点压力，然后直接积分求得合力(称为“数值解”);二是应用公式(6)，即先求得附加质量以及变化率，然后直接获得合力。由于附加质量需要数值计算获得，而一旦得到附加质量变化率，则可应用式(6)计算合力，故本文称此方法为“半数值半解析解”。

图9 “数值解”与“半数值半解析解”对比Fig.9 The compare between the numerical results and the semi-analytical ones

图9中F3为计算得到的垂向力。从图中可见无论是直接积分法还是通过附加质量变化求得的砰击力均存在两个峰值，第一个峰值是弹体头部触水时，第二个峰值是整个弹体完全浸没水中时。对比图9和图6可发现，垂向砰击力的两个峰值与轴向附加质量变化率峰值出现的时刻相同，所以弹体在头部、尾部入水瞬间对应的砰击力主要来源于附加质量变化率一项，即源于湿表面积的剧烈变化。此外，在误差允许范围内，公式(7)计算得到的力与公式(5)计算得到的力十分接近，再次表明应用附加质量及其变化率计算砰击力的可行性。

4 结论

基于势流理论，本文对弹体落水问题进行研究，基于能量法求得入水砰击力与附加质量及变化率的简约关系。并在此关系基础上研究了附加质量变化对弹体结构振动的影响，以及入水过程中刚体运动、弹性振动引起附加质量的变化。结论如下:

(1)弹体入水过程中垂向砰击力存在两个峰值，分别对应弹体头、尾部接触水面时刻，该砰击力主要源于这两个时刻湿表面积的剧烈变化;

(2)弹体入水过程中附加质量的变化主要取决于弹体形状和湿表面积的变化，水深对其影响相对较小;

(3)附加质量的变化不仅影响结构系统振动的质量阵，还对阻尼系数阵产生的影响。即附加质量不仅改变弹体振动频率，也改变阻尼系数。

［1］蒋 莉，沈孟育.求解流体与结构相互作用问题的ALE有限体积方法［J］.水动力学研究与进展，2000，15(2):148－155.JIANG Li，SHEN Meng-yu.ALE finite volume computations of fluid-structure interaction problems［J］.Journal of Hydrodynamics，2000，15(2):148 －155.

［2］王基盛，杨庆山.流体环境中结构附加质量的计算［J］.北方交通大学学报，2003，27(1):40 －43.WANG Ji-sheng，YANG Qing-shan.Calculation on added mass of structures in fluid environments［J］.Journal of Northern Jiaotong University，2003，27(1):40 －43.

［3］弓三伟，陆宏志，邹正平，等.弹性体和带空泡体的附加质量动态数值计算［J］.计算机仿真，2010，27(4):348－354.GONG San-wei， LU Hong-zhi， ZOU Zheng-ping， et al.Hydrodynamic numerical computation of the added mass of elastic body ＆ cavitation bubble［J］.Computer Simulation，2010，27(4):348 －354.

［4］Newman J N，Sclavounos P D.The computation of wave loads on large offshore structures［C］. Trondheim:Tapir Publishers，1998，2:605 －622.

［5］Buchner B，Vogt A.The effect of bow flare angle on FPSO green water loading［C］.Proceedings of 19th OMAE.New Orleans，2000:1 －8.

［6］Kashiwagi M，Endo K.Yamaguchi H.Wave drift forces and moments on two ships arranged side by side in waves［J］.Ocean Engineering，2005，32:529－555.

［7］Kenneth K C.Underwater shock analysis of a missile launch tube［R］.Research and Technology Department，Naval Surface Weapons Center，1982 －05 －20.

［8］戴遗山，段文洋.船舶在波浪中运动的势流理论［M］.北京:国防工业出版社，2008.

［9］李 明，尹云玉.水下航行体动态响应计算的附加质量探讨［J］.导弹与航天运载技术，2008，4:16－18.LI Ming，YIN Yun-yu.Effect of the added mass on transverse response calculation of submarine vehicle in exiting-water process［J］.Missiles and Space Vehicles，2008，4:16 －18.

［10］贾 亮，荣克林.附加质量对结构出水载荷的影响［C］.全国结构动力学学术研讨会论文集，2007:37－144.

［11］王 科，张 犀，张志强，等.FPSO型采油平台附加质量与阻尼力的分析研究［J］.船舶力学，2011，15(2):40－47.WANG Ke，ZHANG Xi，ZHANG Zhi-qing，et al.Numerical analysis of added mass and damping of FPSO type platform，Journal of Ship Mechanics，2011，15(2):40 －47.

［12］袁振伟，褚福磊，王三保.横向振动圆柱体在流体中的动力学特性［J］.工程力学，2006，23(8):49－52.YUAN Zhen-wei，CHU Fu-lei，WANG San-bao.Dynamic characteristics of a lateral vibrating cylinder immersed in unbounded fluids［J］.Engineering Mechanics，2006，23(8):49－52.

［13］Molin B，Cointe R，Fontaine E.On energy arguments applied to the slamming force［C］.11st International Workshop on Water Waves and Floating Bodies，Hamburg，1996.

［14］Wu G X.Hydrodynamic force on a rigid body during impact with liquid［J］.Journal of Fluids and Structures.1998，12(5):549－559.

［15］张阿漫，姚熊亮.近自由面水下爆炸气泡的运动规律研究［J］.物理学报，2008，57(1):339－353.ZHANG A-man， YAO Xiong-liang. The law of the underwater explosion bubble motion near free surface［J］.Acta Physica Sinica，2008，57(1):339－353.