工程常用湍流模式简介

李园园

（华北电力大学 数理学院，北京 102206）

物理与工程技术研究

工程常用湍流模式简介

李园园

（华北电力大学 数理学院，北京 102206）

总结了以往工程中常用的一些典型的湍流模式，分析了这些模式各自的优缺点及适用范围，其中迟豫模型是一种具有一定普适性的新的湍流迁移模型。

湍流模式；雷诺方程；简介

湍流的研究可以追溯到O. Reynolds提出湍流统计平均方法，至今已有一个多世纪了。在这期间，科学家们一直没有间断过对湍流在理论与实验上的探索，使得人类从对其现象的简单认识，过渡到对湍流本质的深入认识。但由于其存在有结构的多尺度不规则的非常复杂的运动，并且它普遍存在于自然界和工程应用中，因而成为当今一个具有迫切性的科学难题。

求解Navier-Stokes方程是解决湍流问题的关键，因为它描述了湍流的基本物理性质。如果直接求解这个方程，对于工程中复杂的湍流问题，需要的计算量很大，计算机还没有足够的容量和速度来完成这样的计算。因此在解决高雷诺数的实际工程湍流问题时，一般以Reynolds平均运动方程与脉动运动方程为理论基础，并借助经验引入实用的湍流模型假设，从而得出一组描写湍流平均量的封闭方程，这种理论方法被称作湍流模式。

现存的湍流模式基本上还不具备普适性，不能够描述各种复杂湍流运动。但是对某一具体的工程湍流问题，若选择合适的湍流模式，也能得到具有准确性与可靠性的结果。现存的湍流模式有涡黏性模式，其中包括零方程模式，半方程模式，双方程模式；还有二阶矩封闭模式，其中包括雷诺微分应力模式和代数应力模式。一种经过大量实验认证的新的湍流迁移模式——迟豫模型将Tτ和qT归结到一组封闭的迟豫方程组中[1,p2]，因而具有一定的普适性。

1 湍流涡粘模式

1.1 零方程模式

B-L代数涡粘模式[2]是工程上广泛应用的零方程模式。B-L模式多用于湍流边界层，并有内外之分。零方程模式中，除了B-L模式，还有其改进模式[3]，Cebeci-Smith[4]，Johnson-King[5]和Wilcox[6]等提出的模式。这类模式常用于具有中等程度的压力梯度的二维带可压缩流以及存在轻微横向流的三维边界层[7]。

1.2 一方程模式

通过补充湍流动能方程，封闭了湍流动量方程和连续方程的方法为一方程模式，其中的涡粘性与湍能被Kolmogorov及Prandtl提出的关系式联系了起来，而湍能则通过模化后的湍流动能方程来确定，如式(1)所示。

其中C0=0.15，Prt=1。Bradshaw等在二维边界层计算中提出了一种直接将雷诺应力与湍能联系起来的一方程模式[8]，而放弃了涡粘性假设。20世纪初，B-B，S-A模式曾被广泛采用[9]。一方程模式由于简单和省时，所以在工程中仍常被采用。

1.3 双方程模式

典型的双方程模式——k-ε模式将涡粘系数和湍动能及湍动能耗散联系在一起，涡粘系数可写成式(2)：

在k-ε模式中，k和ε则分别由它们的输运方程给出。

在此标准的k-ε模式基础上又发展了非线性k-ε模式[10]。其中有Spezialer的非线性k-ε模式[11]以及重整化群k-ε模式[12]。非线性k-ε模式是各向异性模型，以方管湍流为算例，它能够预测到方管湍流中的平均二次流。在工程中，双方程模式由于计算经济性及一定的精度，被广泛应用。

2 二阶矩封闭模式

2.1 雷诺微分应力模式

在雷诺微分应力模式中，Launder，Reece和Rodi[13]提出用式(3)作为再分配项

此模式包含流线曲率、旋转系统等雷诺应力发展过程，因此它对复杂湍流有较好的预测性。

2.2 代数应力模式

为了二阶矩模式需要的计算机内存和计算时间。Rodi[14]提出一个简化的雷诺应力模式，即代数应力模式。因此在准平衡的三维定常湍流的预测方面，代数应力模式比k-ε好。

3 湍流迁移模型

勃波夫教授和瓦卢耶娃教授为了准确地考虑不稳定性对湍流迁移的影响，必须建立一个新的湍流迁移模型，这种模型把不稳定对湍流迁移的影响考虑为对湍动应力Tτ，湍动热流密度Tq，以及湍动粘滞系数τε的迟豫方程组，并把它称为迟豫模型。

在波动的情况下，计算湍动应力Tτ、湍动热流密度Tq和湍动粘滞系数τε的迟豫方程采用下列形式[1,p2]：

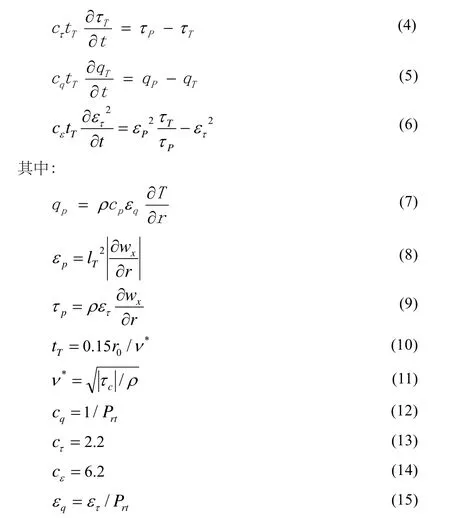
qp、εp和τp分别为各自相应的等价量，tT为湍流的特征时间尺度，cε、cq、cτ和εq为迟豫系数，湍动普朗特数Prt取0.9。

Tτ、Tq和τε的变化要迟缓于各自的瞬时值。他们利用此模型描述了单调变化或周期变化的流量随时间变化的情形，并计算出温度、对流换热系数、速度及阻力系数的分布情况，所有计算结果很好地吻合了现有的实验数据。随后，陈雷[1,p3]用此模型分别对水和空气在加速流与减速流时的对流换热进行了数值模拟，也较好地与实验结果吻合。因此可以认为这种模型具有一定的普适性，有可能成为以后湍流模式发展的主流。

4 结束语

湍流模式在工程中发挥着重要的作用，每一种模式都不能适用于所有的湍流运动。对此问题，国际上也曾试图通过直接数值模拟来解决所有湍流的问题，但最终受限于计算机的容量与速度。即使在未来实现了直接数值模拟，工程师们仍然需要快速精确解决问题的湍流模式。

因此现有的湍流模式发展和完善方向应该是推进和实现它的普适性。针对这一点，也曾有过几种实现的思想。例如有一种是高层次的封闭模式，而实践结果却是产生更多不确定因素，因此适应性未必更广。还有一种是改进含有较多湍流脉动结构信息的统计模式[15]，扩大其适应面。迟豫模型被证实具有一定的普适性。

[1]陈雷.利用湍流迁移模型对变物性流体在非定常流时对流换热实验结果的研究.中国工程热物理学会学术会议论文[A].

[2]Baldwin B S, Lomax H. Thin layer approximation and algebraic model for separated turbulent flows[A]. American Institute of Aeronautics and Astronautics Meeting Papers[C]. 1978: 78-257.

[3]Baldwin B S, Barth T J. A one equation turbulence transport model for high Reynolds number wall bounded flows[A]. The American Institute of Aeronautics and Astronautics Meeting Papers[C]. 1991: 91-0610.

[4]Cebeci T, Smith A M O. Analysis of turbulent boundary layers[M]. McGraw-Hill, 1974.

[5]Johnson D A, King L S. A mathematically simple turbulence closure model for attached and separated turbulent boundary layers[J]. The American Institute of Aero-nautics and Astronautics Journal, 1985, 23: 1684-1692.

[6]Wilcox D C. Reassessment of the scale-determining equation for advanced turbulence models[J]. The American Institute of Aeronautics and Astronautics Journal. 1988, 26: 1299-1310.

[7]Lakshminarayana B. An assessment of computational fluid dynamic techniques in the analysis and design of turbomachinery- the 1990 freeman scholar lecture[J].

-60-Journal of Fluids Engineering, 1991, 113: 315-352.

[8]Bradshaw P, Ferriss D H, Atwell N P. Calculation of boundary layer development using the turbulent energy equation[J]. Journal of Fluid Mechanics, 1967, 28(3): 593-616.

[9]Baldwin B S, Barth T J. A one-equation turbulence model for high Reynolds number wall bounded flows[A]. National Aeronautics and Space Administration Technical Memorandum -102847[C]. 1990: 1-30.

[10]Speziale C G, Ngo T. Numerical solution of turbulent flow past a backwards-facing step using a nonlinear k-ε model[J]. International Journal of Engineering Science, 1988, 26: 1099.

[11]Speziale C G. Analytical methods for the development of Reynolds-stress closures in turbulence[J]. Annual Review of Fluid Mechanics, 1991, 23: 107-157.

[12]Yakhot V, Orszag S A. Renormalization group analysis of turbulence. I. Basic theory[J]. Journal of Science Computation, 1986, 1(1): 3-51.

[13]Launder B E, Reece G J, Rodi W. Progress in the development of a Reynolds-stress turbulence closure[J]. Journal of Fluid Mechanics, 1975, 68: 537-566.

[14]Rodi W. A new algebraic relation for calculating Reynolds stresses[J]. Journal of Applied Mathematics and Mechanics, 1976, 56: T219-T221.

[15]张兆顺,崔桂香,许春晓.湍流理论与模拟[M].北京:清华大学出版社,2005.

（责任编辑、校对：孙海祥）

Brief Introduction of Turbulent Models Commonly Used in Engineering

LI Yuan-yuan
(School of Mathematics and Physics, North China Electric Power University, Beijing 102206, China)

Typical turbulent models usually used in the engineering are summarized. The advantages and disadvantages and applicable scope of these models have been analyzed. Among them tardy model is a new turbulent migration model with a certain universal.

turbulent model; Reynold equation; brief introduction

O357.5

A

1009-9115(2012)05-0058-03

2012-06-20

李园园（1988-），女，陕西富平人，硕士研究生，研究方向为流体力学及传热。