复变函数论中刘维尔定理的应用与推广

张 庆

（唐山师范学院 数学与信息科学系，河北 唐山 063000）

复变函数论中刘维尔定理的应用与推广

张 庆

（唐山师范学院 数学与信息科学系，河北 唐山 063000）

首先给出了刘维尔定理的一种新的证明方法，描述了刘维尔定理的几何意义；其次给出了刘维尔定理在三个方面的应用；最后给出了刘维尔定理在两个方面的推广。

刘维尔定理；整函数；扩充复平面

刘维尔（Liouville J，1809-1882）定理是复变函数论中的一个著名定理，在复变函数论中有着广泛的应用。本文首先给出了刘维尔定理的一种新的证明方法，其次给出了刘维尔定理在三个方面的应用，最后给出了刘维尔定理在两个方面的推广。

1 刘维尔定理及证明

刘维尔定理 有界整函数f(z)必为常数。

注：整函数就是在整个复平面C上解析的函数。

证法1[1]利用柯西不等式证明，见参考文献[1,p127]。

值得注意的是：

（1）刘维尔定理的相应结论在实数域范围内并不成立，例如，函数y=sinx在实数集R内可导且有界，但y=sinx 在实数集R内并不是常数。

（2）刘维尔定理的逆成立，即常数是有界整函数。

（3）刘维尔定理的逆否命题：非常数整函数必无界。

此外由刘维尔定理容易得到推论1。

推论1 若f(z)为有界整函数，则

2 刘维尔定理的几何意义

刘维尔定理具有鲜明的几何意义，其几何意义具体可以叙述如下：

非常数整函数f(z)的值既不能全含于某一圆内，也不能全含于某一圆外。

证明 先证非常数整函数的值不能全含于某一圆内。

于是由刘维尔定理知1/f(z)是常数，从而f(z)必为常数。这与已知矛盾。综上非常数整函数f(z)的值既不能全含于某一圆内，也不能全含于某一圆外。

3 刘维尔定理的应用

3.1 证明代数学基本定理[2]

代数学基本定理：n次多项式

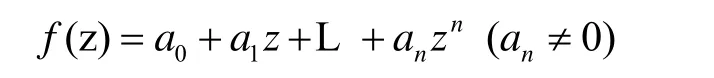
在复数集C内至少有一个零点。

该定理是代数学的基石，但若从代数学知识体系出发，用纯粹的代数方法证明却十分困难且繁杂，因此在高等代数教材中一般未给出它的证明，利用刘维尔定理可以给出该定理一种简洁、完美的证明方法。这是复变函数论在高等代数理论上应用的典范。这一证明方法的主要思路是，将n次多项式

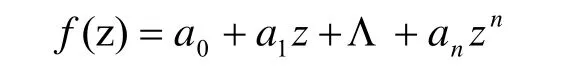
作为一非常数整函数，然后采用反证法得到证明。具体证明见参考文献[2]。

3.2 证明整函数为常数

例1 设f(z)=u(x, y)+iv(x, y)（简记f=u+iv）为一整函数，且存在实数M，使v＞M，∀z∈C，则f(z)为常数。

证明 因为f(z)为整函数，所以

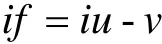
也为整函数。令

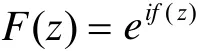
则显然F(z)也为整函数，又于是由刘维尔定理知F(z)为常数，从而f(z)为常数。

3.3 证明复平面C上的最大模原理

复平面C上的最大模原理

若f(z)为整函数，且在C内点z0处取得最大模，则f(z)在C内为常数。

最大模原理是在一般区域D内给出的，证明过程中用到唯一性定理、平均值定理等多个复变函数论中的重要定理，其证明较为复杂难懂，具体证明见参考文献[1,p176]。

当一般区域D改为复平面C时，仅用刘维尔定理即可非常方便的得到复平面C上的最大模原理的证明。

证明 由已知

又因为f(z)为整函数，故由刘维尔定理可知f(z)在C内为常数。

4 刘维尔定理的推广

刘维尔定理可以在扩充复平面上推广，也可以在形式上推广，有以下两个结论。

定理1 扩充复平面上的解析函数f(z)必为常数。

证明 因为f(z)为扩充复平面上的解析函数，所以z=∞为f(z)的可去奇点，因此，

其中b为常数。故存在正数M，R1，使得当

时，有

故由刘维尔定理可知f(z)在扩充复平面必为常数。

则f(z)是一个至多n次多项式或常数。

当n=0时就是通常的刘维尔定理。

证明 因为f(z)为整函数，故可设

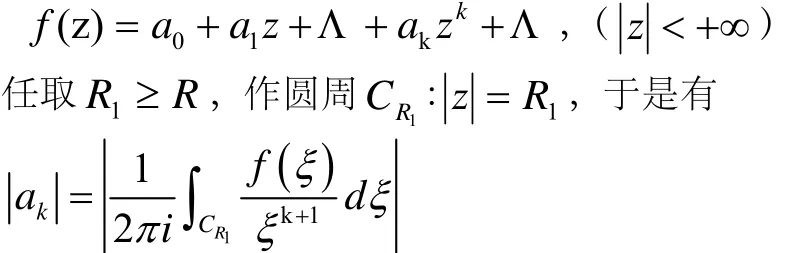
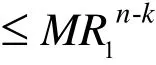
当k＞n时，令R1→+∞，就有

即

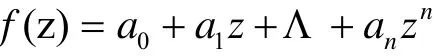
当

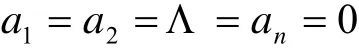
时，f(z)=a0为常数。

综上，f(z)是一个至多n次多项式或常数。

作为推广的刘维尔定理，定理2可以判断整函数的表示形式，具体应用见例2。

例2 设f(z)为整函数，且

则f(z)必为一个n次多项式。

证明 因为

所以∃R＞0及M＞0，当z≥R时，有

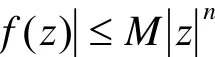
由定理2，f(z)是一个至多n次多项式或常数。若f(z)为常数，则

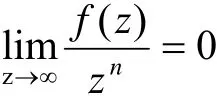
这与已知矛盾。若f(z)为k次多项式（0＜k＜n ）同样有

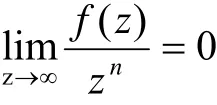
故f(z)只能是n次多项式，由代数学基本定理知f(z)在C内有n个零点。

[1]钟玉泉.复变函数论(第三版)[M].北京:高等教育出版社,2003.

[2]余家荣.复变函数[M].北京:人民教育出版社,1980:99.

[3]钟玉泉.复变函数学习指导书[M].北京:高等教育出版社,1996:222-223.

（责任编辑、校对：赵光峰）

The Application and Generalization of Liouville Theorem in Complex Function Theory

ZHANG Qing
(Department of Mathematics and Information Science, Tangshan Teachers College, Tangshan 063000, China)

This paper gives a new proof of the Liouville theorem. It describes the geometric meaning of the Liouville theorem, then gives the application of Liouville theorem in three areas and generalizes the Liouville theorem in two aspects.

Liouville theorem; integral function; etended complex plane

O174

A

1009-9115(2012)05-0038-03

2012年唐山师范学院教改科研立项（2012001004）

2012-07-20

张庆（1960-），男，天津人，教授，研究方向为函数论。