含参量广义积分分析性质的证明
2012-06-01刘庆辉宋泽成
刘庆辉,宋泽成
(唐山师范学院 数学与信息科学系,河北 唐山 063000)
含参量广义积分分析性质的证明
刘庆辉,宋泽成
(唐山师范学院 数学与信息科学系,河北 唐山 063000)
通过2个引理给出了含参量广义积分分析性质的另外一种证明方法,即直接计算法,这有助于深刻理解含参量广义积分的分析性质。
含参量广义积分;分析性质
引理1 设f(x,y )在x→+∞时关于y在I上一致收
敛于φ(y),且∀x∈[a,+∞),f(x,y )关于y在I上连续,
则∀y∈y0,有
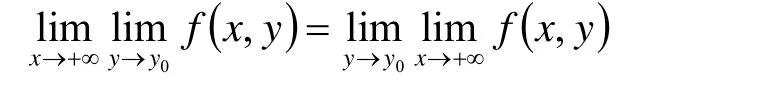
证明 由已知可得:
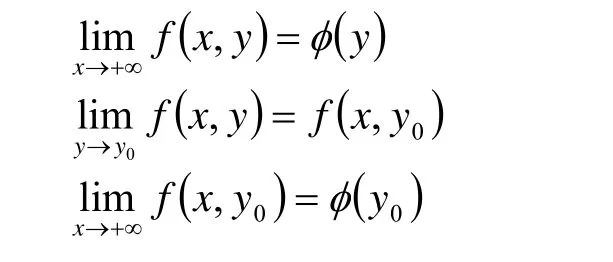
则只需证明
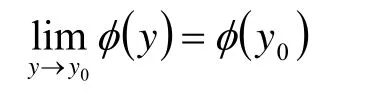
即可。
由于
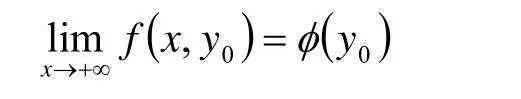
则


定理1(连续性) 若f(x ,y)在I×[c,+∞)上连续,且


定理2(可微性) 若f(x ,y )和fx(x ,y)在I×[c,+∞)上连续,且





[1]华东师范大学数学系.数学分析(第4版,下册)[M].北京:高等教育出版社,2010.
[2]裴礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社,2002.
[3]刘立山,孙钦福.数学分析中的基本理论与典型方法[M].北京:中国科学技术出版社,2005.
(责任编辑、校对:赵光峰)
A Proof of Analysis Properties of the Generalized Integral with Parameter
LIU Qing-hui, SONG Ze-cheng
(Department of Mathematics and Information Science, Tangshan Teachers College, Tangshan 063000, China)
The paper gives another proving method of Analysis properties of the generalized integral with parameter through 2 lemmas: direct method, enriching the content of teaching material, and offering help for our deep understanding of analysis properties of the generalized integral with parameter.
generalized integral with parameter; analysis properties
O174.5
A
1009-9115(2012)05-0034-04
唐山师范学院教育教学改革研究项目(2011001013)
2012-06-05
刘庆辉(1981-),男,河北邢台人,硕士,讲师,研究生,研究方向为函数论。
