基于EPEA的SINS大失准角非线性初始对准方法

赵 红 宇， 王 哲 龙， 姜 鸣， 宫 少 奇， 尚 红

（1.大连理工大学 控制科学与工程学院，辽宁 大连 116024；2.中国科学院沈阳自动化研究所 机器人学国家重点实验室，辽宁 沈阳 100080；3.浙江中控技术股份有限公司，浙江 杭州 310052；4.中国地震应急搜救中心，北京 100049）

0 引 言

实际应用时，捷联惯导系统（SINS）由于受工作环境和陀螺仪精度的影响，地球自转角速率甚至会被陀螺噪声淹没.粗对准结束后[1]，可能出现大方位失准角或大失准角的情况，此时采用小失准角误差模型和线性Kalman滤波技术不能准确地描述系统误差的传播特性[2].因此，研究大失准角下的初始对准技术对于SINS具有十分重要的意义.通常，当粗对准精度无法满足小失准角假设、不进行或不便进行粗对准（如空中对准）时，都需要考虑在大失准角情况下的初始对准问题[3，4].

近年来，针对SINS大失准角下初始对准的误差模型和非线性估计方法不断涌现，Bucy等[5，6]等提出并研究了适用于非线性系统和非线性量测情况下的扩展卡尔曼滤波（extended Kalman filter，EKF）算法.但EKF引入了高阶项截断误差，必然会降低模型的准确性，随着时间的延长，估计精度难以保证，甚至使滤波器难以稳定.此外，在使用EKF算法前必须知道非线性函数的具体展开形式，才能计算非线性函数的Jacobian矩阵，且此过程非常繁琐并容易出错.Julier等提出了处理非线性问题的无迹卡尔曼滤波 （unscented Kalman filter，UKF）算 法[7，8].UKF的独特之处在于采用确定性采样策略近似非线性分布，取代EKF对非线性模型的线性化处理，避免了求取Jacobian矩阵，能取得更好的滤波性能[9，10].

捷联惯导系统依据载体在初始对准时的运动状态可将初始对准分为两类，即静基座初始对准和动基座初始对准.通常，捷联惯导系统的可观测性较差，尤其在静基座情况下其可观测性最弱；在动基座情况下，通过使基座有目的地机动可以提高捷联惯导系统的可观测性，从而提高捷联惯导系统初始对准的收敛速度及估计精度.本文主要研究静基座情况下，SINS的初始对准问题.基于欧拉平台误差角（EPEA）的概念描述理论导航坐标系到计算导航坐标系之间的失准角[3，11]，摒弃经典小失准角误差模型中无限转动与旋转次序无关的做法.在此基础上推导适用于SINS初始对准的非线性误差模型，该模型对姿态误差和相对姿态不作任何线性化假设，能准确描述SINS的误差传播规律.在系统噪声和量测噪声均为复杂加性噪声并且量测方程为线性方程时，详细分析大失准角、大方位失准角与小失准角情况下初始对准过程的异同，给出带阻尼解算的简化EKF算法和简化UKF算法，并对两种滤波算法在静基座状态下的对准效果进行Monte Carlo[12]仿真比较.

1 SINS的非线性误差模型

1.1 EPEA微分方程

首先定义文中所用到的坐标系：地心惯性坐标系记为i系；地球坐标系记为e系；导航坐标系选取“东 －北 －天”地理坐标系，记为n系；机体坐标系选取“右 －前 －上”坐标系，记为b系[13].n系依次绕航向轴、俯仰轴、横滚轴作3次欧拉角旋转可至b系，且n系到b系的旋转变换关系可用姿态矩阵Cbn描述.实际上，带误差的计算导航坐标系n′系与理想导航坐标系n系之间存在失准角.类似于n系到b系的转动过程，n系依次经过3次基本旋转可至n′系，记这3次旋转的欧拉误差角分别为αz、αx和αy，则其确定的坐标变换矩阵如下：

根据有限次基本旋转的复合原理，n系到n′系的姿态矩阵为

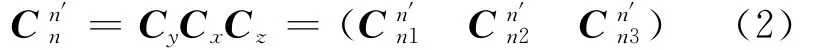
其中

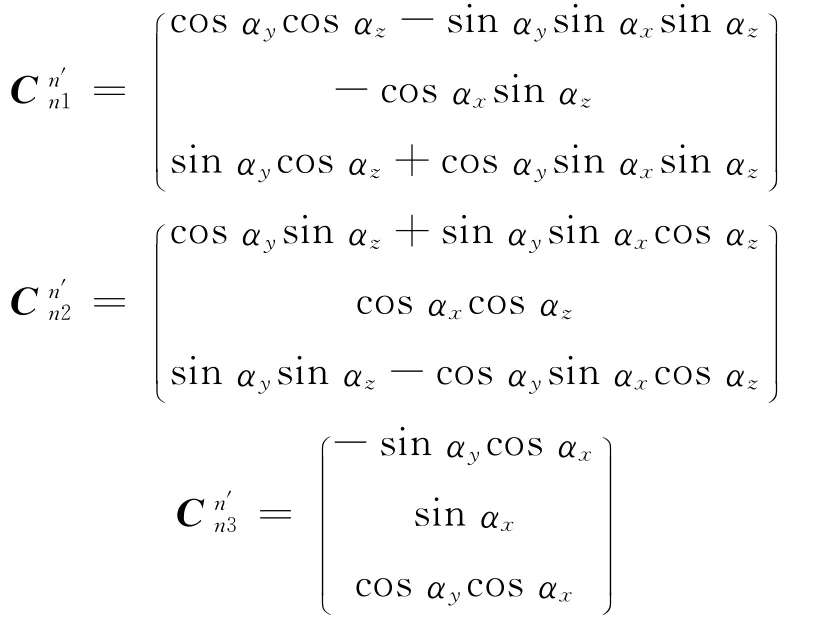
在水平误差角αx和αy较小而方位误差角αz较大的大方位失准角情况下，有

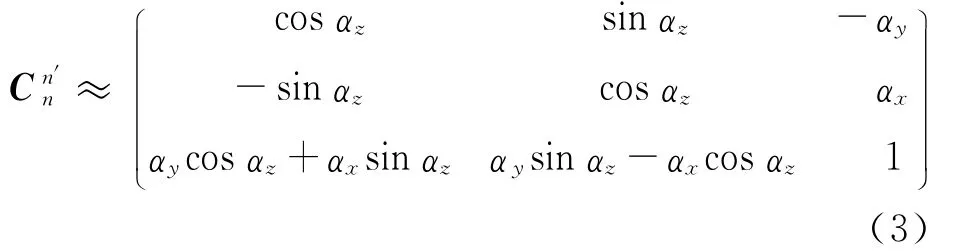
在欧拉误差角均为小角度的小失准角情况下，有

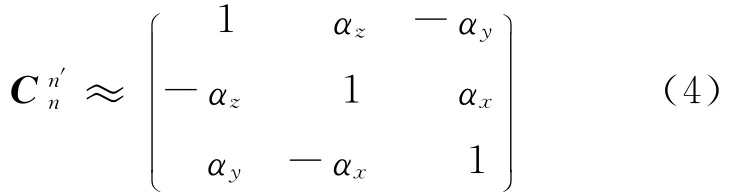
记矢量α＝ （αxαyαz）T，设（Φ×）为由α构造的反对称矩阵，则有

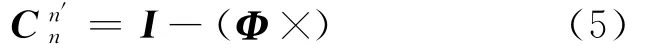
设n′系相对于n系的角速度为

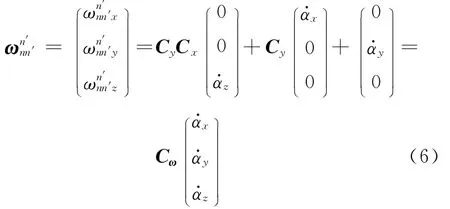
于是，得

式（7）即为欧拉平台误差角微分方程，它描述了欧拉平台误差角α与n′系角速度ωn′nn′之间的关系，若能推导出ωn′nn′的变化规律，则可建立起SINS基于欧拉平台误差角的误差模型.

若水平误差角αx和αy为小角度，ωn′nn′可近似为

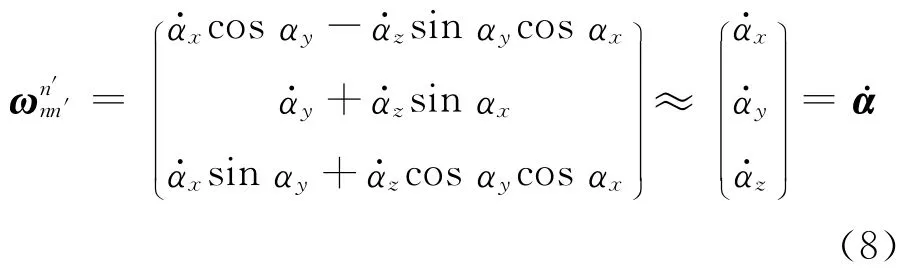
因此，在大方位失准角或小失准角情况下，欧拉平台误差角微分方程可简化为

1.2 姿态误差方程

理论上，SINS在n系的姿态矩阵微分方程为

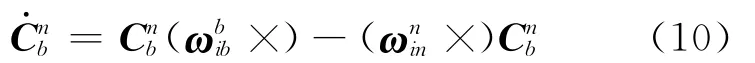
其中（ω×）表示由向量ω构成的反对称矩阵，且

实际上，SINS含误差的姿态矩阵微分方程为

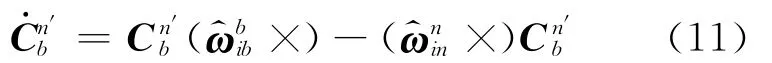
定义姿态矩阵的计算误差

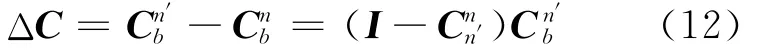
对式（12）求微分，并将式（10）、（11）代入，整理得

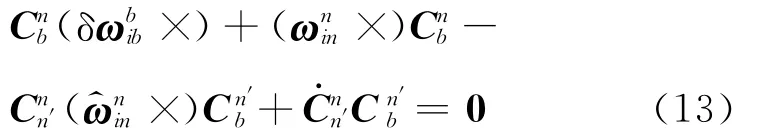
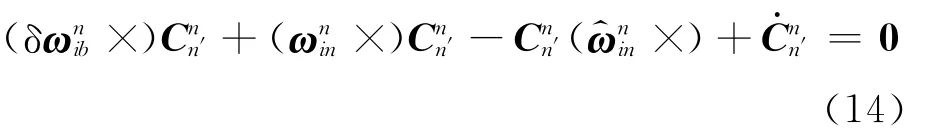
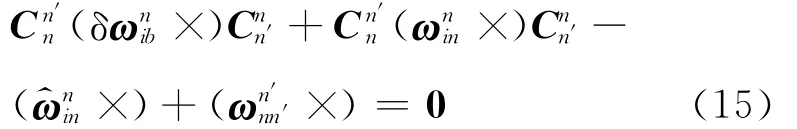
根据反对称阵的相似变换及其与矢量之间的关系，上式的矢量等价形式为

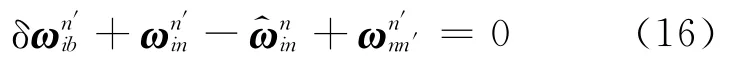
整理得

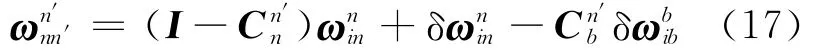
最后，将式（17）代入式（7），得SINS基于EPEA的非线性姿态误差方程

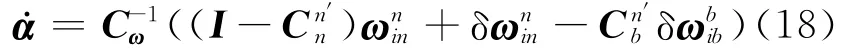
大方位失准角或小失准角情况下，根据式（9）得

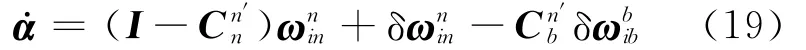
小失准角情况下，根据式（5）得

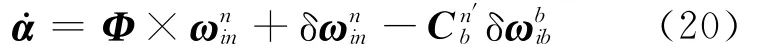
1.3 速度误差模型

理论上，SINS在n系的速度微分方程为

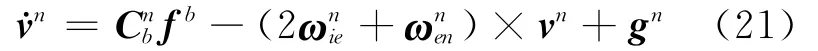
实际上，SINS含误差的速度微分方程为

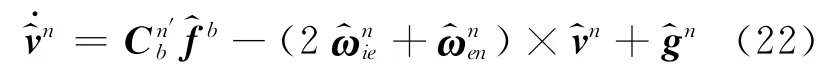
将式（22）和（21）相减，可得SINS速度误差方程

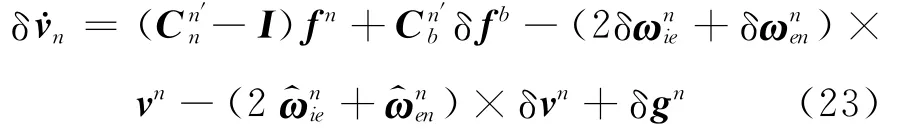
小失准角情况下，将式（5）代入上式得

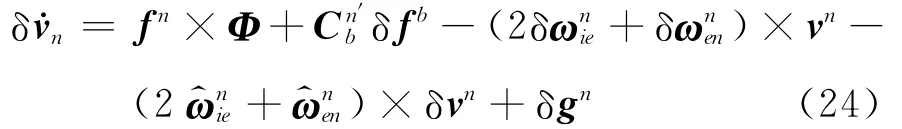
1.4 SINS静基座初始对准方程

静基座状态下SINS的对准过程中，通常假定当地位置已知且固定不变，可以不考虑位置误差的影响，即则SINS大失准角情况下初始对准的非线性方程为

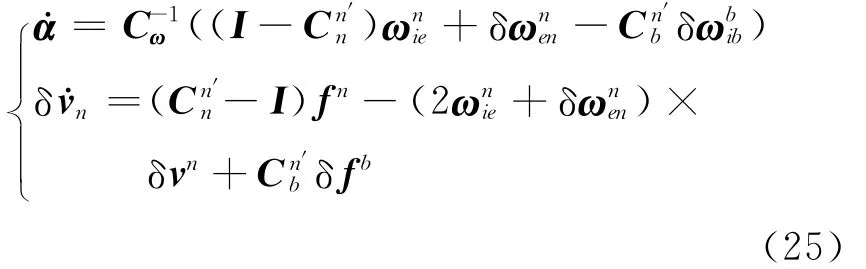
大方位失准角情况下SINS初始对准方程为

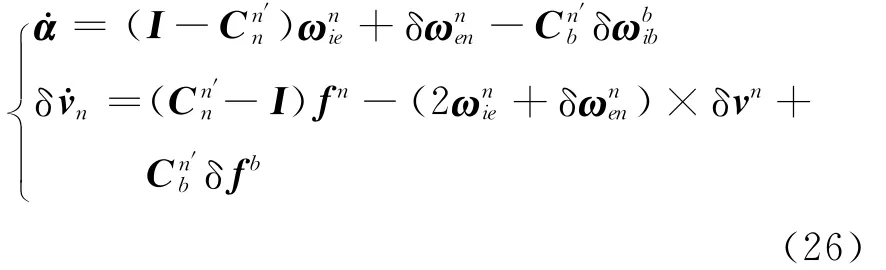
小失准角情况下SINS初始对准方程为

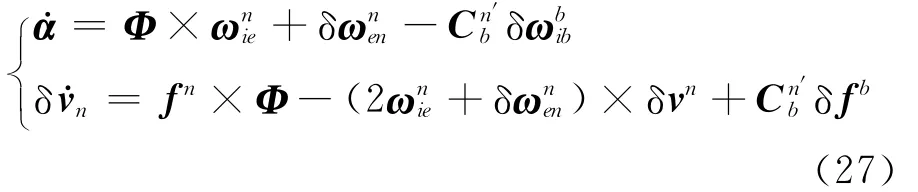
其中非线性函数f（·）、g（·）的具体形式根据失准角的大小情况从式（25）～（27）中解算，量测矩阵Hk＝ （03×3I3×3），vk为量测噪声.

2 EKF算法和UKF算法

EKF与UKF使用的都是标准Kalman滤波器的框架，是回归最小均方误差估计器，但二者实现原理不同.本文研究在系统噪声和量测噪声均为加性噪声并且量测方程为线性方程时，SINS的非线性误差模型.当量测方程是线性方程时，EKF和UKF的滤波递推过程都可得到进一步的简化，从而有利于降低滤波计算量和减小滤波发散可能性.

2.1 EKF算法

与标准Kalman滤波一样，EKF也采用“预测－更新”的算法框架，针对式（28）所描述的非线性系统，其标准递推过程如下.

预测：

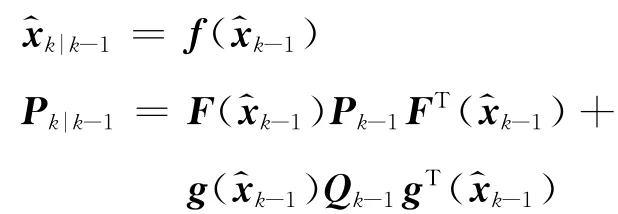
更新：

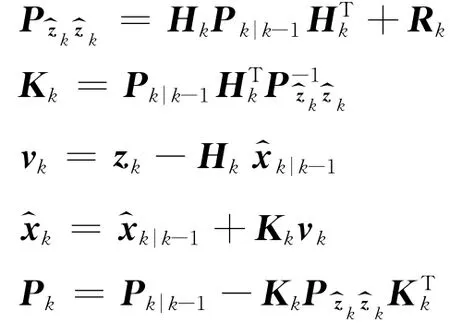
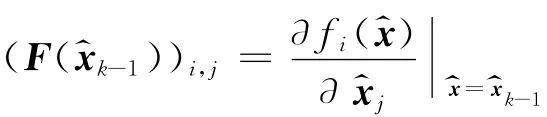
以上是基于非线性离散系统模型进行的EKF递推过程描述，即采用先离散化后线性化的

推导方法.在实际程序中，考虑到系统离散化以及离散化系数矩阵计算的方便，采用先线性化后离散化的推导方法.在Kalman滤波算法的递推过程中，系统均方误差矩阵Pk和Pk｜k－1要求是非负定的.而实际滤波过程中，估计的均方误差矩阵可能会逐渐失去非负定性甚至失去对称性，导致滤波发散，因此需要在数值稳定性方面对标准递推过程做进一步的改进.

2.2 UKF算法

当系统噪声和量测噪声均为加性噪声时，为了降低滤波计算量，无需对其进行状态增广处理[14]，针对式（28）所描述的非线性系统，采用对称采样点策略，简化的UKF递推过程如下.

构造采样点：

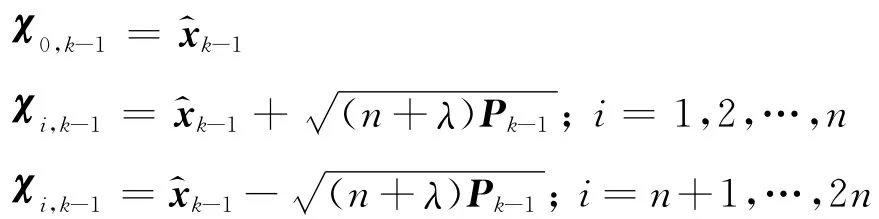
预测：

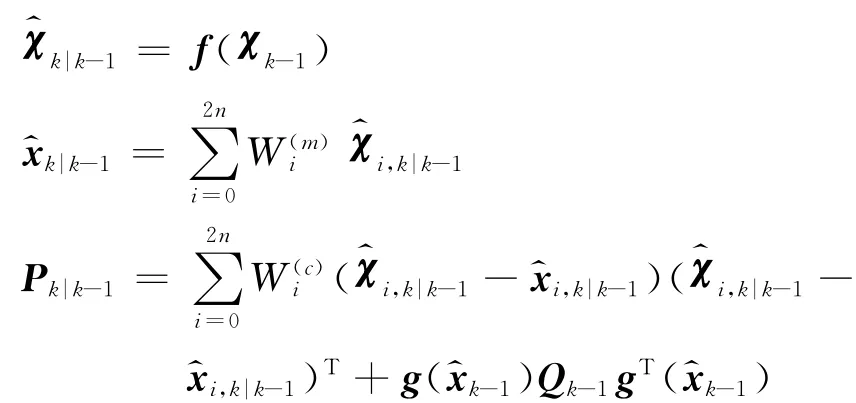
更新同EKF算法的更新.

相应的权重计算如下：

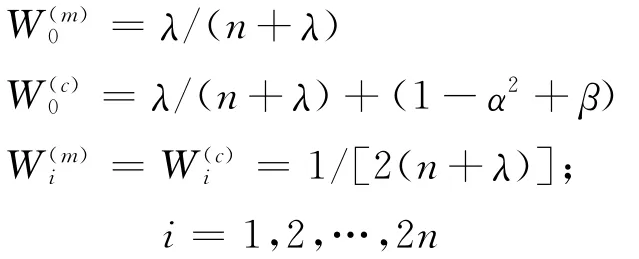
其中n是状态向量xk的维数；λ＝α2（n＋κ）－n是一个比例参数；α控制采样点的分布状态，决定采样点与均值的离散程度，通常取为0到1之间很小的正值，如1×10－3；κ是一个比例因子，在状态估计时通常取为0；β也是一个比例因子，在状态满足Gauss分布时通常取为表示矩阵P的平方根，满足矩阵方程P＝AAT，A可以通过奇异值分解、Cholesky分解、特征根分解等方法求得.

由以上递推过程可知，UKF与EKF一样，都采用标准Kalman滤波器“预测－更新”的算法框架.当系统状态方程为非线性方程而量测方程为

线性方程时，在预测阶段，EKF通过计算Jacobian矩阵进行状态及其均方误差预测，而UKF通过使用UT变换进行状态及其均方误差预测，但二者在更新阶段的滤波步骤与标准Kalman滤波算法完全相同.UKF不对非线性系统方程和量测方程进行线性化，而是对状态向量的概率密度函数进行近似，因此不依赖于非线性系统方程的具体形式，算法相对独立，适用于任何形式的非线性模型.

3 仿真实验

假设SINS所处位置的地理纬度为45°，选取较低精度陀螺的对应值，陀螺仪的常值漂移为0.1°/h，随机漂移为0.01°/h；加速度计的常值偏差为100×10－6g，随机偏差为50×10－6g.选择3种比较典型的初始失准角，即大失准角情况α（0）＝ （10° 20° 60°）T，大方位失准角情况α（0）＝ （1° 2° 60°）T，小失准角情况α（0）＝（10′ 20′ 60′）T.为了比较初始对准算法的性能，在相同条件下分别将EKF算法和UKF算法用于精对准过程，3种情况下Monte Carlo仿真得到的失准角估计误差如图1所示.

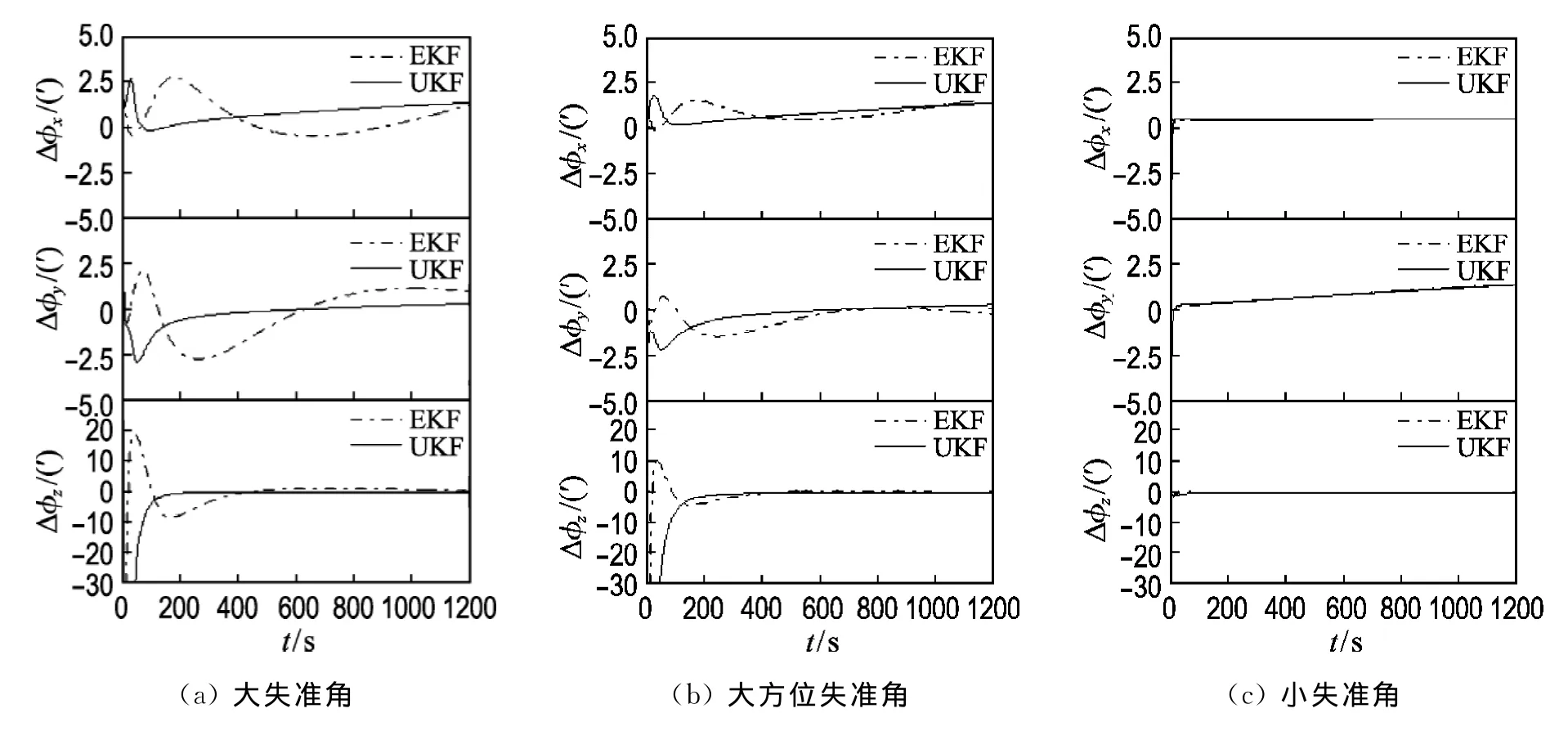
图1 不同失准角估计误差Fig.1 Estimation errors for different misalignment angles

仿真结果表明，不同失准角情况下，采用本文给出的非线性初始对准模型，EKF和UKF算法都能满足对准要求，且初始失准角越小，对准时间越短，对准精度越高.大失准角、大方位失准角情况下，UKF算法较EKF算法具有对准时间更快、对准精度更高和适用范围更广的优点，但UKF算法的计算量比EKF大；而在小失准角情况下，由于系统的线性化误差小，二者的对准时间和对准精度基本相同.

为了更清楚地比较上述两种方法的对准效果，相同条件下分别进行100次Monte Carlo仿真.表1中给出了对准结束前100s内各失准角估计均方根误差对时间的平均值，图2给出了不同失准角下估计均方根误差的分布情况.

表1 失准角的估计均方根误差稳态值Tab.1 Steady－state RMSE of estimated misalignment angles

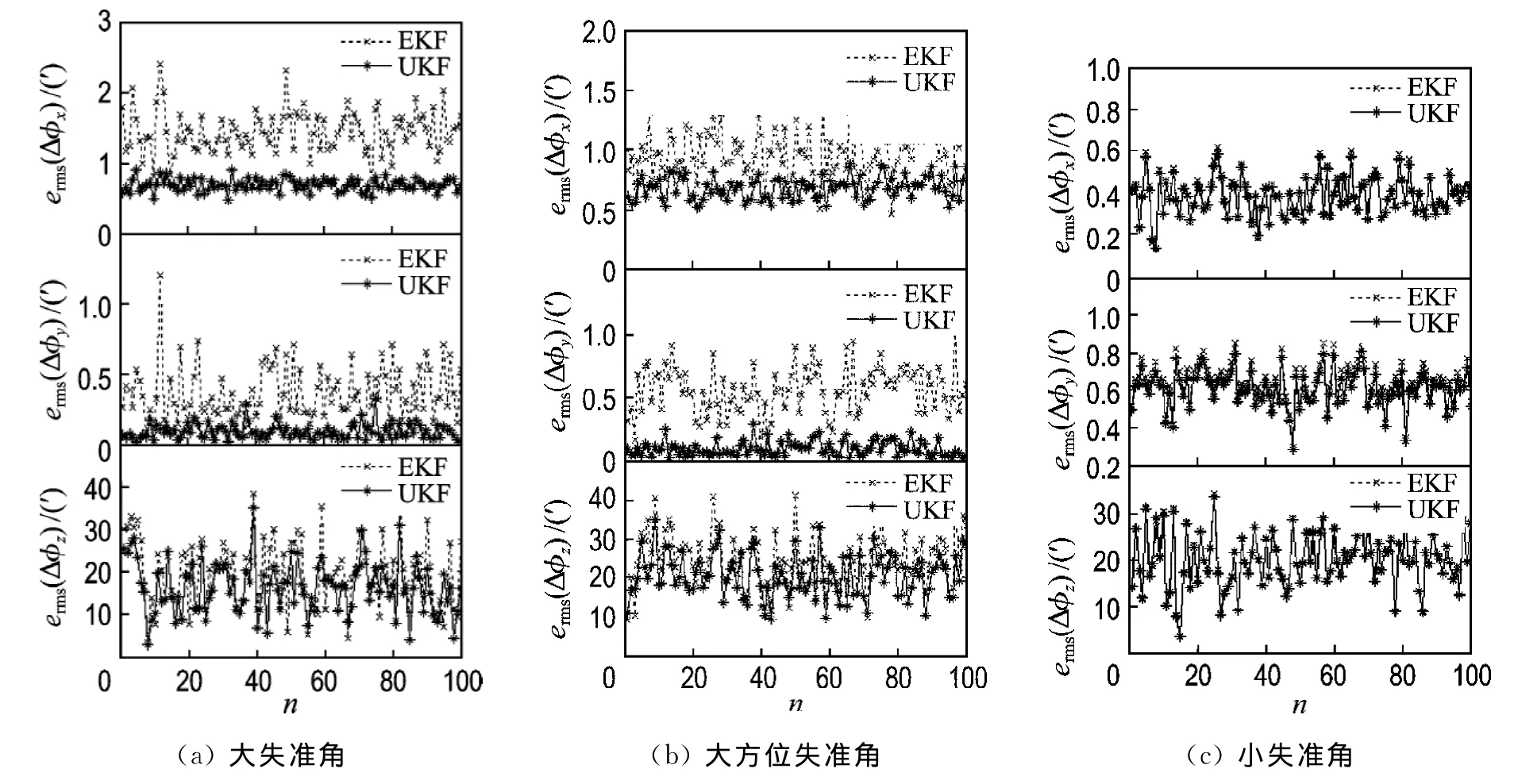
图2 失准角的估计均方根误差分布Fig.2 ermsdistribution for misalignment angles

4 结 语

本文基于欧拉平台误差角的概念建立了SINS在大失准角、大方位失准角与小失准角情况下的初始对准误差模型.在量测方程为线性时，推导了简化的EKF算法和UKF算法，分析了不同失准角情况下初始对准过程的异同.静基座状态下的Monte Carlo仿真结果，验证了基于3种失准角所建立的初始对准误差模型的准确性和两种非线性初始对准算法的有效性，并对两种滤波算法的性能做了定性和定量的评估.

实际上，没有一种滤波算法可以被证明明显地优于其他滤波算法.选择哪一种滤波算法或者哪些滤波算法的组合，最终取决于实际的应用场合和应用目标.在系统线性误差不大，且系统的线性化模型比较容易获得的情况下，比较适合采用EKF算法；而在系统线性误差比较大的情况下，EKF已无法保证良好的估计性能，此时适合采用UKF算法.采用EKF算法和UKF算法的主要目的是为了迅速辨识失准角大致范围并降低初始对准误差，对准过程中当失准角满足小角度假设时，进一步切换到经典小失准角Kalman滤波方法，能在提高对准精度的同时进一步降低计算量，从而获得更为准确的初始姿态矩阵.

[1] JIANG Y F. Error analysis of analytic coarse alignment methods [J].IEEE Transactions on Aerospace and Electronic System，1998，34（1）：334－337.

[2] 秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理[M].西安：西北工业大学出版社，1998.QIN Yong－yuan，ZHANG Hong－yue，WANG Shuhua.Kalman Filter and Integrated Navigation Principle [M].Xi′an：Northwestern Polytechnical University Press，1998.（in Chinese）

[3] 魏春岭，张洪钺，郝曙光.捷联惯导系统大方位失准角下的非线性对准[J].航天控制，2003（4）：25－34.WEI Chun－ling，ZHANG Hong－yue， HAO Shuguang.SINS nonlinear alignment with large azimuth misalignment angles [J]. Aerospace Control，2003（4）：25－34.（in Chinese）

[4] Kim K， Park C G. Non－symmetric unscented transformation with application to in－flight alignment[J].International Journal of Control，Automation and Systems，2010，8（4）：776－781.

[5] Bucy R S，Senne K D.Digital synthesis of non－linear filters[J].Automatica，1971，7（3）：287－298.

[6] Sunahara Y. An approximate method of state estimation for nonlinear dynamical systems [J].Transactions of the ASME.Series D，Journal of Basic Engineering，1970，92（2）：385－393.

[7] Julier S J，Uhlmann J K，Durrant－Whyte H F.A new method for the nonlinear transformation of means and covariance in filters and estimators [J].IEEE Transactions on Automatic Control，2000，45（3）：477－482.

[8] 潘 泉，杨 峰，叶 亮，等.一类非线性滤波器——UKF综述[J].控制与决策，2005，20（5）：481－489.PAN Quan，YANG Feng，YE Liang，etal.Survey of a kind of nonlinear filters— UKF[J].Control and Decision，2005，20（5）：481－489.（in Chinese）

[9] Romanenko A，Castro J.The unscented filter as an alternative to the EKF for nonlinear state estimation：a simulation case study[J].Computers and Chemical Engineering，2004，28（3）：347－355.

[10] Kol s S，Foss B A，Schei T S.Constrained nonlinear state estimation based on the UKF approach [J].Computers and Chemical Engineering，2009，33（8）：1386－1401.

[11] 严恭敏，严卫生，徐德民.简化UKF滤波在SINS大失准角初始对准中的应用[J].中国惯性技术学报，2008，16（3）：253－264.YAN Gong－min，YAN Wei－sheng，XU De－min.Application of simplified UKF in SINS initial alignment for large misalignment angles[J].Journal of Chinese Inertial Technology， 2008，16（3）：253－264.（in Chinese）

[12] Doucet A，De Freitas N，Gordon N.Sequential Monte Carlo Methods in Practice[M].New York：Springer－Verlag，2001.

[13] 秦永元.惯性导航[M].北京：科学出版社，2006.QIN Yong－yuan.Inertial Navigation[M].Beijing：Science Press，2006.（in Chinese）

[14] 刘 也，余安喜，朱炬波，等.加性噪声条件下的UKF算法 [J].中国科学：技术科学，2010，40（11）：1286－1299.LIU Ye，YU An－xi，ZHU Ju－bo，etal.Unscented Kalman filtering in the additive noise case [J].Science China－Technological Sciences， 2010，40（11）：1286－1299.（in Chinese）