自愈合混凝土损伤演化声发射监测及其评价技术

李 冬 生， 匡 亚 川， 胡 倩

（1.大连理工大学 土木工程学院，辽宁 大连 116024；2.中南大学 土木工程学院，湖南 长沙 410083）

0 引 言

混凝土是一种多孔性的脆性材料，作为土木工程结构中应用最广泛的材料，其抗拉强度远远低于其抗压强度，韧性差，对冲击、开裂的抵抗能力差，在外部荷载下，不可避免地产生裂缝.一旦裂缝产生，其防水性降低，导致钢筋腐蚀，混凝土的粘结能力下降，结构的安全性和耐久性将降低.因此，修复混凝土裂缝显得非常必要.自愈合混凝土是对材料损伤破坏具有自行愈合和再生功能，可恢复甚至提高材料性能、增强延性弯曲能力的一种新型复合材料[1].对于混凝土的自愈合行为，它的愈合效果及其服役过程中的损伤演化，目前还缺乏有效的研究手段.寻找一种方法合理地、准确地判断和跟踪愈合效果及其损伤演化，将为自愈合混凝土走向实际工程应用奠定很好的基础.

构件受力作用产生变形或断裂，以弹性波的形式释放应变能的现象称为声发射（acoustic emission，简称 AE）[2].声发射是一种动态、被动监测技术，不像超声那样需借助外界的能量.它能够真正做到在线、实时监测，能快速显示物体的破损状态和缺陷位置，大大节省监测时间、降低成本[3].Georg等[4]基于声发射凯塞 （Kaiser）效应的荷载比和卡姆比等方法得到了混凝土损伤程度等级分类；Santosh等[5]利用声发射事件数和声发射能量研究了混凝土界面断裂行为；吴胜兴等[6]在MTS材料试验机上进行相同尺寸的混凝土、骨料（花岗岩）、砂浆和骨料、砂浆界面4种试件的轴拉试验，利用声发射技术识别混凝土损伤断裂过程的物理机理；朱宏平等[7]利用声发射信号与速率过程理论对混凝土损伤进行了定量评估.从国内外的研究成果来看，声发射技术可以有效地监测混凝土裂纹的产生与扩展.它对构件内部变化非常敏感，混凝土愈合前后由于构件内部变化，在宏观上将表现声发射信号的不同.不扩展的裂纹就不会产生声发射信号，利用有无声发射信号及信号的特征变化，可以判断混凝土自愈合效果及其损伤演化过程，及时提供预警信息，避免灾难性的事故发生.

1 试验方案与加载装置

（1）自修复混凝土的制备

自修复混凝土是根据人体伤口由“破裂—流血—凝结—愈合”的过程，将含有修复剂的修复纤维掺入到混凝土材料中，当混凝土基体出现损伤或裂缝时，纤维胶液管随之破裂，其中的修复胶粘剂流出，修复损伤.具体制备工艺及要求见文献[8].

（2）试验装置与方法

本试验以环氧树脂为修复剂，砂浆为基体材料.试件尺寸为40mm×40mm×160mm，水灰比为0.5，灰砂比为1∶3.

浇注后，在标准养护条件下养护至28d龄期，在Instron8501万能试验机上进行三点弯曲试验（图1、2）.加载速度为0.025mm/min.为了有效监测自愈合混凝土损伤演化和开裂情况，在试件两端各布设一个声发射传感器，距离端部20 mm.在试验过程中，不可避免出现噪声.通过两种办法去除环境噪声，一种是设置门槛值，另一种是设置滤波频率.通过空采和混凝土损伤声发射频率段，声发射试验门槛值设置为45dB，滤波频率为100～600kHz.在试件的初始损伤阶段，声发射信号比较微弱，通过设置增益来提高信号的强度.本试验采取两级增益放大，前置放大增益设置为40dB，主放大增益为20dB.试验过程中，应该不断观察裂纹扩展情况，一旦发现修复剂流出，停止加载.然后等待10d左右，待修复剂完全固化并对裂缝进行了有效的修复，再进行第2次试验.

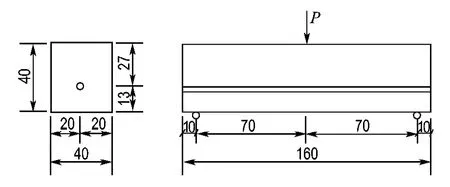
图1 三点弯曲裂缝自修复试验Fig.1 Three point bending experimentation of cracks self－repairing

图2 试验加载装置Fig.2 Load device of experimentation

2 试验结果与讨论

2.1 自愈合混凝土强度回复率

试验测试了修复前后试件的强度，第1次测试（修复胶粘剂释放之前）结果与第2次测试（修复胶粘剂释放，渗入到基体中修复裂缝之后）结果比较如表1所示.从表1可以看到：未经修复胶粘剂修复的试件，在第1次三点弯曲试验后已经破坏，因而在第2次试验时其强度下降了80%～90%，几乎不能再次承受荷载.而经修复胶粘剂修复后的试件第2次弯曲试验时，混凝土平均强度提高了30.6%.这是因为，混凝土出现开裂后，事先埋置在里面的胶粘剂发生破裂，胶粘剂流向裂缝处，使裂缝面重新愈合，试件的承载能力得到提高.第2次加载时，由于修复胶粘剂的粘结能力大于砂浆，裂纹并不在上次出现裂缝的地方开裂，应力分配到别的未开裂的地方，这就是试件强度提高的原因.

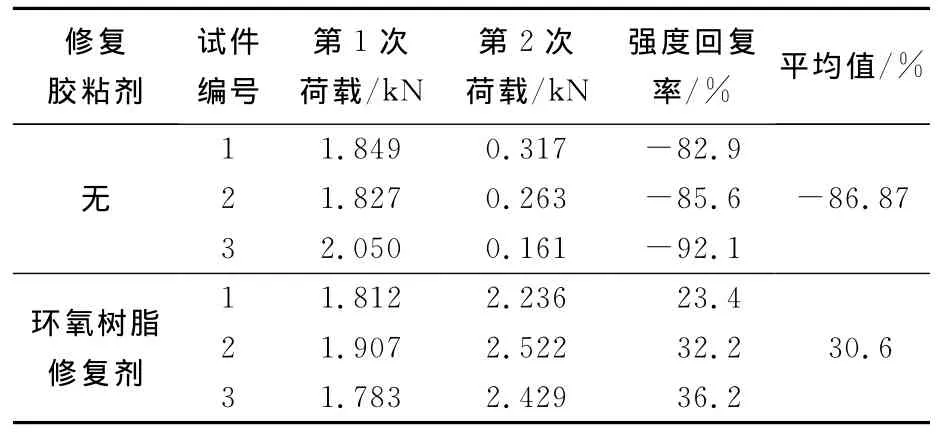
表1 修复前后试件的强度回复率Tab.1 Strength recovering ratio of samples before and after repairing

2.2 自愈合混凝土损伤声发射特征信号

为了得到自愈合混凝土损伤过程的声发射特征，运用声发射技术进行自愈合混凝土破损全过程检测.愈合前后声发射特征参数如图3、4所示.愈合前后的混凝土在加载过程中都产生了丰富的声发射信号.随着荷载的增加，声发射信号逐渐变大.这种变化现象不符合声发射凯塞效应.这是因为在这次试验之前的加载中，尽管混凝土已经产生了裂缝，但埋在混凝土中的内置纤维胶液管随着混凝土的开裂而断裂，修复胶粘剂迅速流出，混凝土裂缝重新修复，使混凝土变得完好如初.因而在进行自愈合效果验证试验时，愈合后的混凝土跟愈合前的混凝土发生了类似的损伤过程.其声发射监测结果也说明了这一点.具体损伤过程为，在加载初期，声发射事件数随着时间增加变化不大，这是因为混凝土是一种多孔材料，在外部荷载的作用下，内部微小孔洞被压实，压实过程中，砂浆颗粒相互摩擦和碰撞，产生小量的声发射信号.此后，随着荷载的增加，声发射计数增加得越来越明显，这说明试件内部开始发生了变化，产生了微裂缝；在试验进行到180s之后，荷载达到最大值，声发射特性参数变化非常剧烈，其特征参数值急剧增加.这是因为混凝土为一种脆性材料，荷载达到最大值之后，裂缝出现不稳定扩展，试件发生脆性断裂.

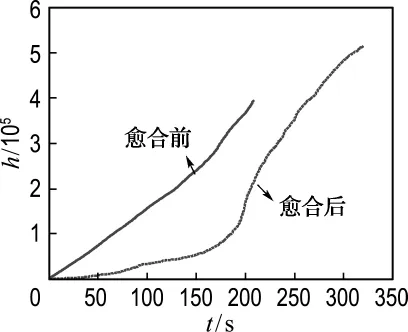
图3 声发射传感器累积计数变化曲线Fig.3 Evolution of acoustic emission hits recorded by transducers

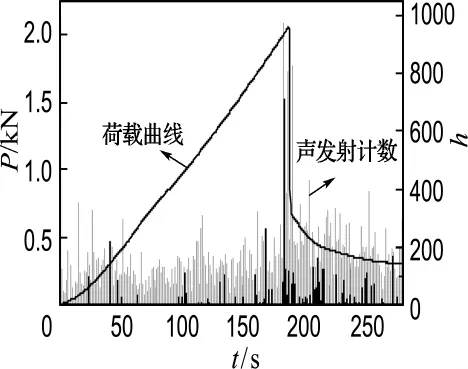
图4 自愈合混凝土声发射计数与荷载曲线Fig.4 Load and AE hits for self－repairing concrete

从图4还可以看出，声发射计数变化曲线和荷载曲线同步变化，具有良好的对应关系.在荷载的最大值处，声发射计数达到最大值，声发射信号变化更加剧烈.因此可以利用声发射计数包络曲线代替荷载曲线，定性地揭示试件的破坏情况.

2.3 声发射费利西蒂（Felicity）比与混凝土愈合效果比较

从图3愈合前后的声发射计数图可以看出，自愈合混凝土不符合声发射凯塞效应，重新加载声发射信号出现的时刻早于预定时刻，即荷载并未达到前一次加载的最大值已产生新的信号，这种现象称为费利西蒂（Felicity）效应.Felicity比定义为第i＋1次加载过程中出现的第一个声发射信号对应的荷载与第i次加载过程中的最大荷载之比.它反映了加载历史对材料或结构的影响.但在试验现场，由于各种环境及试验过程产生的噪声，即使试件没有发生损伤，声发射仪器也可能接收到信号.因此如何判断是不是有效声发射信号，显得很重要.本文根据纪洪广等[9]提出的方法来进行Felicity比的计算，结果见表2.

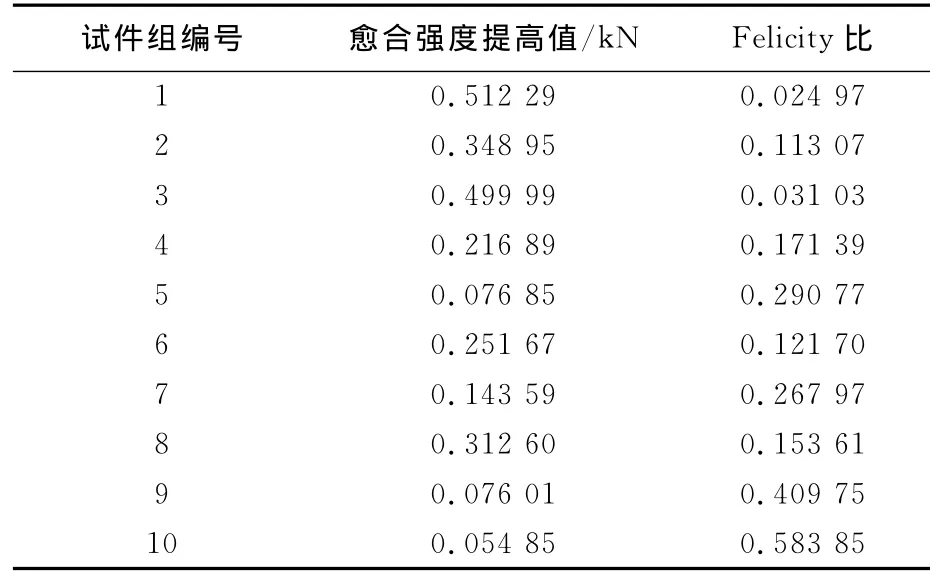
表2 混凝土愈合强度与Felicity比Tab.2 Repairing strength of concrete and Felicity ratio

从表2可以看出：Felicity比随着愈合强度的提高而减小.这是因为试件经过预加载，内部产生了微裂缝，修复剂流向断面处，使它得到了及时的修复，试件的强度得到了改善.等到第2次加载时，根据微裂缝面粘结的好坏，如果粘结处的强度大于原来的强度，将在试件别的地方产生微裂缝，如果低于原来的强度，微裂缝面将发生二次开裂.这样，就表现出了Felicity效应.因此，利用Felicity效应可以判断愈合效果的优劣，至于Felicity比跟愈合效果优劣是否有定量的关系，有待进一步研究.

3 基于小波分析技术自愈合混凝土损伤演化分析

声发射信号是典型的非平稳信号，经典的傅里叶变换不适合分析这类信号，而小波分析技术能够在时频上同时进行信号分析，非常适合非平稳信号分析.通过对声发射信号进行小波分析，提取相关特征参数、寻找信号突变点，能有效地判断自愈合混凝土的损伤演化.这是因为，不同损伤类型的声发射信号在时域上（如幅值）、频域上（如频率）具有不同的信号特征，而且不同的损伤阶段，小波分解系数会出现一些突变点.根据这些突变信号的变化，可以有效划分信号的不同损伤阶段.

3.1 小波分解奇异性检测理论简介

一般地，信号的奇异性大小可用Lipschitz指数来描述，也称奇异性指数[10，11].设有非负整数n，n≤a≤n＋1，如果存在常数A＞0，以及n次多项 式pn（t），对 于t∈ （t0－δ，t0＋δ）使则称f（t）在t0数），是Lipschitza的，如果f（t）在t0的Lipschitz指数a小于1，则称t0为f（t）的奇异点.对于小波分析而言，在小波变换中，局部奇异性可定义为设f（x）∈L2（R），若f（x）对x∈δx0，小波φ（x）满足连续可微，并且具有n阶消失矩（n为正整数）有（K为常数），则称a为x0点的奇异性指数（也称Lipschitz指数）.

基于上述小波奇异性检测原理，对声发射特征信号进行小波分解.为了确保划分的准确性，同时结合声发射技术、能量、幅值等参数综合判断其损伤演化状况，本文选取声发射计数进行小波分解和奇异性分析.小波母波选用紧凑型的db3，综合采样频率和分解精度，分解阶次定为5次.为了节省篇幅，本文仅给出第5次分解的声发射计数与时间细节图（图5）.

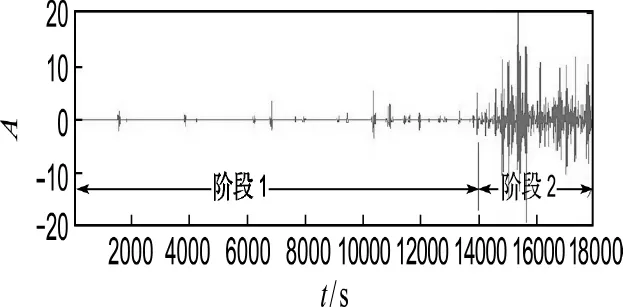
图5 声发射计数小波分解细节图（d5）Fig.5 Wavelet decomposition detail of AE hits at level 5

图5小波分解的结果显示，不同的损伤阶段，其声发射特征参数相差比较大，而且出现了较多的信号奇异点，这表明自愈合混凝土整个加载过程中损伤非常丰富.但总体上看，声发射计数小波分解信号明显分为两个不同的阶段，第一阶段信号比较少，第二阶段声发射信号非常丰富，有效验证了利用小波分解系数奇异检测方法能够准确刻画不同的损伤阶段.基于不同的损伤阶段，可以进一步提取不同损伤的声发射信号，运用小波时频分析技术，确定不同损伤阶段的声发射信号特征.

3.2 自愈合混凝土损伤演化声发射波形小波分析及其损伤类型判定

（1）阶段1自愈合混凝土损伤声发射波形特征

这个阶段的声发射出现了波形1、波形2两种波形，如图6所示；基于小波变换的时频关系如图7（a）、（b）所示.

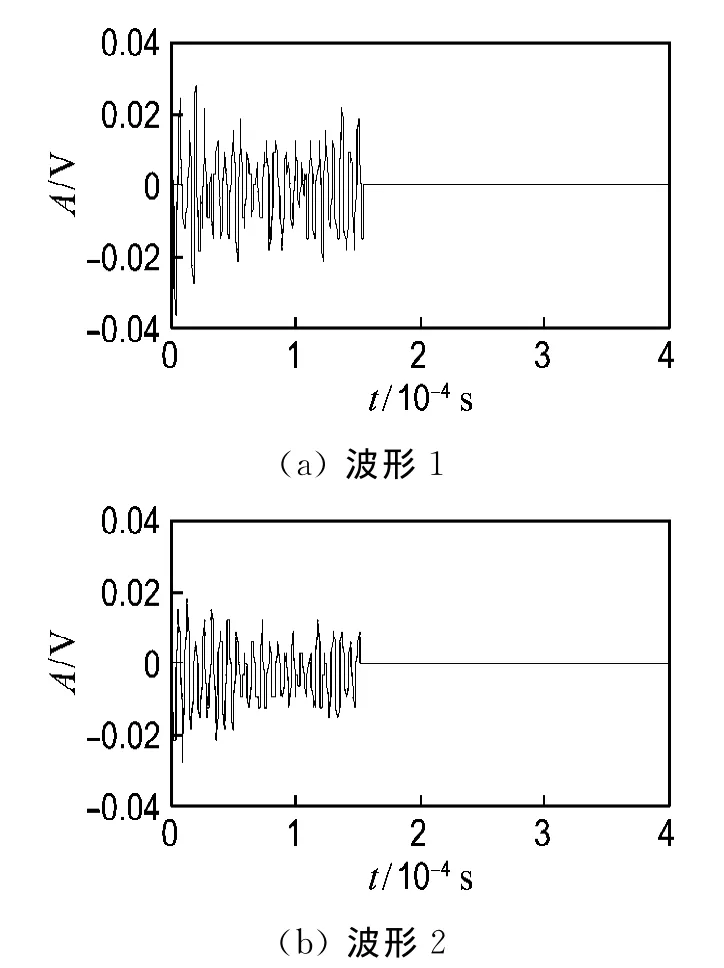
图6 自愈合混凝土阶段1声发射特征波形Fig.6 Acoustic emission waveforms of self－repairing concrete of Stage 1damage

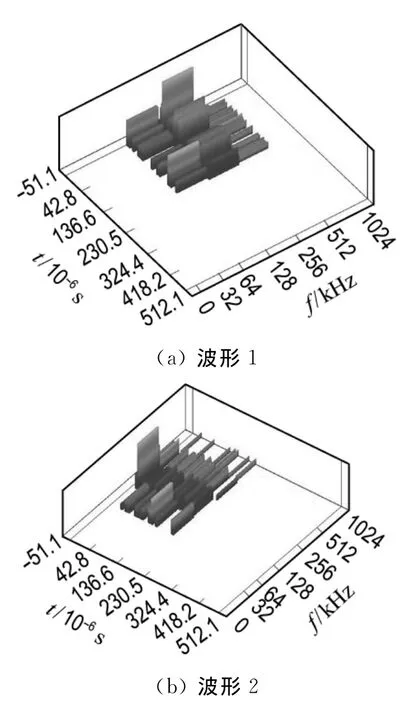
图7 波形1、2时频分析Fig.7 Time－frequency analysis of waveforms 1，2

从图5可以看出，在整个过程中都有声发射信号产生，阶段1的信号表现出很大的离散性，信号大致都保持在一个较小的区域内，发展较为平稳，这个阶段的声发射以波形1为主，信号波形为中低幅度脉冲，如图7（a）所示，其频域分布范围较窄且频率较低，大部分集中在125～250kHz，这是因为自愈合混凝土水泥砂浆被压实，砂浆颗粒相互挤压与摩擦，从而导致了声发射信号的产生.在阶段1中，也出现了少量的突发型信号，但幅值都较低，其声发射为波形2，信号波形为中低幅度脉冲，如图7（b）所示，其频域分布相对较宽，最高可达1 024kHz.这是因为自愈合混凝土是一种多相材料，其内部存在着许多天然的微孔隙和微裂纹，这些缺陷在荷载作用下演化发展，相互融合增长，不断扩展，从而导致了突发型信号的产生.

（2）阶段2自愈合混凝土损伤声发射波形特征

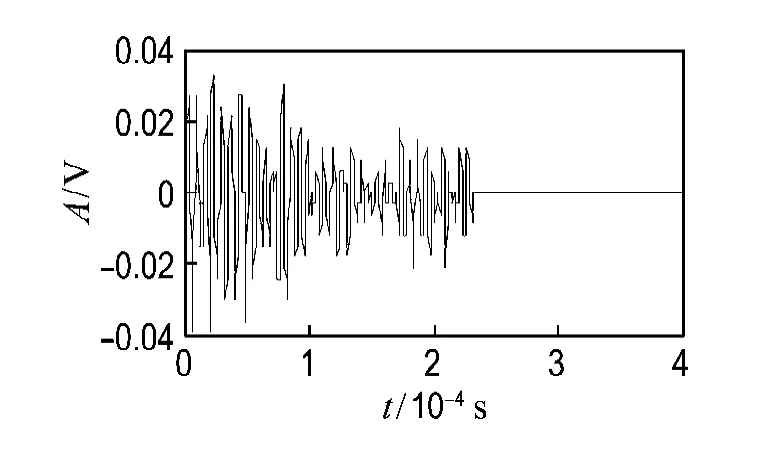
图8 阶段2声发射特征波形Fig.8 Acoustic emission characteristic waveform of Stage 2

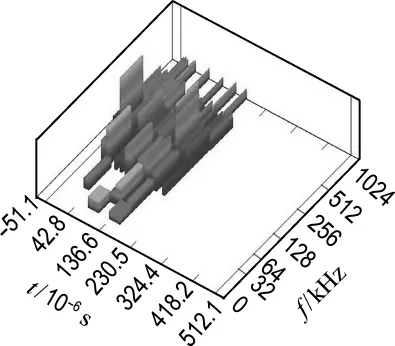
图9 阶段2声发射特征波形时频分析Fig.9 Time－frequency analysis of acoustic emission characteristic waveform of Stage 2

从图5可见，这个阶段的声发射事件数增加得越来越明显，信号密集且幅值较大，其声发射信号波形如图8所示，基于小波变换的时频关系如图9所示.这个阶段的信号波形为高幅度脉冲，与阶段1相比，其频域范围较宽，在32～1 024 kHz内都有分布，大部分集中在128～512kHz的范围，最高可达1 024kHz.说明试件内部开始发生了明显的变化，观察试件，发现它产生了明显的裂缝并出现不稳定扩展，也就是说，阶段2是裂缝的快速扩展阶段.宏观裂缝的产生是这个阶段声发射信号的主要来源.

4 结 论

（1）自愈合混凝土极限承载力比普通混凝土大约提高30%.声发射特征参数能够准确表征自愈合混凝土的损伤变化.随着损伤的加剧，声发射特征参数幅值越来越大，变化更加剧烈.此外，声发射特征参数变化曲线和荷载曲线具有同步变化关系.

（2）运用凯塞效应和Felicity效应能够直观地判断愈合效果的好坏.愈合效果越好，Felicity效应越明显；愈合效果越差，凯塞效应越明显.

（3）对声发射特征参数进行小波奇异分解，能够更准确划分不同的损伤阶段.对不同损伤阶段的声发射波形进行小波时频分析，发现声发射波形随着损伤程度的增加，其幅值变大，频率变宽.不同的损伤阶段其声发射信号具有较大的差异.

[1] Carolyn D.Matrix cracking repair and filling using active and passive modes for smart timed release of chemicals from fibers into cement matrices[J].Smart Materials and Structures，1994，3（2）：118－123.

[2] Yuyama S，Yokoyama K，Niitani K，etal.Detection and evaluation of failures in high－strength tendon of prestressed concrete bridges by acoustic emission[J].Construction and Building Materials，2007，21（3）：491－500.

[3] Philippidis T P， Assimakopoulou T T. Using acoustic emission to assess shear strength degradation in FRP composites due to constant and variable amplitude fatigue loading[J].Composites Science and Technology，2008，68（3－4）：840－847.

[4] Georg K K，Thomas V.Classification of the damage condition of preloaded reinforced concrete slabs using parameter－based acoustic emission analysis [J].Construction and Building Materials，2010，24（12）：2332－2338.

[5] Santosh G S，Chandra K J M.Fracture behavior of concrete－concrete interface using acoustic emission technique [J]. Engineering Fracture Mechanics，2010，77（6）：908－924.

[6] 吴胜兴，王 岩，沈德建.混凝土及其组成材料轴拉损伤过程声发射特性试验研究[J].土木工程学报，2009，42（7）：21－27.WU Sheng－xing， WANG Yan， SHEN De－jian.Experimental study on acoustic emission characteristics of the damage process of concrete and its components under uniaxial tension [J].China Civil Engineering Journal，2009，42（7）：21－27.（in Chinese）

[7] 朱宏平，徐文胜，陈晓强，等.利用声发射信号与速率过程理论对混凝土损伤进行定量评估[J].工程力学，2008，25（1）：186－191.ZHU Hong－ping， XU Wen－sheng，CHEN Xiaoqiang，etal.Quantitative concrete damage evaluation by acoustic emission information and rate－process theory [J].Engineering Mechanics，2008，25（1）：186－191.（in Chinese）

[8] 匡亚川.具有裂缝自修复功能的智能混凝土及其结构构件研究[D].哈尔滨：哈尔滨工业大学，2006：54－56.KUANG Ya－chuan.Smart concrete and structural member study of damage self－repairing of smart concrete [D]. Harbin： Harbin Institute of Technology，2006：54－56.（in Chinese）

[9] 纪洪广，李造鼎.混凝土材料凯塞效应与Felicity效应关系的试验研究[J].应用声学，1997，16（6）：30－33.JI Hong－guang，LI Zhao－ding.Experimental study on the relationship of Kaiser and Felicity effect in concrete material [J].Applied Acoustics，1997，16（6）：30－33.（in Chinese）

[10] MA X， Peyton A J. Feature detection and monitoring of eddy current imaging data by means of wavelet based singularity analysis[J].NDT and E International，2010，43（8）：687－694.

[11] 向 阳，蔡悦斌.小波分析在信号奇异探测及瞬态信号检测中的应用[J].振动与冲击，1997，16（4）：23－30 XIANG Yang，CAI Yue－bin.Application of wavelet transform in singularity detection and transient analysis[J].Journal of Vibration and Shock，1997，16（4）：23－30.（in Chinese）