基于ansys深沟球轴承有限元的分析
2012-05-30常粉玲唐豫桂
王 玲,常粉玲,唐豫桂
(河南农业大学 机电工程学院,河南 郑州 450002)
滚动轴承是广泛应用的机械支承,一般由内圈、外圈、滚动体和保持架组成。向心球轴承是最常用的一类滚动轴承,适用范围宽,生产批量大。它主要用于承受径向载荷,轴承摩擦系数小,适宜于高速运转,且内部结构简单,易于达到较高的制造精度。影响轴承寿命的主要因素是接触疲劳和磨损,而这2种失效又与接触应力密不可分。
在实际工作中,轴承的负荷分布是一个静不定问题,因此采用有限元分析方法会有比较好的效果,为此,采用ansys有限元分析软件建立深沟球轴承的有限元分析模型并尽量模拟其工作时的受载情况进行加载求解,以得到比较有效的静力学接触分析结果。
1 向心轴承中径向载荷的分布情况
轴承工作时,各个元件上所受的载荷及产生的应力是时时变化的。当滚动体进入承载区后,所受载荷即由0逐渐增加 Q2φ、Q1φ,直到最大值 Qmax,然后再逐渐减低到Q2φ、Q1φ直至0。滚动轴承工作时,可以是外圈固定、内圈转动,也可以是内圈固定、外圈转动。对于固定套圈,处于承载区内的各接触点,按其所在位置的不同,将受到不同的载荷。处于Qmax作用线上的点将受到最大的接触载荷,对于每一个具体的点,每当一个滚动体滚过时,便承受一次载荷,其大小是不变的,也就是承受稳定的脉动循环载荷的作用[1-2],如图1所示。
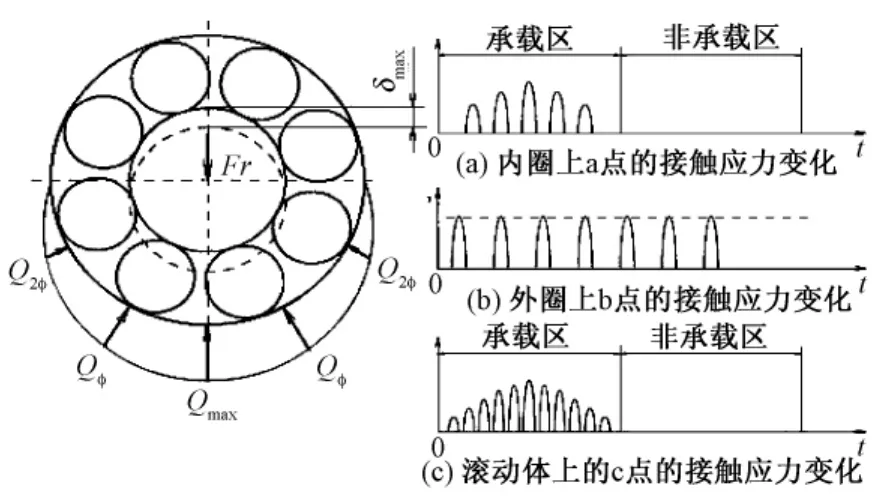
图1 滚动轴承元件承受变化的接触应力
2 接触问题的经典理论
赫兹理论是赫兹1881年求得的关于接触应力和变形的求解问题的经典理论,直到现在还在被广泛使用。在他的分析中,采用了下列假设:接触物体只产生弹性变形,并服从胡克定律;负荷垂直于解除表面,即是接触表面完全光滑,不计摩擦;接触面的尺寸与接触物体表面的曲率半径相比是很小的。半径为R1、R2的2个球体相互接触,在压力P的作用下,形成一个半径为a的圆形接触面,即
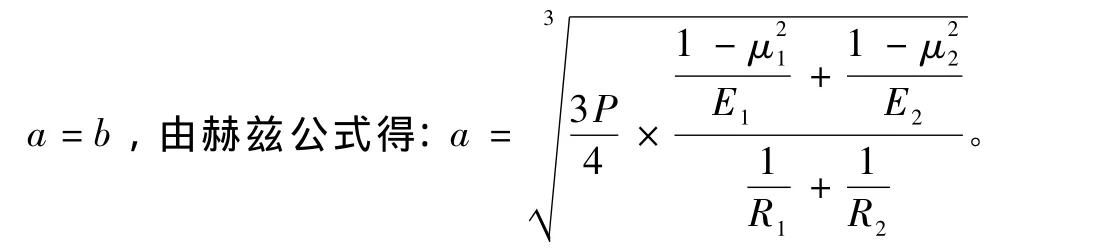
其中,E1、E2为2球体的弹性模量,μ1,μ2为泊松比。
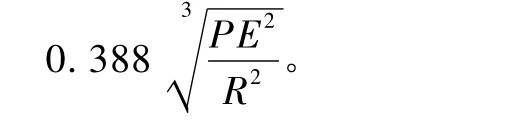
当球面与平面接触时,取 R2趋近于无穷大,R=R1,带入式中可得接触应力[3-6]。
但是当轴承的沟曲率半径系数 fi<0.6时,由赫兹理论所计算出的结果与实际情况的误差开始变大[7],不能满足分析精度需要,此时,采用有限元法计算会有好的效果。
3 建模、约束条件、施加载荷和求解
3.1 有限元模型的建立
深沟球轴承结构如图2所示,以型号为61801的轴承进行分析,其外径21mm,宽度5mm,将轴承在三维软件solidworks中生成此轴承的模型,通过ansys的导入功能导入到ansys中进行分析。

图2 轴承的结构
选择SOLID45作为分析的单元类型,定义材料属性时,取弹性模量E=2.1×1011N·m2,泊松比PRXY=0.3,摩擦因数M=0.2,用扫掠网格划分命令,分别对轴承的内外圈和滚珠进行网格划分,轴承中可能接触的部分要进行细化。共生成147025个节点,306367个单元 (图3)。
3.2 创建接触对
在涉及到2个边界的接触问题时,一般一个设为目标面,另一个设为接触面。对于三维的接触对,使用 TARGE170和 CONTA173,CONTA174,CONTA175,或是CONTA176来组成。每一个接触对都是通过相同的实常数号来识别的。

图3 轴承模型及网格的划分
当指定表面时,参考以下几点:如果是凸面与平面或是凹面接触,那么平面或是凹面要设为目标面;如果一个面的网格划分较密,而相对来说,另一表面网格较粗,那网格划分密的为接触面,网格划分粗糙的为目标面;如果一个面比另一个硬,那么较软的面为接触面,较硬的面为目标面;如果高阶单元覆盖于某一外表面,而低阶单元覆盖于另一外表面,那么覆盖有高阶单元的表面应该设为接触面,而另一面设为目标面,然而,对于三维的点对面接触来说,覆盖低阶单元的表面应该设置为接触面,覆盖有高阶单元的应该设置为目标面;如果一个表面明显大于另一表面,比如一个表面包含另一表面,那么大的表面设为目标面[3,8-12]。
作者利用接触向导设置2个接触对,分别是轴承外圈的内表面和滚珠的接触对1和轴承内圈的外表面和滚珠的接触对2,在2个接触对中都定义滚珠为目标面,弧面为接触面 (图4)。

图4 定义的轴承接触
3.3 施加约束和载荷
将轴承外圈外表面施加3个方向的全约束,将滚动体与内外圈接触点连线的节点进行位移约束,在柱坐标下约束这些节点的切向 (UY)和轴向(UZ)的位移约束。
轴承上半部分所受的力很小或基本不受力,在轴承内圈下半部分施加按照余弦变化的力F=Fmaxcosα,其中Fmax=1000 N,α为轴承受力点与载荷最大处的圆弧所对的圆心角的大小。
3.4 有限元分析结果
通过ansys后处理分析,此轴承在径向载荷作用下各个部位的 Mises等效应力云图如图5所示。图5中可以清晰的显示,在轴承的正下方的滚珠和与之相接触的内外圈受力最大,这与实际状况相符。轴承在Y方向上产生一致的负变形,表示内圈整体下降。不难看出,虽然外载荷只出现在轴承内圈的下半部分,但其上半部分仍然出现较大的向下变形。
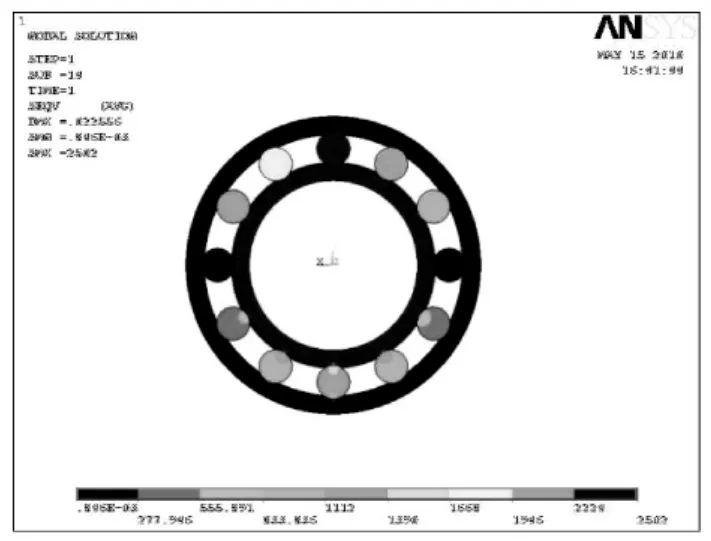
图5 轴承的应力
4 小结
针对高速、轻载基本特征,以ANSYS为开发工具,确定了高速轻载轴承接触分析中的接触方式和接触算法,建立了深沟球轴承有限元计算模型。
对应力计算结果分析可知,滚子与滚道间的接触应力是影响低速深沟球轴承使用的重要因素,且轴承应力最大部位为轴承内圈和所受径向力方的滚珠。
对轴承最大受力部分的分析可以为以后的各项研究工作提供一个参考。
[1]邓凡平.ANSYS10.0有限元分析自学手册 [M].北京:人民邮电出版社,2007.
[2]濮良贵,纪名刚.机械设计 [M].北京:高等教育出版社,2001.
[3]周宁,冼进.ANSYS机械工程应用实例 [M].北京:中国水利水电出版社,2008.
[4]臧新群.汽车滚动轴承应用手册 [M].北京:机械工业出版社,1997.
[5]刘相新,孟宪颐.ANSYS基础与应用教程 [M].北京:科学出版社,2006.
[6]万长森.滚动轴承的分析方法 [M].北京:机械工业出版社,1985.
[7]高霁,苏新伟,钟佳丽.Hertz理论在球轴承应用方面的局限性 [J].轴承,2008(11)9-11.
[8]王大力,孙立明,单福兵.等.ANSYS在求解轴承接触问题中的应用 [J].轴承,2002(9):1-4.
[9]苗学问,王大伟,洪杰.滚动轴承寿命理论的发展 [J].轴承,2008(3):47-52.
[10]吴云鹏,孙立红.滚动轴承力学模型的研究及其进展[J].煤矿机械,2004(2):5-7.
[11]马星国,孙雪,尤小梅.基于ANSYS滚针轴承的有限元分析 [J].中国工程机械学报,2008(9):328-333.
[12]杨巍,罗继伟.关于深沟球轴承沟曲率半径的一点注记[J].轴承,2005(5):1-2.
