各向异性阻抗面电磁散射快速数值算法研究

余定峰 何思远 张 凡 朱国强 殷红成 邓方顺

(1.武汉大学电子信息学院，湖北 武汉 430072； 2.中国航天科工集团公司二院207所，北京 100854； 3.中船重工集团722研究所，湖北 武汉 430079)

引 言

采用吸波材料实现目标雷达散射截面(RCS)的缩减在军事领域具有重要的意义，在雷达电子对抗中有着广阔的应用前景。

三维各向异性材料涂覆目标的电磁散射有两种建模方法，一种仍然以介质涂覆目标为建模对象，应用非常广泛，但在处理高频绕射等问题时碰到困难。耿友林等[1]采用解析法研究了各向异性铁氧体介质涂覆导体球的电磁散射，陈博韬等人[2]采用物理光学法与有限元法混合方法研究了各向异性材料部分涂覆导体的散射特性，毛仕春等人[3]研究了二维各向异性椭圆柱的电磁散射，但都采用张量磁导率或介电常数模拟各向异性材料。另一种则将材料涂覆目标等效为阻抗表面来建模，用阻抗边界条件分析其电磁散射特性，灵活性更强。Senior等[4]在阻抗面电磁散射方面做了大量前瞻性工作，是我们研究工作的基石。Pelosi等[5]提出一种物理光学方法，用于分析各向异性阻抗平面目标的散射，但高频方法适用于电大尺寸问题，且未作非平面结构目标表面各向异性方面的研究。文献[6]提出了各向异性阻抗面电磁散射问题的矩量法(MoM)解决方案，但随着目标电尺寸的增大，极大的计算量和内存需求往往超出计算机的承受能力。

多层UV方法[7-9]直接针对MoM的相互作用矩阵进行快速多层分解，其基于电磁相互作用的排序抽样算法有效解决了因积分核震荡导致UV分解失效的问题，且采用了相互作用矩阵快速填充技术，使内存和时间复杂度均达到O(NlogN).本文基于多层UV矩阵分解技术，应用MoM结合阻抗边界条件(IBC)研究了各向异性阻抗面的电磁散射。根据表面等效原理，采用感应电磁流以RWG矢量基函数展开的伽略金矩量法[10]，得到矩阵方程以后，对相互作用矩阵进行多层分层，得到大量的低秩矩阵块，采用UV分解技术进行处理，再利用稳定的双共轭梯度(BICGSTAB)迭代求解电流，即可解决该各向异性阻抗面电磁散射问题。

1 各向异性MoM原理

如图1所示，在目标表面的小面元上建立局部参考坐标系(x,y,z)，其中：x,y为目标表面的两个切向单位矢量；z为外法线方向单位矢量。目标表面的各向异性光轴方向矢量设为u和v，其中u轴与x轴夹角为光轴偏角ξ.

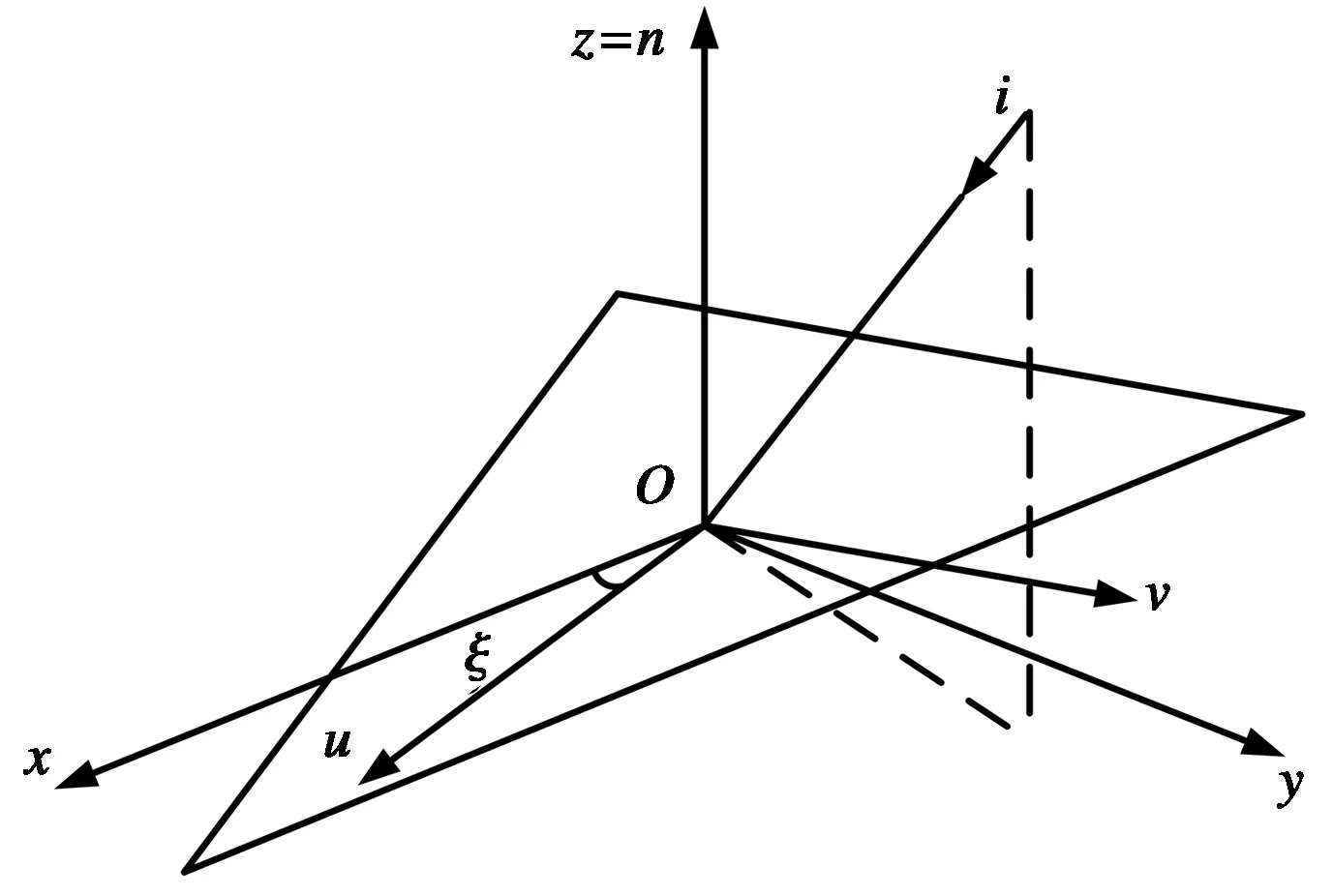
图1 平面波照射各向异性目标表面

(1)

式中：η11=Zucos2ξ+Zvsin2ξ；η22=Zusin2ξ+

Zvcos2ξ；η12=η21=(Zu-Zv)sinξcosξ；Z0为自由空间波阻抗。

Leontovich阻抗边界条件可表示为

(2)

根据等效原理，薄层介质涂覆导电目标可等效为分布于目标表面的电流源J和磁流源M散射电磁场的问题。该等效源满足

J=n×H，M=E×n

(3)

依据散射叠加定理得

E=Ei+Es

(4)

联立式(2) ～(4)得

(5)

(6)

表面电场积分公式为(略去时谐因子ejωt)

Es=-jkZ0A-φe-×F

(7)

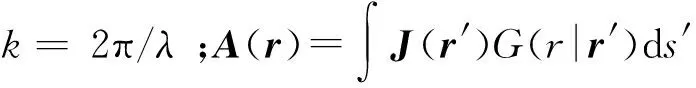
采用RWG矢量基函数将电流展开为

(8)

式中N为MoM基函数数目。则磁流可表示为

(9)

采用伽略金匹配，选用与基函数相同形式的试函数fm作用于式(6)，并将式(7)代入其中得

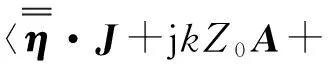
(10)

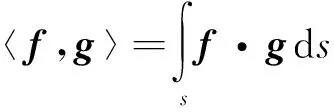
(11)

(12)

将式(12)第一项按泰勒级数展开为

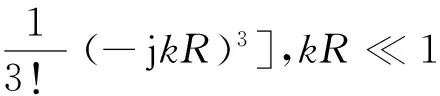
(13)

此项无奇异点，可按常规高斯方法得到数值积分结果。第二项的积分可解析计算得

(14)

(15)

(16)

式中，mi，f3i的表达式见文献[12]。若忽略次要贡献简化后即与文献[13]中的表达式一致。

2 采用多层UV加速MoM

随着目标电尺寸的增大，直接迭代求解MoM矩阵方程带来的N2～3量级的计算量和N2量级的内存需求往往超出计算机的承受能力。为提高各向异性MoM算法的效率，更好地应用于工程实际问题，采用多层UV方法将满秩相互作用矩阵根据电磁相互作用强弱分组，并进行低秩矩阵压缩，加速矩阵元素填充，从而降低内存和计算时间需求。

为了有效甄别出低秩矩阵块，采用类似于快速多级子分层思想，对相互作用矩阵进行分层，以寻求最大化的远区矩阵块。首先用一个几何尺寸略大于目标的立方体(设其边长为l)完全包围目标，作为多层划分的第0层。然后将第0层的立方体等分成8份，得到第1层的8个子立方体。依次递归，直到第L层的子立方体的边长约为0.5λ，将分层后面片索引存入八叉树数据结构。自下而上遍历该八叉树，遍历方法为：直接计算第L层非空结点中基函数的相互作用，得到自作用子块矩阵组及其数目Nself；考察第L层非空结点间的两两相互关系，若结点对应的子立方体相邻(共点、共边或共线)，则计算两结点中基函数的相互作用，得到邻相互作用子块矩阵及其数目Nnear，由于邻相互作用子块矩阵具有一定的低秩性，采用奇异值分解方法处理；考虑第L到第2层各层中非空结点间的两两相互关系，若两结点对应的子立方体在当前层不相邻，而对应的父层结点相邻，则该两结点间为远相互作用，统计远作用组的数目Nfar，远相互作用子块矩阵低秩性十分明显，采用UV分解方法处理。

通过分层，将满秩相互作用矩阵根据电磁相互作用强弱分解成自作用组(强相互作用组)、邻作用组和远作用组(弱相互作用组)三类稀疏子块

(17)

3 数值算例及结果分析

算例1 各向异性阻抗平板。考察边长10 m无限薄正方形平板，各向异性阻抗参数为Zu=2，Zv=5，ξ=35°.平面波入射角θ0=0°～90°，φ0=25°，频率为f=300 MHz，电场θ极化。UV分层数L=4，计算得到的单站RCS结果如图2所示，与文献[6]中提出的各向异性MoM算法的计算结果吻合良好，相应的计算效率见表1.

图2 各向异性阻抗平板的单站RCS

方法未知量耗时/h内存/MBMoM1513064.83511MoM-UV151300.5213

算例2 各向同性阻抗球面。考察入射角θ0=0°，φ0=0°，频率f=300 MHz，电场θ极化的平面波照射直径2a=12 m的球，散射角θ=0°～180°，φ=0°.阻抗参数为Zu=Zv=0.1-j 0.01.考察UV分层数分别为L=3～7的5种情况，计算得到的归一化双站RCS结果如图3所示，与Mie级数结果吻合良好，相应的计算效率见表2.

图3 各向同性阻抗球面的双站RCS

UV分层数未知量耗时/h内存/GB329990113.928.9642999018.356.7352999019.076.5562999019.956.93729990123.657.61

典型算例验证了该各向异性MoM-UV算法的精度，表明效率与传统MoM相比有大幅提升，能在较大程度上增大可求解问题的规模。通过研究发现，与PEC情形相比，相同电尺寸的阻抗面需要划分更多的三角面元才能达到较高的精度，相应的内存及计算时间需求高于PEC情形，凸显出多层UV分解在该三维各向异性阻抗面电磁散射问题求解中的重要作用。通过比较表2中不同UV分层数情形的计算时间和内存需求，说明合理的分层数对该算法计算效率和精度有较大影响。前面已给出分层时的大致原则为递归直到第L层的子立方体的边长约为0.5λ，则分层数L可用包围目标的立方体边长l和雷达波长λ表示，即L≈[log2(2l/λ)]。算例2中分层数为4或5时可使计算效率和精度达到最佳。

4 结 论

基于多层UV矩阵分解技术，提出了用矩量法求解三维各向异性阻抗面电磁散射特性的MoM-UV快速数值算法。UV分解技术相对较新，它不依赖于格林函数的具体形式，只针对远区相互作用矩阵进行低秩压缩，从而加速问题求解。通过若干典型算例，验证了该算法的正确性，从内存耗用和计算时间可以看出，该MoM-UV算法可用于求解较大规模的电磁散射问题。当退化为各向同性或PEC情形时，该算法仍然精确有效，可进行导电面、各向同性以及各向异性阻抗面的快速电磁仿真，为目标的雷达隐身提供理论支持。

[1] 耿友林, 吴信宝, 官伯然. 导体球涂覆各向异性铁氧体介质电磁散射的解析解[J]. 电子与信息学报, 2006, 28(9): 1740-1743.

GENG Youlin, WU Xinbao, GUAN Boran. The analytical solution to the electromagnetic scattering by an anisotropic ferrite-coated conducting sphere[J].Journal of Electronics & Information Technology, 2006, 28(9): 1740-1743.

[2] 陈博韬, 谢拥军, 李晓峰, 等. 各向异性材料部分涂覆导体的散射特性研究[J].电波科学学报, 2009, 24(6): 992-996.

CHEN Botao, XIE Yongjun, LI Xiaofeng, et al. Scattering characteristic of conducting targets with partially-coated anisotropic medium[J].Chinese Journal of Radio Science, 2009, 24(6): 992-996.(in Chinese)

[3] 毛仕春, 吴振森, 邢赞扬. 二维各向异性椭圆柱的电磁散射[J]. 电子学报, 2010, 38(3): 529-533.

MAO Shichun, WU Zhensen, XING Zanyang. Scattering by a homogeneous anisotropic elliptic cylinder: two-dimensional case[J]. Acta Electronica Sinica, 2010, 38(3): 529-533. (in Chinese)

[4] SENIOR T B A, VOLAKIS J L. Approximate Boundary Conditions in Electromagnetics[M]. London: The Institution of Electrical Engineers, 1995.

[5] PELOSI G, MANARA G, FALLAI M. Physical optics expressions for the fields scattered from anisotropic impedance flat plates[J]. Microwave Opt Technol Lett, 1997, 14(6): 316-318.

[6] YU D F, HE S Y, CHEN H T, et al.Research on the electromagnetic scattering of 3D target coated with anisotropic medium using impedance boundary condition [J]. Microwave Opt Technol Lett, 2011, 53(2): 458-462.

[7] TSANG L, LI Q, XU P,et al. Wave scattering with the UV multilevel partitioning method: 2.Three-dimensional problem of nonpenetrable surface scattering [J]. Radio Sci, 2004, 39(5): RS5011.

[8] CHEN H T, ZHU G Q.Using UV technique to accelerate the MM-PO method for three-dimensional radiation and scattering problem[J]. Microwave Opt Technol Lett, 2006, 48(8): 1615-1618.

[9] DENG F S, HE S Y, CHEN H T, et al. Numerical simulation of vector wave scattering from the target and rough surface composite model with 3-D multilevel UV method[J]. IEEE Trans Antennas Propagat, 2010, 58(5): 1625-1634.

[10] RAO S M, WILTON D R, GLISSON A W.Electromagnetic scattering by surfaces of arbitrary shape [J]. IEEE Trans Antennas Propagat, 1982, 30(3): 409-418.

[11] PELOSI G, MANARA G, NEPA P.Electromagnetic scattering by a wedge with anisotropic impedance faces [J]. IEEE Antennas Propagt Mag, 1998, 40(6): 29-35.

[12] GRAGLIA R D. On the numerical integration of the

linear shape functions times the 3-D Green’s function or its gradient on a plane triangle [J]. IEEE Trans Antennas Propagat, 1993, 41(10): 1448-1455.

[13] 盛新庆. 计算电磁学要论[M]. 合肥: 中国科学技术大学出版社, 2008: 23-29.