基于支持向量机的复合柱体目标参数反演
2012-05-29张清河陈将宏
张清河 汪 洋 陈将宏
(三峡大学理学院,湖北 宜昌 443002)
引 言
随着金属/介质复合结构目标(如有耗介质覆盖导体目标、微波传输带、天线-天线罩系统等)的广泛应用,其散射特性的研究近年来得到了很大的关注。自然地,其逆散射方面的研究也就显得十分迫切和重要。目前关于金属/介质复合结构目标电磁逆散射方面的文献报道很少,采用传统的优化迭代方法,一方面由于目标结构的复杂性,其正演的计算较单纯导体或介质目标的计算要复杂一些;另一方面,目标结构的复杂造成逆散射问题的非线性更强,同时,目标函数、优化变量增多,导致迭代很慢或不收敛,严重费时,不利于对目标的实时反演。对于金属/介质复合结构目标电磁逆散射中正演问题的计算,可采用许多比较成熟的算法,如矩量法(MoM)、有限元法(FEM)、时域有限差分法(FDTD)等。在本文中,我们采用基于矩量法的混合体-面积分方程法(VSIE)来求解正散射问题。同时,应用稳定的双共轭梯度结合快速傅里叶变换技术(BCG-FFT)来加速矩阵方程的求解。
近十年,人工神经网络(ANN)技术在电磁逆散射问题研究中得到了广泛的应用[1-5],包括基于频域信息或时域信息、自由空间目标或半空间埋地目标、单纯导体目标或单纯介质目标等。由于神经网络学习方法基于经验风险最小化准则,对于未经训练的新数据,其泛化能力较差,存在过学习、局部最优等问题,使得该方法在逆散射问题中的应用研究停滞不前。最近,一种新的人工智能技术-支持向量机(SVM)被应用到电磁逆散射领域。在文献[6]-[7]中,作者分别以FEM、FDTD作为前向算法,以散射场幅值和相位为训练样本信息,应用SVM在频域研究了半空间埋地目标的逆散射问题,包括埋地目标中心坐标的探测、电磁及几何参数的重构等。SVM是Vapnik等在统计学习理论(SLT)基础上发展起来的一种机器学习算法[8],它不同于神经网络等传统方法以训练误差最小化作为优化目标,而是以训练误差作为优化问题的约束条件,以置信范围值最小化作为优化目标。因此,SVM的泛化能力要明显优越于神经网络等传统学习方法。另外,SVM的求解最后转化成二次规划问题的求解,因此,SVM的解是唯一的、也是全局最优的。正是上述两大优点,使SVM一经提出就得到了广泛的重视。
基于混合体-面电场积分方程,运用BCG-FFT方法作为电磁逆散射问题的前向算法,在此基础上,利用SVM这一人工智能技术研究了金属/介质复合结构目标电磁逆散射问题,实时重构了复合目标的几何、电磁参数。
1 理论分析
1.1 混合体-面积分方程
一金属/介质复合结构目标在入射场Ei照射下,其散射场Es为
Es(r)= -jωAS(r)-ΦS(r)-
jωAV(r)-ΦV(r)
(1)
式中:AS,AV,ΦS,ΦV分别是导体表面感应JS和介质体内极化JV产生的磁矢位和电标位,
(2)

u=S,V
(3)
在介质体内,体电流JV与总场的关系为
(4)
而
Etotal(r)=Ei(r)+Es(r)
(5)
由导体表面边界条件有
(Ei(r)+Es(r))tan=0,r∈S
(6)
将式(5)代入式(4),得到
(7)

(8)

对于矩阵方程(8)的求解,随着计算机技术的发展,一些快速算法获得了广泛的应用,如共轭梯度-快速傅里叶变换方法(CG-FFT)[9]、快速多极子方法(FMM)[10-11]、多层快速多极子方法(MLFMA)[12-13]、自适应积分法(AIM)[14]等。本文采用稳定的双共轭梯度结合快速傅里叶变换(BCG-FFT)方法[15],在BCG迭代过程中,需要大量计算矩阵与向量的乘积,考虑到方程(8)中子矩阵Ztu(u=S,V,t=S,V)分别为二重或三重Toeplitz矩阵,它们与向量的乘积可用FFT加速,只需存储其第一列元素,从而有效地减少计算机内存需求和计算时间,为电磁逆散射问题的求解提供了高效的正演算法。
1.2 回归估计的SVM方法
(9)


(10)
该ε不敏感损失函数被形象地比喻为ε管道,训练的目的是使回归估计函数F(e)与目标值之间的距离小于ε.对所有训练样本,回归估计函数F(e)与目标值之间的距离可表示为
(11)
运用拉格朗日乘子法可将方程(11)的最小化问题转化为一个凸二次规划问题,即[16]
(12)

方程(12)可采用常规的优化技术进行求解,本文采用一种高效的优化算法-顺序优化算法(SMO)[17],减少了SVM的训练时间及计算内存。方程(9)中的参数b可在方程(12)的Karush-Kuhn-Tucker最优化条件(KKT条件)下计算得到[16]。
2 数值结果与分析
2.1 复合目标散射BCG-FFT算法验证
采用BCG-FFT方法计算了两个有意义的二维金属/介质复合结构目标的电磁散射特性,并与FDTD方法作比较,验证本文正散射问题方法的正确性。
2.1.1 不均匀介质覆盖导体圆柱
单位强度TM波沿x轴(设柱体轴线为z轴)入射到无限长不均匀介质覆盖导体圆柱上,导体半径为0.2λ,介质厚度为0.1λ,介质由两种组成,相对介电常数分别为εr1=4.0,εr2=20.0.介质1处于x轴下方,介质2位于x轴上方。图1给出了目标的双站雷达散射截面σ(用波长归一化)。图中还给出了FDTD的计算结果,两者符合得较好,但在200°~250°范围内出现了一定的偏差,一方面可能是由于采用简单的矩形及立方体剖分,另一方面采用中心点匹配,降低了精度。

图1 两种介质覆盖金属圆柱的双站
2.1.2 金属/介质组成复合方柱
单位强度TM波入射到一金属/介质复合方柱目标,入射角φ=270°,目标一半是导体(左边),一半是介质(右边),金属和介质的截面都是边长为0.2λ的正方形,介质的相对介电常数为4.0.图2给出了目标的σ.所得结果与文献[18]的结果一致,图中还给出了FDTD的计算结果。

图2 金属介质复合方柱的双站
2.2 复合目标几何、电磁参数重构
2.2.1 介质覆盖厚度及相对介电常数重构
一单位强度TM平面波(f=1 GHz)垂直照射内、外半径分别为a、b的无耗介质覆盖导体圆柱,a=λ/6.假设b的取值范围为7~23 cm,εr的取值范围为1.5~5.0.在支持向量机的训练阶段,提供了135个训练样本,分别对应目标参数b=7.0+2ncm,n=0,1,…,8及εr=1.5+0.25n,n=0,1,…,14.为了准确而完备地获得目标的散射场,设置了12个散射场观测点,均匀分布在距离目标中心半径为λ、长为3πλ/2的圆弧上,样本信息为观测点散射电场的幅值,可用解析的方法直接得到。经过适当的训练,建立了重构介质覆盖厚度及相对介电常数的SVM逆散射模型,其结构参数分别为(ε,C,σ2)εr=(0.001,999.854 5,0.246 0)及(ε,C,σ2)b=(0.001,1 004.686 7,0.244 1).在测试阶段,测试样本数为96个(不同于训练样本),分别对应目标参数b=8.0+2ncm,n=0,1,…,7及εr=1.55,1.80,2.05,2.30,2.55,2.76,3.05,3.30,3.80,4.50,4.55,4.90.图3(a)、(b)分别给出了复合圆柱目标介质的相对介电常数、覆盖厚度的重构值与实际值的比较示意图,表1是重构值与实际值的误差统计。从表1来看,基于SVM方法的相对介电常数、介质覆盖厚度的重构均获得了较好的结果,其平均相对误差都不超过2%.作为比较,在相同的“条件”下(相同的训练样本、相同的测试样本),还利用ANN方法进行了反演。在该方法中,网络模型为三层BP神经网络(BPNN)[19],网络结构为12-24-2,BP网络训练算法为L-M训练算法,隐含层激活函数为对数型sigmoid函数。图4(a)、(b)分别给出了基于BPNN的相对介电常数、介质覆盖厚度的重构结果,表2是误差统计。

表1 基于SVM的复合圆柱介质相对介电常数、 覆盖厚度反演误差

(a) εr

(b) b图3 基于SVM方法的重构值与实际值

(a) εr
(b) b图4 基于BPNN(12-24-2)方法的重构值与实际值

平均绝对误差最大相对误差平均相对误差εr0.06028.00%2.18%b/cm0.181910.94%1.81%
从表1和表2来看,虽然ANN方法也获得了较好的重构结果,但在相同的训练样本和样本信息条件下,SVM的重构精度要全面优于ANN方法,这也表明了前文所说的SVM的泛化能力要优越于神经网络等传统学习方法。
2.2.2 复合圆柱内、外半径和相对介电常数重构
本算例中要重构的参数为复合圆柱中金属的半径a、介质的半径b及相对介电常数εr,设介质的电导率σ=0.005 S/m.几何模型与上例相同,同样设置12个散射场观测点,样本信息为观测点散射电场的幅值,利用BCG-FFT方法快速得到。总共216个训练样本提供给SVM训练学习,分别对应于目标参数εr=1.5+1.0n,n=0,1,…,5;a=2.0+2.0ncm,n=0,1,…,5及b=14.0+2.0ncm,n=0,1,…,5.经过适当的训练,用于重构复合圆柱内、外半径及相对介电常数的SVM逆散射模型的结构参数分别为(ε,C,σ2)εr=(0.001,999.153 1,0.226 2)、(ε,C,σ2)a=(0.001,999.907 9,0.226 5)及(ε,C,

(a) εr
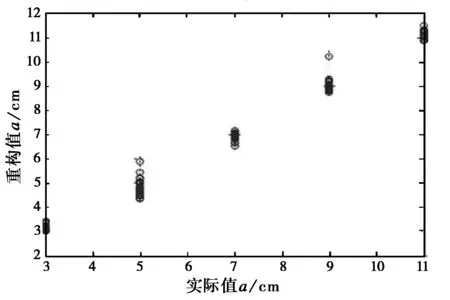
(b) a

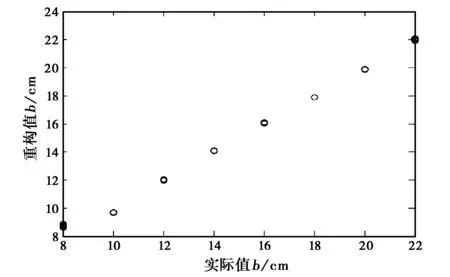
(c) b图5 基于SVM方法的重构值与实际值
σ2)a=(0.01,999.211 1,0.226 2).测试样本数为125个,重构参数的取值范围分别为2.0~6.0、3.0~11.0 cm和15.0~23.0 cm,均不同于训练样本。图5(a)、(b)及(c)分别给出了3个参数的重构值与实际值的比较,表3给出了相应的误差统计。
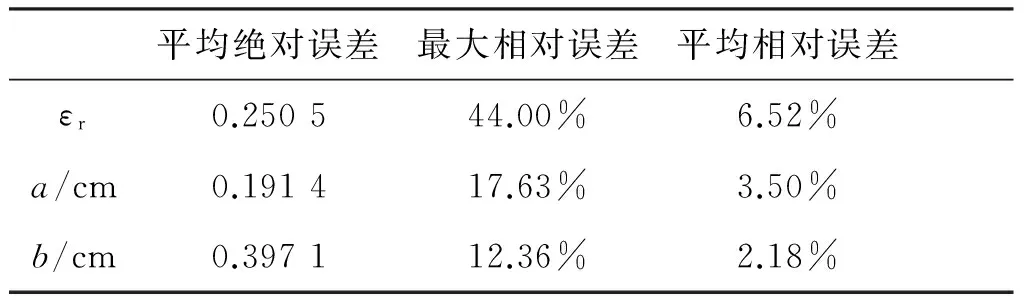
表3 基于SVM的复合圆柱内、外半径以及相对介电常数重构误差统计表
同样地,在相同的条件下,基于BPNN(12-24-3)方法的重构误差见表4.

表4 基于BPNN(12-24-3)的复合圆柱内、外半径以及相对介电常数重构误差统计表
从表3和表4来看,SVM方法要优于BP神经网络,且在对εr重构时,两种方法均产生较大的误差,随着εr值的增大,误差呈增大的趋势,这可以解释为随着εr值的增大,目标愈表现为强散射体的特征。
2.2.3 复合方柱相对介电常数、导体宽度重构
在本算例中,考虑一个二维金属/介质复合方柱目标参数重构问题(见图2)。复合目标一半是导体(左边),一半是介质(右边),目标高度为20 cm,目标宽度为30 cm,其中导体的宽度为a,假设介质是一无耗介质,相对介电常数为εr.与上两例相同,入射波仍为单位强度TM平面波(f=1 GHz),同样设置12个散射场观测点,均匀分布在距离方柱截面中心半径为λ、长为3πλ/2的圆弧上。对于样本信息,我们设计了两种方案,一种是12个观测点散射电场幅值作为样本信息,另一种是把散射电场的幅值和相位作为样本信息。训练样本数240个,分别对应目标参数εr=1.5+0.25n,n=0,1,…,14和a=5.0+1.0ncm,n=0,1,…,15.测试样本数144个,对应的重构参数是εr=1.55,1.80,2.05,2.30,2.55,2.76,3.05,3.30,3.80,4.50,4.55,4.90,a=6.5+1.0ncm,n=0,1,…,11.基于幅值信息的SVM重构误差为:Relerr(εr)max=0.49%,Relerr(εr)ave=0.10%;Relerr(a)max=7.88%,Relerr(a)ave=4.58%.基于幅值和相位信息的SVM重构误差为:Relerr(εr)max=0.48%,Relerr(εr)ave=0.08%;Relerr(a)max=7.85%,Relerr(a)ave=4.58%.其中Relerr()max表示最大相对误差,Relerr()ave表示平均相对误差。
3 结 论
研究了二维金属/介质复合结构目标的电磁逆散射问题。采用BCG-FFT方法快速求解复合结构目标电磁散射正问题,为训练样本的获得提供了高效率的途径。逆问题应用SVM方法,分别重构了复合圆柱、复合方柱目标的几何、电磁参数。从重构的结果和误差分析来看,一般说来,基于SVM的逆散射结果要优于BP神经网络的结果,从而为电磁逆散射研究提供了一种有效的方法。同时,在训练样本较为完备的条件下,对于SVM,适当丰富样本信息并不能明显提高重构的精度。
[1] MYDUR R, MICHALSKI K A. A neural-network approach to the electromagnetic imaging of elliptic conducting cylinders[J]. Microwave Opt Technol Lett, 2001, 28(5): 303-306.
[2] REKANOS I T. On-line inverse scattering of conducting cylinders using radial basis-function neural networks[J]. Microwave Opt Technol Lett, 2001, 28(6): 378-380.
[3] BERMANI E, CAORSI S, RAFFETTO M. An inverse scattering approach based on a neural network technique for the detection of dielectric cylinders buried in a lossy half-space[J]. PIER, 2000, 26(4): 67-87.
[4] BERMANI E, CAORSI S, RAFFETTO M. Microwave detection and dielectric characterization of cylindrical objects from amplitude-only data by means of neural networks[J]. IEEE Trans Antennas Propag, 2002, 50(9): 1309-1314.
[5] BERMANI E, CAORSI S, RAFFETTO M. Geometric and dielectric characterization of buried cylinders by using simple time-domain electromagnetic data and neural networks[J]. Microwave Opt Technol Lett, 2000, 24(1): 24-31.
[6] BERMANI E, BONI A, CAORSI S, et al. An innovation real-time technique for buried object detection[J]. IEEE Trans Geosci Remote Sens, 2003, 41(4): 927-931.
[7] 张清河, 肖柏勋, 朱国强. 基于支持向量机的介质圆柱体逆散射问题研究[J]. 电波科学学报, 2007, 22(2): 234-238.
ZHANG Qinghe, XIAO Boxun, ZHU Guoqiang. Inverse scattering by dielectric circular cylinder based on support vector machine[J]. Chinese Journal of Radio Science, 2007, 22(2): 234-238. (in Chinese)
[8]VAPNIK V. Statistical learning theory[M]. New York: Wiley, 1998.
[9] SARKAR T K, ARVAS E, RAO S M. Application of FFT and conjugate gradient method for the solution of electromagnetic radiation from electrically large and small conducting bodies[J]. IEEE Trans Antennas and Propagation, 1986, 34(5): 635-640.
[10] COIFMAN R, ROKHLIN V and WANDZURA S. The fast multipole method for the wave equation: A pedestrian prescription[J]. IEEE Antennas Propag Mag, 1993, 35(3): 7-12.
[11] 丁振宇, 洪 伟. 快速多极子在任意截面均匀介质柱散射中的应用[J]. 电波科学学报, 2001, 16(3): 283-286.
DING Zhenyu, HONG Wei. Application of FMM to electromagnetic scattering from a homogeneous cylinder of arbitry cross section[J]. Chinese Journal of Radio Science, 2001, 16(3): 283-286. (in Chinese)
[12] SONG J M, LU C C, CHEW W C. Multilevel fast-multipole algorithm for electromagnetic scattering by large complex objects[J]. IEEE Trans Antennas Propag, 1997, 45(10): 1488-1493.
[13] 胡 俊,聂在平,王 军,等.三维电大目标散射求解的多层快速多极子方法[J].电波科学学报,2004,19(5):509-514.
HU Jun, NIE Zaiping, WANG Jun, et al. Multilevel fast multipole algorithm for solving scattering from 3-D electrically large object[J]. Chinese Journal of Radio Science, 2004, 19(5): 509-514. (in Chinese)
[14]BLESZYNSKI E, BLESKYNSKI M, JAROSZEWICZ T. AIM: adaptive integral method for solving large-scale electromagnetic scattering and radiation problems[J]. Radio Sci, 1996, 31(2): 1225-1251.
[15] XU X M, LIU Q H, ZHANG Z Q. The stabilized biconjugate fradient fast fourier transform method for electromagnetic scattering[J]. J Appl Computat Electromagn, 2002, 17(1): 97-103.
[16] CRISTIANINI N, TAYLOR J S. An Introductionto Support Vector Machine[M]. Cambridge: Cambridge University Press, 2000.
[17] PLATT J. Fast Training of Support Vector Machine Using Sequential Minimal Optimization[C]. Cambridge: MIT Press, 1999.
[18] ELSHERBENI A Z, KISHK A A. Modeling of cylindrical objects by circular dielectric and conducting cylinders[J]. IEEE Trans Antennas Propag, 1992, 40(1): 96-99.
[19] 蒋宗礼. 人工神经网络导论[M]. 北京: 高等教育出版社, 2001.
