一类无约束DC规划的全局最优解

李博，卜晴晴

(青岛科技大学 数理学院，山东 青岛 266061)

0 引言

DC规划是非凸规划中的重要内容之一.DC规划又可分为无约束DC规划和约束DC规划[1].本文将对一类无约束DC规划进行研究，寻找这类DC规划的全局最优解.

首先，在本文第一节中给出所要研究的无约束DC规划和一些相关的概念及性质.第二节主要针对该类DC规划，找出它的最优解充分条件、必要条件以及充要条件.

1 基本概念和性质

可以表示成两个凸函数的差的函数称为DC函数.目标函数是DC函数的无约束规划问题称为无约束DC规划.

命题1[2]二阶偏导数处处连续的函数是DC函数.

命题2[3]若f(x)在开凸集S上具有二阶连续偏导数，则f(x)是S上的凸函数的充要条件是：f(x)的海森矩阵▽2f(x)在S上处处半正定.

考虑下面的规划问题：

min{f(x):x∈Rn}

其中f(x)的二阶偏导数处处连续，且▽2f(x)在Rn上处处半正定.

由命题1可知f(x)是DC函数，即f(x)=g(x)-h(x)，其中g(x)，h(x)均为凸函数，因此该规划问题等价于下述无约束DC规划：

min{g(x)-h(x):x∈Rn}

(1)

其中g(x)，h(x)均为凸函数，f(x)=g(x)-h(x)的二阶偏导数处处连续且▽2f(x)在Rn上处处半正定.

下面我们将寻找这类DC规划的最优性条件.

2 最优性条件

定理1 对无约束DC规划(1)，若存在x*，使得▽g(x*)=▽h(x*)，则x*是该规划的局部最优解.

证明因为f(x)=g(x)-h(x)具有二阶连续偏导数，所以对任意的x*∈Rn，f(x)在x*的一个δ邻域N(x*,δ)内二次可微，因此对任意的x∈N(x*,δ)，恒有

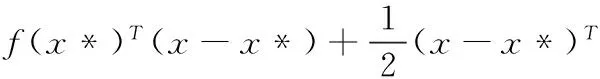
其中0<θ<1.

又因为▽g(x*)=▽h(x*)，故▽f(x*)=0，即▽f(x*)T=0.

因此对任意的x∈N(x*,δ)，恒有f(x)≥f(x*)，即f(x*)是f(x)的局部极小值，所以x*是规划问题(1)的局部最优解.

定理2 对无约束DC规划(1)，若x*是该规划的局部最优解，则有▽g(x*)=▽h(x*).

证明 用反证法.

因为f(x)=g(x)-h(x)二阶偏导数处处连续，所以对任意的x*∈Rn，f(x)在x*处可微.

假设▽g(x*)≠▽h(x*)，则有▽f(x*)=▽g(x*)-▽h(x*)≠0.

令p=-▽f(x*)，则▽f(x*)Tp=-▽f(x*)T▽f(x*)=-||▽f(x*)||2<0.

因为f(x)可微，在x*处对f(x)作一阶泰勒展开，对任意的λ>0，有f(x*+λp)=f(x*)+λ▽f(x*)Tp+ο(||λp||).

因为λ>0，▽f(x*)Tp<0，所以λ▽f(x*)Tp<0.

又因为ο(||λp||)是比||λp||高阶的无穷小量，所以存在δ>0，当λ∈(0,δ)时，恒有λ▽f(x*)Tp+ο(||λp||)<0.

所以对任意的λ∈(0,δ)，恒有f(x*+λp)

这与x*是局部最优解矛盾，因此假设不成立，所以▽g(x*)=▽h(x*).

推论对无约束DC规划(1)，x*是该规划的局部最优解的充要条件是▽g(x*)=▽h(x*).

证明 由定理1和定理2的证明易知该结论成立.

下面考虑该规划问题(1)的全局最优解.

定理3 对无约束DC规划(1)，x*是该规划的全局最优解的充要条件是▽g(x*)=▽h(x*).

证明 由推论可知，x*是该规划的局部最优解的充要条件是▽g(x*)=▽h(x*)，下面只需证明该规划的局部最优解就是全局最优解.

因为x∈Rn，Rn是开凸集，f(x)=g(x)-h(x)的海森矩阵▽2f(x)在Rn上处处半正定，所以由命题2可知g(x)-h(x)是Rn上的凸函数.

由凸函数的性质可知g(x)-h(x)在Rn上的任一极小点就是它在Rn上的全局极小点，即该规划的局部最优解x*是该规划的全局最优解.

所以x*是无约束DC规划(1)的全局最优解的充要条件是▽g(x*)=▽h(x*).

3 小结

本文对一类特殊的DC规划进行研究，利用凸函数的性质，找到了这类DC规划的全局最优解的充要条件.但是这类DC规划仅仅是DC规划中具有较好性质的一个特例，对于一般的DC规划的研究还需要继续进行.

参考文献

[1]杨杰.DC规划的临近点算法和全局收敛性算法[D].南京:南京航空航天大学,2007:1-36.

[2]Horst R, Thoai NV. DC Programming: Overview [J].Journal of Optimization Theory and Applications, 1999,103:1-43.

[3]何坚勇.最优化方法[M].北京:清华大学出版社,2007.

[4]霍斯特.全局优化引论[M].北京:清华大学出版社,2003.

[5]解可新,韩健,林友联.最优化方法[M].天津:天津大学出版社,2008.