基于粗糙集和多元线性回归的电力系统中长期负荷预测

陈 涛，徐学伟，庄雷明，胡向峰，周 超

(临沂供电公司，山东 临沂 276003)

0 引言

电力系统中长期负荷预测是制定电力系统发展计划的基础，也是规划工作的重要组成部分，其目的是为合理安排电源和电网的建设进度提供宏观决策的依据，使电力建设满足国民经济增长和人民生活水平提高的需要［1］。电力负荷受经济、社会等不确定因素影响很大，进行准确地负荷预测是一项复杂的工作，而正确处理相关因素的影响是提高中长期负荷预测精度的关键。

线性回归分析-结果准确、模型解释能力强的特点，因此在电力负荷预测中得到了广泛应用［2］。但采用单一的线性回归模型不能很好地处理影响因素之间的多重相关性、历史数据的模糊性等问题。文献［3-4］采用偏最小二乘回归分析进行负荷预测，较好地克服了影响因素之间的多重相关性的问题；在此基础上，文献［5］根据年度负荷以及主要影响因素的趋势变化特点，采用灰色模型对其进行模拟，以经验风险最小的预测值代替原始数据进行偏最小二乘建模；文献［6-7］从影响因素对负荷影响的不确定性出发，应用模糊线性回归法进行中长期负荷预测；文献［8］提出一种基于带反馈的多元线性回归法的负荷预测模型。上述各方法均在一定程度上改善了预测效果。

粗糙集(rough sets，RS)理论是波兰数学家Z.Pawlak于1982年提出的一种数据分析理论，是研究不精确、不一致、不完整等各种不完备信息的表达、学习、归纳等的方法，其主要思想就是在保持分类能力不变的前提下，通过知识约简，导出问题的决策或分类规则。近年来，RS理论在电力系统中的应用越来越广泛和深入［9-10］。本文采用粗糙集理论，对影响中长期负荷的各种可能因素进行约简分析，得到影响负荷的主要因素，在此基础上，建立多元线性回归模型进行中长期负荷预测。

1 粗糙集理论基本知识

定义2 令R为一族等价关系，对于每个属性子集P，若P∈R，定义一个二元不可分辨关系ind(P)：ind(P)={(x，y)∈U×U|∀a∈P，f(x，a)=f(y，a)}，ind(P)是论域U上的等价关系，关系ind(P)构成U的一个划分，用U|ind(P)表示，其中的任一元素称为等价类。

定义3 令R为一族等价关系，R∈R如果ind(R)=ind(R)-{R}，则称R为R中不必要的；否则称R为R中必要的。如果每一个R∈R都为R中必要的，则称R为独立的；否则称R为依赖的。如果R是独立的，P⊆R，则P也是独立的。设Q⊆P，如果Q是独立的，且ind(P)=ind(Q)，则称Q为P的一个约简。P中所有必要关系组成的集合称为P的核，记作core(P)。

定义4 在信息系统S中，若 P，Q⊆A则 Q的P-正区域posp(Q)定义为

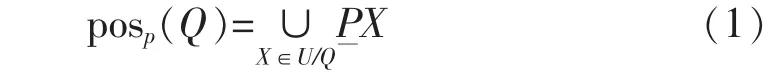
定义5 属性a∈C-R(R⊂C)对于决策属性集 D 的重要度 SGF(a，R，D)定义为

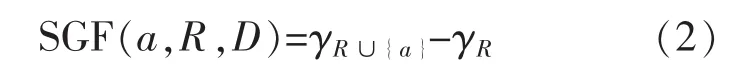
其中，γR=|posR(D)|/|U|

2 基于粗糙集和多元线性回归的负荷预测法

2.1 方法的基本原理

首先采用粗糙集理论的属性约简算法对影响负荷的因素进行约简分析，去除冗余属性，得到影响负荷的决定性因素。然后利用所得的决定性因素建立多元线性回归模型进行负荷预测，方法流程如图1所示。

图1 预测方法流程图

2.2 决策表数据的离散化

运用粗糙集理论时，要求决策表中的属性值为离散值。因此，必须对决策表中的连续属性值进行离散化，即把连续属性的取值范围或取值区间划分为若干个数目不太多的小区间，其中每个小区间对应着一个离散的符号。本文采用等距离离散化方法进行数据离散化处理［12］。

1)计算属性的区间长度

2)确定属性的区间范围

对于第i个属性的各区间的范围为

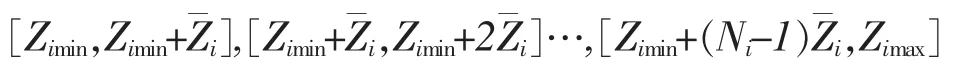
3)计算属性的量化值

每个属性共有Ni个区间，对于一个属性中的值，如果它位于第 n(n=1，2，...，Ni)个区间，则其值为n。

2.3 决策表的属性约简

决策表的简化就是简化决策表的属性，属性约简是指在保持信息系统的分类或决策能力不变的条件下，删除其中的冗余属性。求所有的约简或相对约简已被证明是NP完全问题，故一般采用启发式信息找出最优或次优约简。但很多算法都是不完备的，不能保证一定能得到约简。本文采用文献［13］提出的一种完备的属性约简算法对影响负荷的因素进行约简。

1)计算C相对于D的核coreD(C)；

2)RED=coreD(C)(RED为C相对于D的某个约简)；

3)计算 pocC(D)，U/RED 和 posRED(D)；

4)若|posC(D)|≠posRED(D)，反复执行：

在 C-RED 中找出使 SGF(a，RED，D)取最大值的属性a；

将a加入到RED的尾部，计算新的U|RED和posRED(D)。

5)从RED的尾部开始，从后往前对每个属性a进行判断是否可省：

若a∈coreD(C)，则从a开始往前的属性都是不可省的，算法结束，RED就是所求结果：否则，若 |posC(D)|=|posRED-{a}(D)|，则说明 a 是可省的，从RED中把a删除。

需要说明的是，本文只列出了属性约简算法的关键步骤，具体细节请参考文献［13］。

2.4 多元线性回归模型的建立

多元线性回归模型为

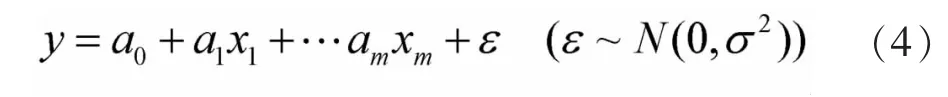
式中：a0，a1，...am为回归系数；ε 是随机误差。

在负荷预测中，将历史数据代入式(4)可得

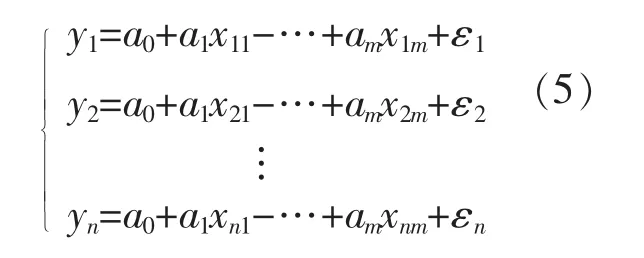
采用最小二乘法求未知参数a0，a1，…，am的估计量，代入式(4)得回归方程

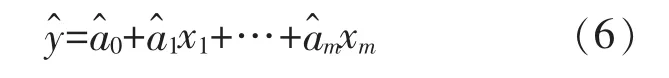
为进一步分析回归模型所反映的变量之间的关系是否符合客观实际，引入的影响因素是否有效，需要对回归模型进行检验。常用的检验方法有；

1)R检验法。通过复相关系数R检验自变量与因变量之间的线性相关程度。若R较大，则多元回归模型的线性近似程度较高；若R较小，则多元回归模型的线性近似程度较低。

2)F检验法。通过F统计量检验自变量与因变量之间回归效果的显著性。若回归效果不显著，则该回归模型就不能用来预测，需分析其原因另选自变量或改变预测模型的形式。

3 算例分析

3.1 基本资料

本文采用文献［3］中的算例，该算例收集了四川省1978-1996年年用电量及其影响因素的资料，见表1。表中电量单位为“亿kWh”，人口单位为“万人”，产业值单位为“亿元”。影响年用电量的因素有国民生产总值x1，第一产业生产值x2，第二产业生产值x3，第三产业生产值x4和总人口x5。用1978-1993年资料建模，1994-1996年资料进行检验。

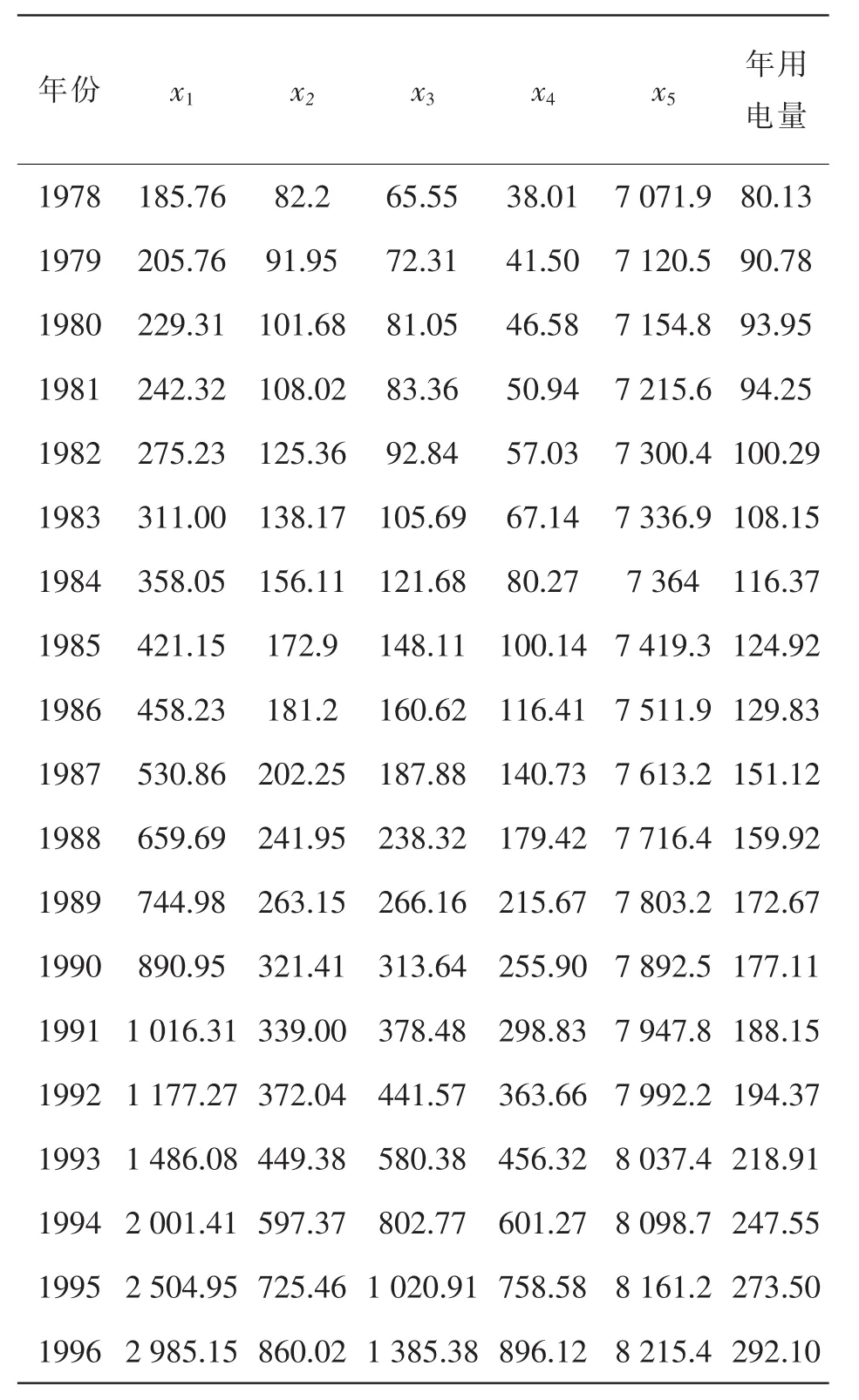
表1 四川省年用电量及其影响因子的基本资料

3.2 属性的离散化

为了减少数据尺度对分析结果的影响，从表1中生成1979-1993年各属性的增量，作为分析负荷与影响因素之间关系的基础数据，如表2所示。

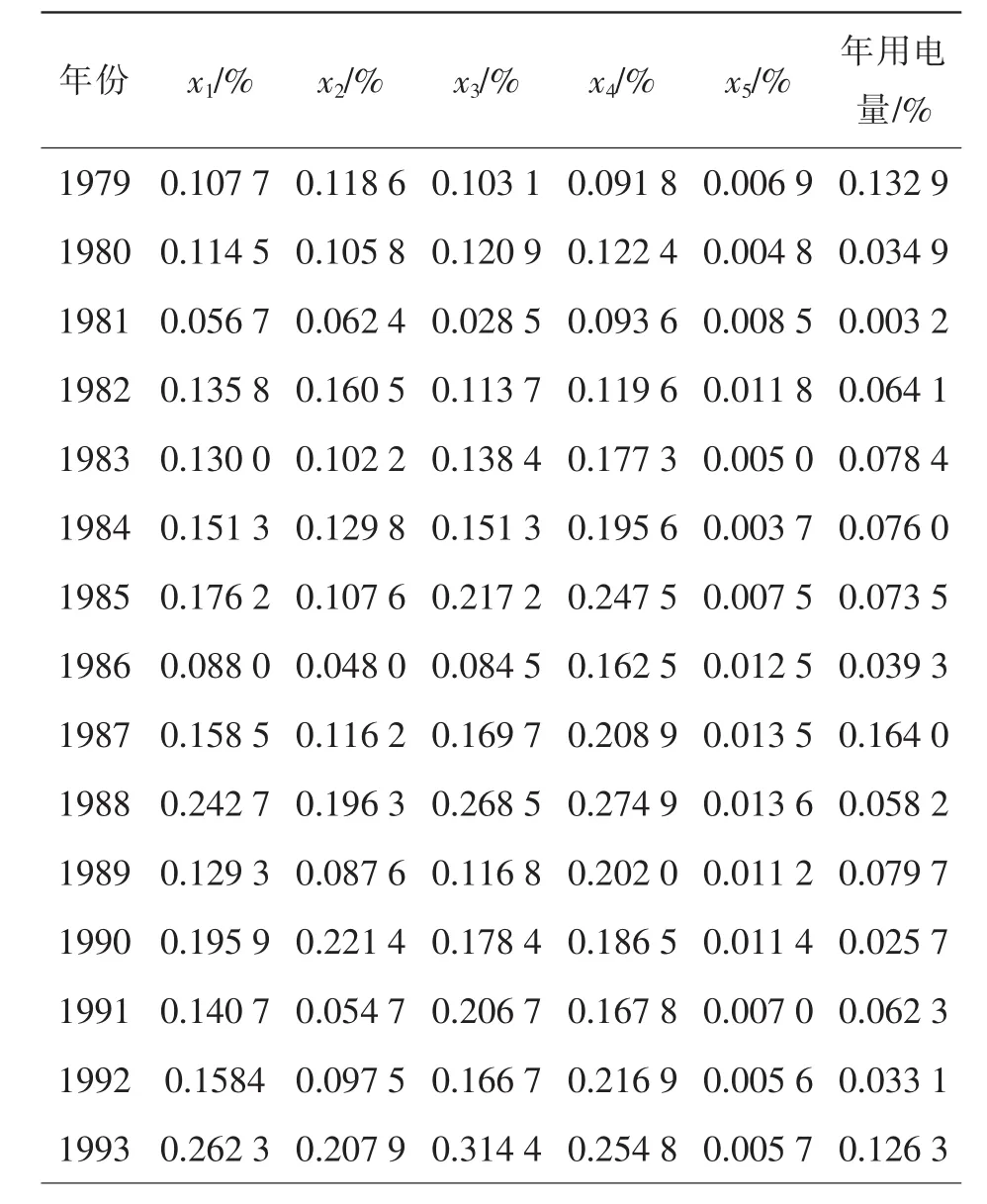
表2 用年增长率表示的负荷及影响因素数据(1979-1993)

将每个条件属性和决策属性均分为4个等级，利用式(3)确定离散各属性区间，根据各属性区间大小对数据进行离散，结果如表3所示。

表3 离散化的决策表

3.3 属性约简

在进行属性约简时，调用文献［14-15］利用MATLAB编写的粗糙集数据分析工具箱(rough set data analysis，rsda)中的函数 redu 实现，该函数采用的约简算法为文献［12］提出的算法。函数的调用格式为 y=redu(c，d，S)。 其中，信息系统决策表由矩阵S表示，向量c和d分别为条件属性C和决策属性D的编号。

属性约简结果表明国民生产总值，第二产业生产值，第三产业生产值和总人口这4个因素是不能约简掉的，而第一产业对负荷影响并不大。

3.4 负荷预测

利用1978—1993年的国民生产总值，第二产业生产值，第三产业生产值、总人口和负荷的历史数据建立多元线性回归模型，采用最小二乘法进行参数辨识，可得

以上结果置信度95%，且R2=0.993，说明有99.3%的影响因素可以由此模型来解释，表明所建立的回归模型较好。可以查出，当α=0.05时，γα=0.497 3，|R|=0.996 5＞0.497 3。 并且 F=387.433 1，说明回归方程的回归效果显著。

利用式(7)及表1中的数据对1994—1996年的用电量进行预测，结果如表4所示。并将本文方法与文献［3］采用的偏最小二乘回归法的预测效果进行对比。两种方法预测结果的平均绝对百分比误差(MAPE)如图2所示。由表4和图2可以看出，本文提出的中长期负荷预测法的预测效果优于偏最小二乘回归法。

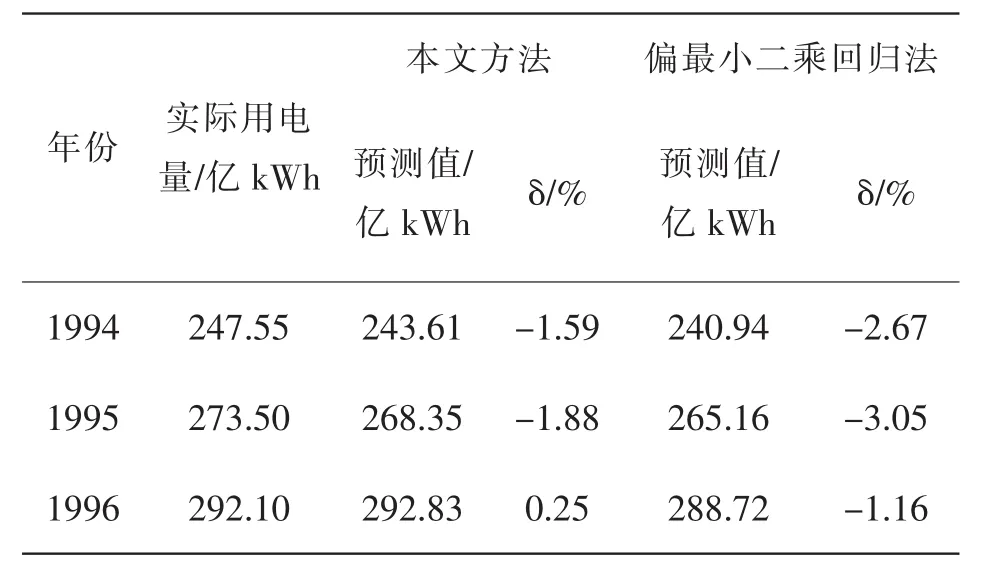
表4 预测结果比较

4 结语

粗糙集完全从历史数据中发掘信息，不需要除数据之外的任何先验知识，可以有效地从影响负荷的众多相关因素中优选出相关度最高的因素，适用于中长期负荷预测。

图2 预测方法的平均绝对百分比误差比较

采用了一种高效、完备的属性约简算法对影响负荷的因素进行属性约简。

利用多元线性回归建立预测模型，具有有模型简单、预测结果准确、模型解释能力强的特点。

实际电力系统负荷预测算例表明所提方法可以有效地提高负荷预测精度，具有一定的实用性。