修理工可单重休假且延迟修理的预防维修更换策略
2012-05-22李海霞孟宪云陈雁东蒋燕美陈变娟
李海霞, 孟宪云, 陈雁东, 蒋燕美, 赵 丹, 陈变娟
(1.燕山大学 理学院 河北 秦皇岛 066004;2.山西省广灵县第一中学校 山西 大同 037500)
0 引言
可修系统的最优更换问题已经成为该领域研究的热点,基于“修复如新”的系统,许多学者经过研究并取得了不少成果[1-2].文献[3]针对系统修理后的寿命随机递减、维修时间随机递增而最终系统不能再工作也不能再修理的问题,提出了“几何过程”.文献[4-5]对预防维修能够“修复如新”,而故障维修为“修复非新”的系统进行了讨论.文献[6]对有延迟修理的修理工多重休假的单部件可修系统进行了讨论.文献[7]对单重休假的可修系统进行了讨论.文献[8-9]对预防性维修策略进行了讨论.
本文假定系统预防维修为“修复如新”,而故障维修为“修复非新”,且系统每次故障以概率1-p延迟修理,并选择以系统的故障次数N为更换策略,利用更新过程和几何过程理论,使得系统经长期运行单位时间内期望费用达到最小.另外,对预防维修的定长间隔时间T及更换策略N也进行了讨论.最后,通过数值算例分析了该结果的有效性.
1 模型假设
假设1设t=0时,系统是新的,修理工开始一次休假,且假定休假时间小于预防维修的定长间隔时间T.休假结束时,若系统的工作时间达到指定时间T尚未发生故障,修理工立即对系统进行预防维修,且假定预防维修是“修复如新”的;若系统故障,修理工对其进行修理;若系统没有故障,修理工等待,待系统的工作时间未达到指定时间T而发生故障时,修理工对其进行修理,且假定故障维修是“修复非新”的,预防维修和修理结束,开始下一次休假.
假设4系统更换时,用新的同型部件更换,更换如新,且更换时间忽略不计.
假设5系统在单位时间内的工作报酬、故障维修费用、预防维修费用、待修时造成的损失和故障后延迟修理造成的损失分别为C1,C2,C3,C4,C5,而系统更换一次费用为C.
2 主要结果及证明
定理1系统的故障次数为N时,系统经长期运行单位时间内期望费用为
(1)
其中,
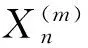
图1为系统的一个可能进程图,设τ1为系统第一次更换时间,τn(n≥2)为系统第n-1次更换与第n次更换之间的间隔时间.显然,{τ1,τ2,…}为一个更新过程,相邻两次更换的间隔时间为一个更新周期.令D(N)为系统经长期运行单位时间内期望费用,根据更新报酬定理得
(2)

图1 系统的一个可能进程图Fig.1 A possible progressive figure of the system
由系统进程图1以及模型假设得更新周期长度为
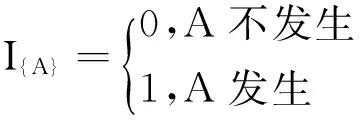
根据文献[4]中定理1及条件期望的性质知,
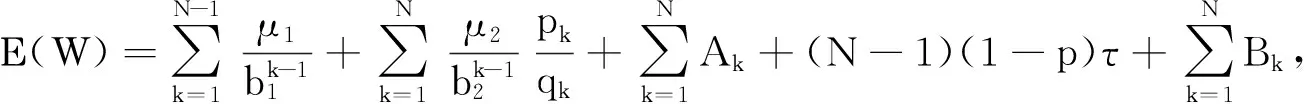
(3)
(4)
将(3)式和(4)式代入(2)式得定理.证毕.
推论在本文考虑的策略中,如不考虑预防维修,则公式(1)中的结果DN为
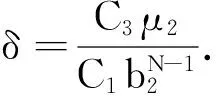
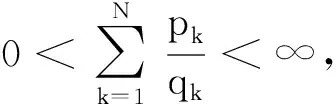
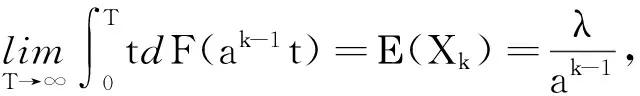
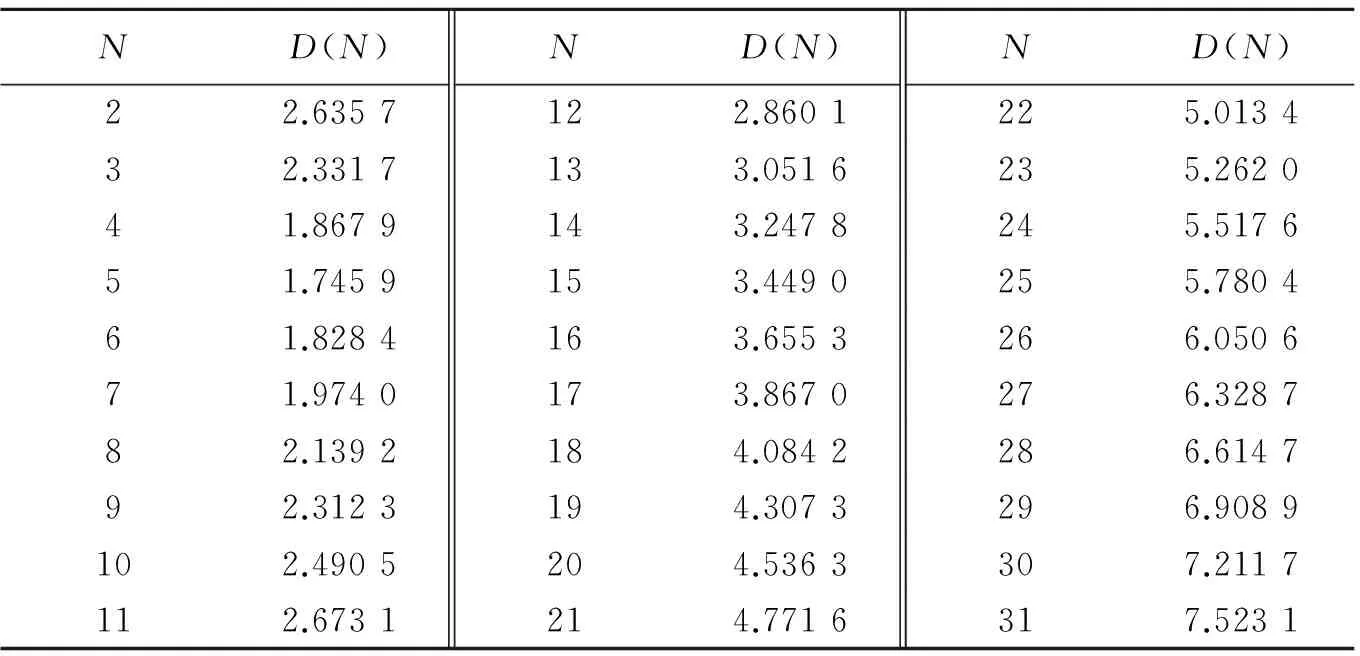
因为B(T,N)为关于T的单调减函数,所以C(N)为其下确界,如果D(N)≥C(N),则有C(N)≤D(N) 由定理2可得 因此本文的策略N*优于C(N)中的策略N**. 设Xn,Yn,Zn,Wn及Vn的分布函数分别为 其中,a>1,0 (5) (6) (7) 将(5),(6)和(7)式代入(1)式,则(1)式成为 (8) 其中, 令a=1.01;b1=0.95;b2=0.98;d=2;λ=600;μ1=16;μ2=8;β=400;τ=0.6;C1=15;C2=45;C3=30;C4=22;C5=25;C=10 000;T=720;p=0.7,由(8)式得表1. 由表1可知,系统经长期运行单位时间内最小期望费用为Dmin(5)=1.745 9,即最优的更换策略为N*=5,且是唯一存在的. 表1 D(N)随N的变化规律Tab.1 The change of D(N) over N 本文提出了一类新的修理工单重休假且延迟修理的预防维修更换模型.该模型以系统的故障次数为更换策略,选取系统经长期运行单位时间内期望费用为目标函数,利用几何过程和更新过程的理论,建立了数学模型,并通过数值算例验证了该结果的有效性.特别地,本文的策略N优于不考虑预防维修的策略N.该结果对指导企业合理使用及维护设备、降低生产成本、提高经济效益和系统安全性都具有一定的指导意义和参考价值. 参考文献: [1] Liu X G, Makis V, Jardine A K S. A replacement model with overhauls and repairs[J]. Naval Research Logistics, 1995,42(7):1063-1079. [2] Wang H, Pham H. A quasi renewal process and its applications in imperfect maintenance[J]. International Journal of Systems Science, 1996,27(10):1055-1062. [3] Lam Y. Geometric processes and replacement problem[J]. Acta Math Appl Sinica, 1988,4(4):366-377. [4] 贾积身,张元林.计及预防维修时间的一个故障维修模型[J].高校应用数学学报, 1997,12(4): 425-432. [5] 贾积身.不计预防维修时间的一个最优更换策略[J].河南师范大学学报:自然科学版, 1997,25(3):10-13. [6] 贾积身,刘思峰,党耀国.延迟修理的修理工多重休假可修系统更换模型[J].系统工程与电子技术, 2009,31(12):3017-3021. [7] 贾鹏茹,孟宪云,张晓爽,等.修理工单重休假的可修系统的更换策略[C]//中国运筹学会第十届学术交流会.北京, 2010:244-249. [8] Zhang Yuanlin. A geometric process repair-model with good-as-new preventive repair[J]. IEEE Transactions on Reliability, 2002,51(2):223-228. [9] Wang Guanjun, Zhang Yuanlin. Optimal periodic preventive repair and replacement policy assuming geometric process repair[J]. IEEE Transactions on Reliability, 2006,55(1):118-122.3 数值算例
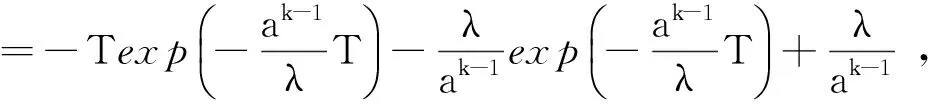
4 结论
