工件有工期并且可拒绝单机最小化最大提前时间的排序问题
2012-05-22聂玲,程涛
聂 玲, 程 涛
(1.郑州大学 数学系 河南 郑州 450001; 2.河南工业大学 理学院 河南 郑州 450001)
0 引 言
排序问题是一类重要的组合最优化问题, 它广泛应用于管理科学、计算机科学、工农业生产和交通运输等许多领域, 一直受到国内外学术界的重视.
在经典排序问题中,总是要求每个工件必须被加工,并且其加工时间是预先给定不变的.然而,在现实生活中, 由于某些外在的因素,需要拒绝加工某些工件才能满足限定条件,这就是可拒绝排序[1-5].当然,拒绝加工一个工件需要付出一定的代价,称之为拒绝费用.本文的研究工作就是设计一种策略或算法,在原始的某个和时间有关的目标函数(最大完工时间、总完工时间、最大提前时间等) 与拒绝费用之间达到一种协调,以取得某种意义下的最优.

1 问题1|nmit|Emax
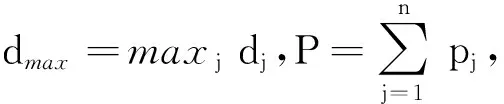
定理1对于排序问题1|nmit|Emax,STST规则得到的是最优排序.
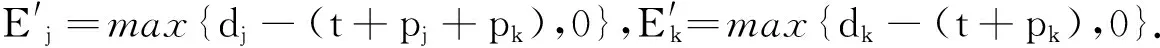
由定理1可知,按照STST规则所得的排序是最优的,并且它的运行时间为O(n2logn).
2 问题

对于排序问题1nmitEmax,已经证明存在一个最优排序,使得工件按照STST规则在机器上加工.因此,有引理1.
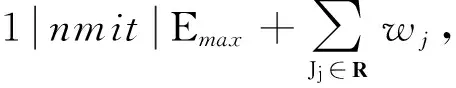
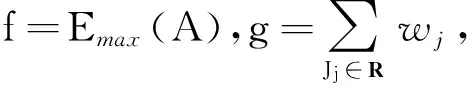
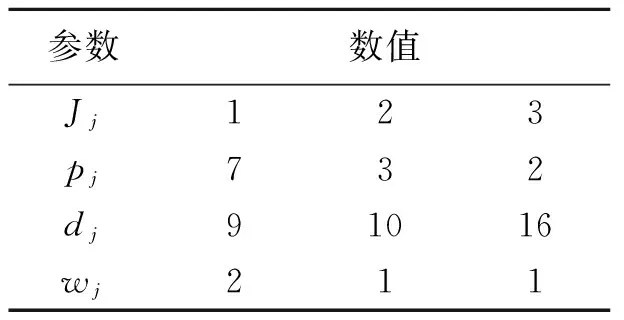
定义1设σ为性能指标为f和g的双指标排序问题的一个可行排序,若不存在可行排序π使得f(π) 定义2由所有Pareto最优点构成的点集所生成的凸包的下沿界称为有效边界;有效边界上的点称为极点;极点对应的排序称为极序. 一般地,只要确定有效边界,则可求出目标函数αf+βg(α和β给定)的最小值.而此时,有效边界为分段线性的凸函数,其中每一个折点对应某一个Pareto最优点,即所有的Pareto最优点或者恰位于有效边界上,或者高于此有效边界. 定理3设T={Jj∶Ej=E*},则要使E*变小,只能通过删去T中的所有工件,并且T={Jk,Jk+1,…,Jl},其中Jk,Jk+1,…,Jl为被接收工件集A中按照STST序最后加工的工件. 证明由引理1,可知被接收工件只有按照STST序加工,才能得到Emax(A)的最小值,即更序无效. 表1 工件参数表Tab.1 The parameter of jobs 表2 计算结果Tab.2 The results of calculations 算法1 Step1:令A∶=N,R∶=∅; 算法2: Step1:令A∶=N,R∶=∅; Step2:计算Emax(A)=maxJj∈A{Ej}; Step3:记T={Jk∶Ek=Emax,Jk∈A}; Step4:令A′∶=AT,计算Emax(A′); 本文首次考虑了目标函数为极小化最大提前时间加上被拒绝工件的拒绝费用之和的工件可拒绝的单机排序问题. 通过对此问题的Pareto最优点的分析, 得到多项式时间可解的算法. 参考文献: [1] Brucker P,Gladky A,Hoogeveen H,et al. Scheduling a batching machine[J].Journal of Scheduling,1998,1(1): 31-54. [2] Bartal Y,Leonardi S,Spaccamela A M,et al. Multiprocessor scheduling with rejection[J]. SIAM Journal on Discrete Mathematics,2000,13(1): 64-78. [3] Engels D W,Karger D R,Kolliopoulos S G, et al. Techniques for scheduling with rejection[J]. Journal of Algorithms, 2003, 49(1):175-191. [4] Hoogeveen H. Multicriteria scheduling[J]. European Journal of Operational Research,2005,167(3): 592-623. [5] Hoogeveen J A,van de Velde S L.Scheduling with target start times[J].European Journal of Operational Research,2001, 129(1): 87-94. [6] Graham R L, Lawer E L, Lenstra J K, et al. Optimization and approximation in deterministic sequencing and scheduling: a survey[J]. Annals of Discrete Mathematics, 1979,5: 1-15. [7] 任立莉,李娅,李阳,工件可拒绝平行机排序[J].郑州大学学报:理学版,2010,42(3):15-18.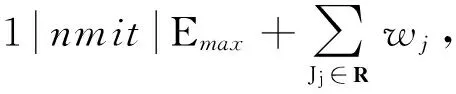

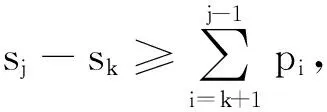

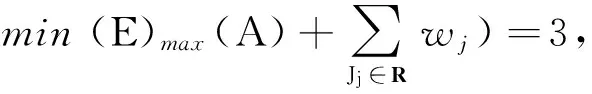
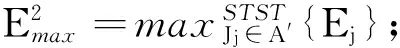
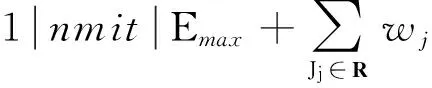
3 总结
