重复模糊简约合作对策核心的特征

徐 刚， 于泳波

(1.东北石油大学秦皇岛分校 基础部 河北 秦皇岛 066004；2.秦皇岛兴荣海事中等职业学校 基础部 河北 秦皇岛 066100)

0 引言

1944年Von Neuman和Morgenstern建立对策论以来，合作对策得到了广泛的研究.1965年Davis和Mascher[1]提出了简约对策，1974年Aubin[2]等人将模糊理论和对策理论结合起来进行研究，1990年Kalai[3]对重复非合作对策进行了深入的研究，1999年Jorge[4]首次提出了重复合作对策的核心，而在2007年Hwang[5]提出了模糊简约模型并进行了分析.本文运用Jorge oriedo处理重复合作对策的方法，将Hwang引入的模糊简约对策加入了重复对策理论，建立了重复模糊简约对策并研究了其核心的公理化特征.

1 基本概念

N={1,2,…,n}是非空的局中人集合，模糊结盟α∈[0,1]N，αi称为局中人i在模糊结盟α的参加率.总结盟eN=(1,1,…,1)；空结盟e∅=(0,0,…,0)；常义结盟S∈2N；类常义结盟eS,S∈2N.这里eS∈FN，若i∈S则(eS)i=1；若i∈N/S,则(eS)i=0.带局中人N的模糊合作对策用FGN表示.记Car(α)={i∈N:αi>0}为S的支集.

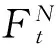
定义2用αt⊆[0,1]N表示第t次对策形成的一个模糊结盟，假设对策从t=0开始，对于t≥0,令(α0,α1,…,αt)依次表示从0到t形成的模糊结盟序列，并且令Ht=(2N)t为到第t阶段所有结盟序列空间，其中2N是N的子集集合，H是模糊结盟序列集合.Nm表示每次均为N形成的结盟序列.

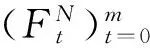
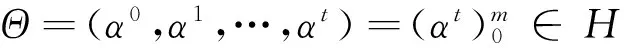
令(H,W)是重复模糊合作对策，(H,W)的支付序列X∶H→R，则

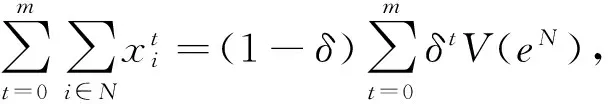
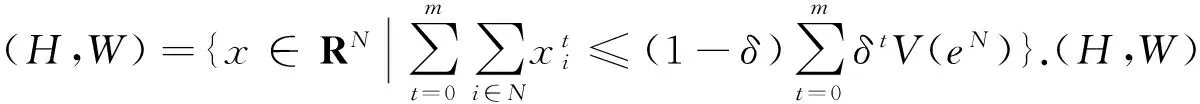
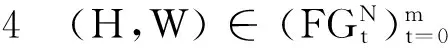
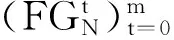
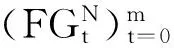
(i)σ满足有效性(Eff),若σ(H,W)⊆X(H,W);

(ii)σ满足个体合理性(Ir),若σ(H,W)⊆I(H,W);

(iii)σ满足单人合理性(Opr),若N=1，σ(H,W)=I(H,W).

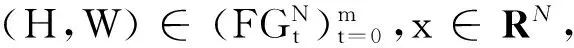
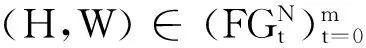
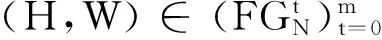
2 基本原理

下面运用Opr，Ir，CON和WCCON来刻画重复模糊简约对策核心的特征.

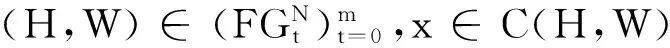
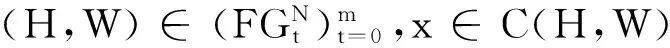
定理1重复模糊对策的核心满足连续性.

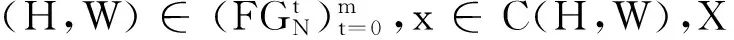
定理2重复模糊对策的核心满足弱反连续性.

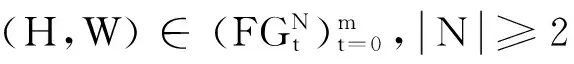
情形1N=2，假设N={i,j}.

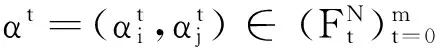
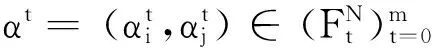
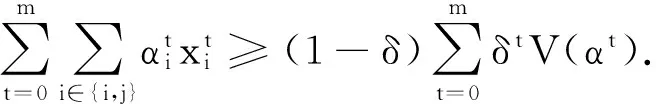
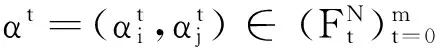
情形2N>2.

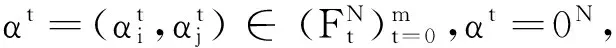
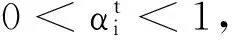
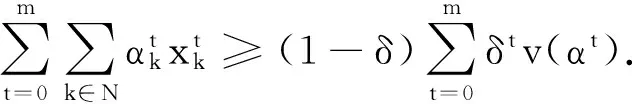
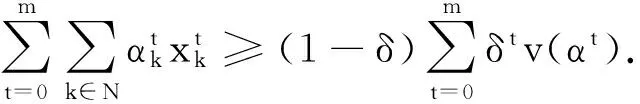
定理3令σ是重复模糊对策的解，若σ满足Opr和CON，则σ也满足Eff.

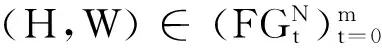
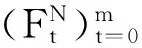
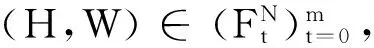
参考文献：

[1] Davis M, Maschler M. The kernel of a cooperative game[J].Naval Research Quarterly,1965,12(3): 223-259.

[2] Aubin J P. Coeur et valeur des jeux flous a paiements lateraux[J].C R Acad Sci Paris:A, 1974, 279:891-894.

[3] Kalai E. Bounded rationality and strategic complexity in repeated games[C]//Sandiego CA:Academic Press,1990:131-157.

[4] Oviedo J. The core of a repeatedn-person cooperative game[J].European Journal of Operational Research, 2000,127(3):519-524.

[5] Hwang Y A. Fuzzy games: a characterization of the core[J]. Fuzzy Sets and Systems, 2007,158(22): 2480-2493.