具有双向耦合的混沌系统的完全同步

付士慧， 魏红军， 刘 洋

(郑州大学 数学系 河南 郑州 450001)

0 引言

非线性系统中的混沌控制与同步是当今非线性科学中一个富有挑战性和具有应用前景的课题.同步在自然界中经常存在，在通信、控制、机械、电路和生物系统特别是保密通讯都有着重要的应用. 有些同步是有益的，如调和振子的生成、保密通讯及组织管理的协调等，我们需要这种同步；有些同步是有害的，如传输控制协议窗口的增加，因特网或通讯网络中信息拥塞等，我们要尽量避免这种同步.到目前为止，人们已经对多种同步类型(完全同步[1]，滞后同步[2]，期望同步[3],预测同步[1]，广义同步[1]等等)和实现同步的多种方法(驱动-响应同步法，自适应同步法[4]，脉冲同步法[5]，观测器同步法[6]等)进行了研究，并且取得了丰富的成果.

完全同步是最简单的混沌同步类型，对它的研究，无论在理论上还是在方法上都较其他的同步类型完善.对于混沌系统的完全同步，耦合方式主要有两种：单向耦合和双向耦合.被耦合的系统之一并不会随着耦合而发生变化，这种耦合称为单向耦合；相反的两个系统之间相互影响，则这种耦合称为双向耦合[1].Hebertt[7]对单向耦合的混沌系统通过广义哈密顿系统和观测器的方法研究了其同步问题，这种方法还被推广到时滞系统，对保密通信中的应用进行了研究[8].Mu等[9]利用该方法还研究了变参数混沌系统的同步问题.本文将该方法进一步推广到了双向耦合的混沌系统.

1 双向耦合系统的完全同步

给定光滑系统

(1)

其中f∈Rn是连续可微的.

通过广义哈密顿系统，方程(1)重新被表示

(2)

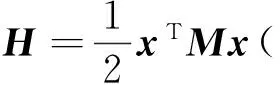
利用观测器法，构造驱动系统和响应系统分别为

(3)

和

(4)

其中y是系统的输出量，矩阵C是常数矩阵；ξ和η分别为x和y的扰动；K,K1是常数矩阵.

接下来的主要工作是设计K,K1，使驱动系统(3)及其相应的响应系统(4)能够达到完全同步.

记

e(t)=x(t)-ξ(t),ey=y-η，

则方程(3)和(4)的误差系统为

(5)

要使系统(3)和(4)能达到完全同步，只需误差系统(5)的零解是稳定的.为此，下面的定理1主要给出了当K,K1满足一些条件时系统(5)的零解是稳定的.

定理1若矩阵

是负定的，则误差系统(5)的零解是稳定的，即驱动系统(3)和其相应的响应系统(4)能够达到完全同步.

证明令Lyapunov函数v=H(e)则

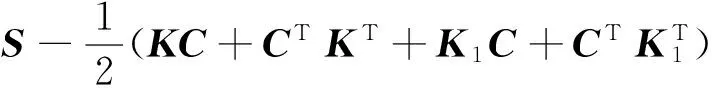
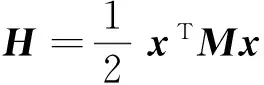
2 数值仿真

洛伦兹系统的动力学方程为

(6)

根据方程(2)，重新设计系统(6)得

(7)

其中

根据方程(3)和(4)，则驱动系统和响应系统分别为

(8)

和

(9)

其中

因此误差系统为

(10)

即

(11)

由上述定理，据Sylvester准则，当满足

k1+K1>-σ,σ(1-K2-k2)2<4(σ+K1+k1)

时，误差系统(11)的零解是稳定的，这也表明驱动系统(8)及其响应系统(9)达到了完全同步.

取定参数

系统(8)和(9)的相位图如图1和图2所示，从图中可见系统的运动是混沌的；其相应的误差系统(11)随时间变化的历程图如图3～5所示，状态变量很快趋于零，这说明系统(8)及其相应的系统(9)很快达到了完全同步.同步速度与参数的选取有一定的关系，若参数选取在同步条件的边界附近，同步速度可能相对慢些.

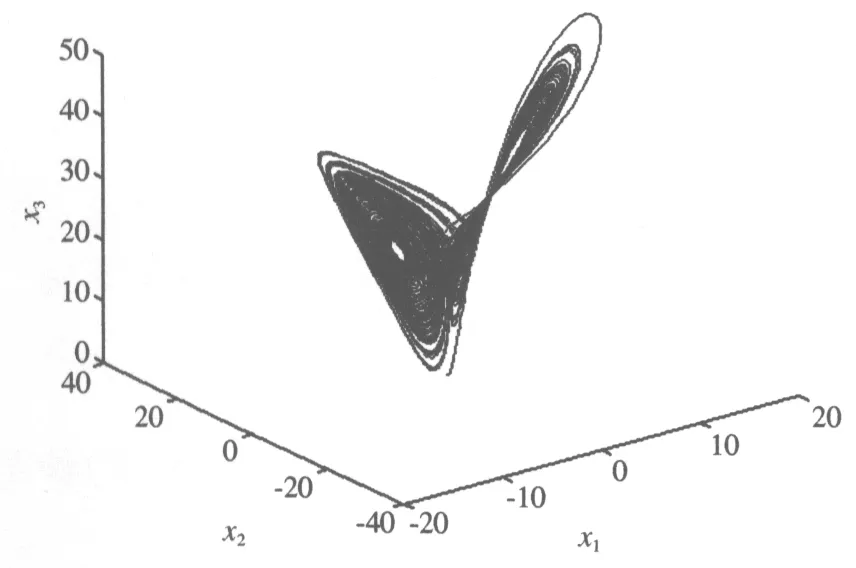
图1 系统(8)的相位图 Fig.1 Phase diagram of equation (8)

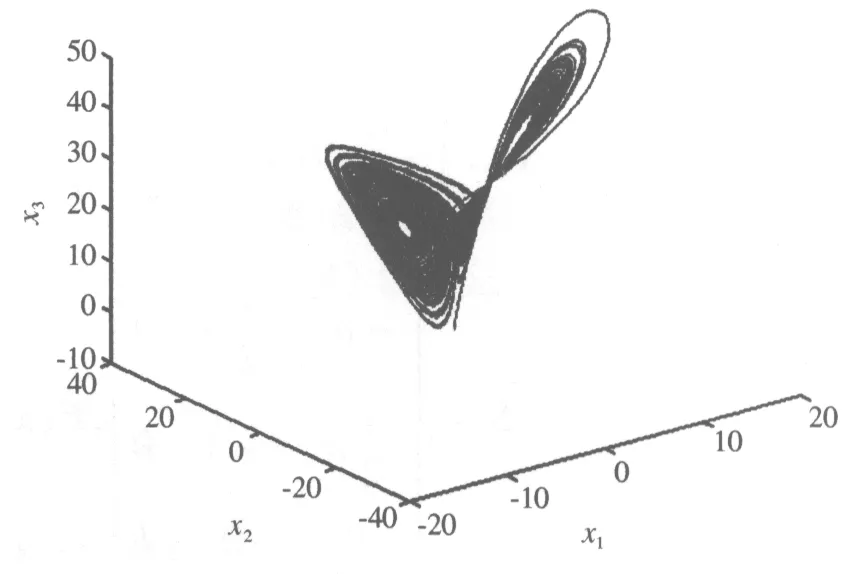
图2 系统(9)的相位图Fig.2 Phase diagram of equation (9)

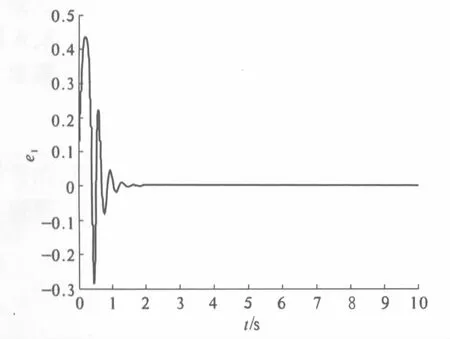
图3 误差系统(11)的时间历程图 Fig.3 Time history of e1 in error system (11)

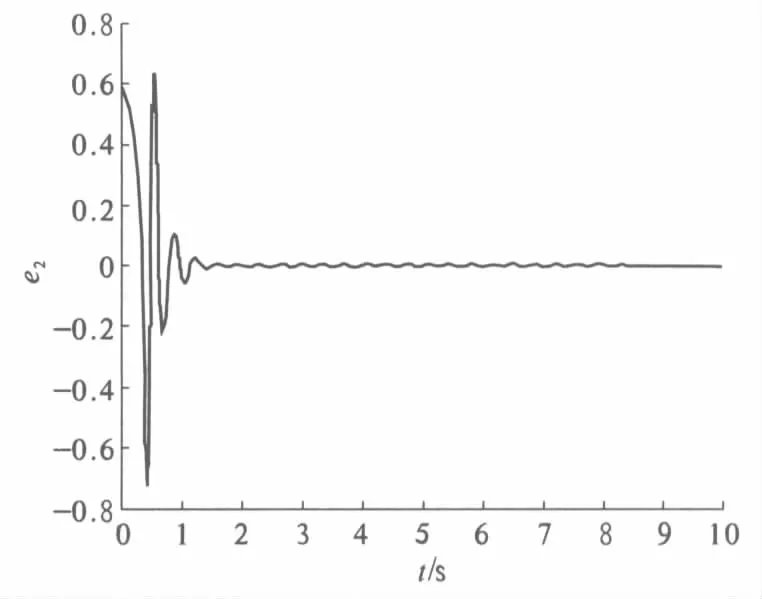
图4 误差系统(11)的时间历程图Fig.4 Time history of e2 in error system (11)

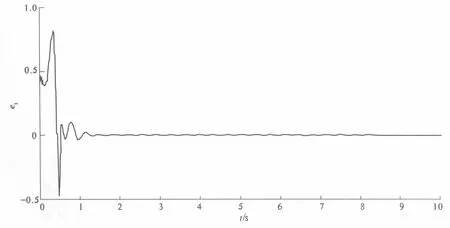
图5 误差系统(11)e3的时间历程图Fig.5 Time history of e3 in error system (11)

3 结论

通过广义哈密顿系统和观测器方法对混沌系统重新设计后，构造了具有双向耦合的驱动和响应系统；利用Lyapunov稳定性理论研究了误差系统零解的稳定性，给出了完全同步的条件；数值结果也表明了该方法的正确性.

参考文献：

[1] Boccaletti S, Kurths J, Osipov G, et al. The synchronization of chaotic systems[J]. Physics Reports, 2002, 366: 1-101.

[2] Shu Y L, Zhang A B, Tang B D. Switching among three different kinds of synchronization for delay chaotic systems[J]. Chaos, Solitons & Fractals, 2005, 23(2): 563-571.

[3] Senthilkumar D V, Lakshmanan M. Transition from anticipatory to lag synchronization via complete synchronization in time-delay systems[J]. Phys Rev E, 2005, 71: 016211.

[4] 王兴元，武相军. 耦合发电机系统的自适应控制与同步[J]. 物理学报，2006, 55(10): 5077-5082.

[5] 陈菊芳，张入元，彭建华. 脉冲驱动离散混沌系统同步的实验与理论研究[J]. 物理学报，2003, 52(7): 1589-1594.

[6] 关新平，何宴辉，范正平. 扰动情况下一类混沌系统的观测器同步[J]. 物理学报，2003, 52(2): 276-280.

[7] Sira-Ramírez H, Cruz-Hernndez C. Synchronization of chaotic systems: a generalized Hamiltonian systems approach[J]. Int J Bifurcat Chaos, 2001, 11(5): 1381-1395.

[9] Mu X W, Pei L J. Synchronization of the near-identical chaotic systems with the unknown parameters[J]. Applied Mathematical Modeling, 2010, 34(7): 1788-1797.