M变换中的n阶循环群判定

2012-05-22甘欣荣钟寿国

郑州大学学报（理学版） 2012年3期

甘欣荣，钟寿国

(1.武汉科技大学理学院湖北武汉 430065；2.武汉大学数学与统计学院湖北武汉 430072 )

0 引言

定义1映射G(x):D→D. 归纳地定义迭代映射:G1(x)=G(x),Gk(x)=Gk-1(G(x)),k=2,3,…,若G(x)=x(恒等映射),则G(x)为一阶循环群; 若G(x)≠x,G2(x)≠x,…,Gn-1(x)≠x,而Gn(x)=x,则I,G1,G2,…,Gn-1为n阶循环群,称G(x)为n阶循环映射,记为G∈(Cy)n，n≥1.

Möbius变换(M变换)M(z)=(az+b)/(cz+d),其中，a,b,c,d∈C,z∈C∞,ad-bc≠0,全体形成一个M变换群[1-4].M变换的n次迭代在一定条件下形成n阶循环群,对一般的n，其判定条件与结论未见文献报导[3-9],找出这种条件是有理论和实际意义的.

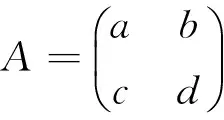
1 An的计算公式

任何方阵的任意次幂(除特殊情形)一般无递归公式.为得到二阶方阵的这个公式，引入2个常数Δ=a+d和δ=bc-ad及与Δ,δ相关的数列Δn,δn,将An的4个元素an,bn,cn,dn均用Δn表达.

引理1对任何正整数n，令

则

an+1=aΔn+δn;bn+1=bΔn;cn+1=cΔn;dn+1=dΔn+δn,

(1)

Δn=ΔΔn-1+δn-1;δn=δΔn-1,

(2)

其中,已令Δ1=Δ=a+d,δ1=δ=bc-ad(≠0), 约定Δ0=1,δ0=0.

引理2对任何正整数n，

(3)

引理1用数学归纳法容易得到它的证明,现证明引理2.

证明要证明(3)，即要证

(4)

(5)

将n=1代入(2)，(4)，(5)直接验证.设(4),(5)对任何自然数n成立，由(2)得

这正是(4)右边用(n+1)替换n的结果.于是(4)得证.(5)的证明方法类似.

2 M(z)∈(Cy)n的判定

定理1(i)M∈(Cy)1⟺a=d≠0,b=0,c=0(此条件简称M1).

(ii)M∈(Cy)n+1(n≥1)⟺M1不成立，Δ1=Δ≠0,Δ2≠0,…,Δn-1≠0，而Δn=0(此条件简称Mn+1).

证明(i) 自明. (ii)当n=1，先证必要性.设M∈(Cy)2，由定义1，M≠I,M2=I，当M≠I,由(i)M1不成立.又由引理1,

(6)

因M2=I，M2仍为M映射[1-4]，由(i)对于M2而言满足M1条件，即

0=a2-d2=(a-d)Δ; 0=b2=bΔ; 0=c2=cΔ

(7)

成立.而刚才已证M1不成立，即或者a≠d,或者b≠0,或者c≠0. 若a≠d，由(7)第1式证出Δ=0;若b≠0,由(7)第2式证出Δ=0;若c≠0,由(7)第3式证出Δ=0.因此无论哪种情形都有Δ=0.n=1的必要性得证.

次证n=1的充分性，即已知M1不成立，Δ=0. 由(i)M1不成立，必有M≠I;又由(6)看出当Δ=0时，A2=δI2(δ≠0)从而M2=I，由定义1，M∈(Cy)2.n=1的充分性得证.

设n≤k命题成立，当n=k+1时，即n+1=k+2，先证必要性.因M∈(Cy)k+2,由定义1，M≠I,由(i)M1条件不成立.故此时M2≠I，刚才已证了M1不成立，那么这时必有Δ1=Δ≠0,否则，若Δ=0，由归纳假设M∈(Cy)2，与假设矛盾.当已证了M1不成立，Δ1≠0,Δ2≠0,…，Δk-1≠0，由于Mk+1≠I,必有Δk≠0，否则Δk=0，由归纳假设M∈(Cy)k+1与假设矛盾.由定义1，此时要求Mk+2=I，由(i)对Mk+2满足M1条件，再据引理1有:0=ak+2-dk+2=(a-d)Δk+1, 0=bk+2=bΔk+1, 0=ck+2=cΔk+1.由已知a=d≠0,b=0,c=0至少有一个不成立，无论哪种情形，刚才所述关于Mk+2的M1条件都得到Δk+1=0，可见，已得Mk+2条件，故n=k+1的必要性得证.

再证n=k+1的充分性.由充分性条件Mk+2，M1不成立及Δ1≠0,Δ2≠0,…，Δk≠0和归纳假设，必有Mm≠I(m=1,2,…,k+1)，由引理1知，

因Δk+1=0，Δk≠0,δ≠0,从而Ak+2=δΔkI2，即Mk+2=I2，于是M∈(Cy)k+2,充分性得证.证毕.