超耦合Burgers方程族及其超Hamilton结构

史 会， 陶司兴

(1.商丘师范学院 物理与信息工程系 河南 商丘 476000； 2. 商丘师范学院 数学系 河南 商丘476000)

0 引言

利用李代数寻找新的Lax可积或Liouville可积系统及它们的可积耦合一直是孤立子理论研究中的一个有意义的重要课题[1-6]. 屠规彰提出迹恒等式来建立连续可积系统或离散可积系统的Hamilton结构[1-2]. 接着不少学者陆续提出迹恒等式的推广形式来建立可积系统的Hamilton结构. 文献[3]发展了迹恒等式并称其为屠格式. 通过利用屠格式及其推广形式, 学者们得到了许多具有物理背景的可积系统. 例如，李代数A1有一组基：

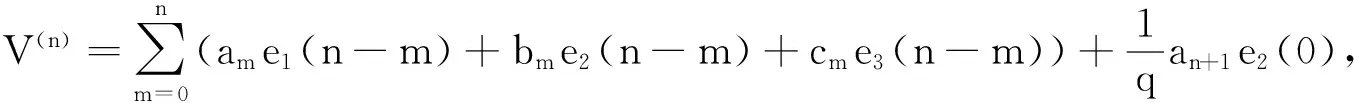
(1)

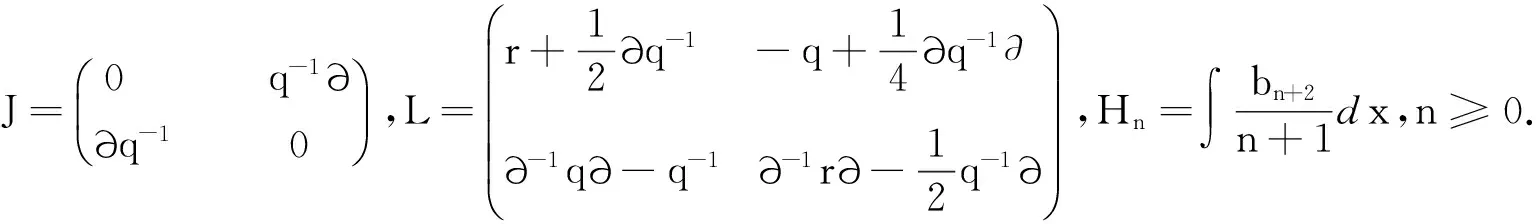
文献[7]首次提出了利用超迹恒等式来建立超可积系统的超Hamilton结构，但是没有给出证明.文献[8]给出了超迹恒等式系统的证明，并且给出了超迹恒等式中常数γ的求解公式， 同时，以超AKNS方程族和超Dirac方程族为例进行了应用.本文将考虑超耦合Burgers方程族及其超Hamilton 结构.

1 超耦合Burgers 程族

考虑李超代数B(0,1)下面的一组基：

[e1,e2]=2e3；[e1,e3]=2e2；[e2,e3]=-2e1；[e1,e4]=[e2,e5]=[e3,e5]=e4；

[e5,e1]=[e4,e3]=[e2,e4]=e5；[e4,e4]+=-(e2+e3)；

[e5,e5]+=e2-e3;[e4,e5]+=[e5,e4]+=e1,

(2)

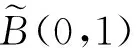
在李超代数B(0,1)的基(2)下, 考虑超等谱问题

φx=Uφ,U=qe1(0)+re2(0)-e2(1)+e3(0)αe4(0)+βe5(0),λt=0.

记

通过求解定态零曲率方程Vx=[U,V],有

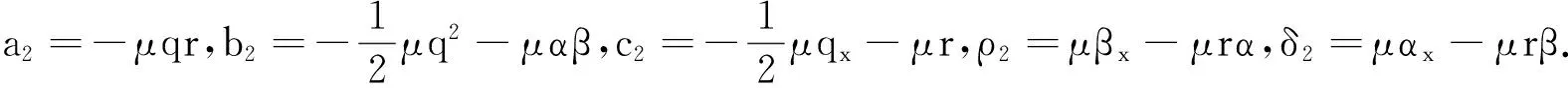
可以得出am+1,bm+1,δm+1和-ρm+1有递推关系:

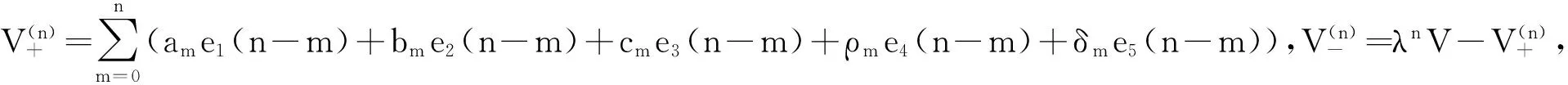
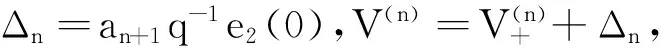
(3)

其中Pn+1满足Pn+1=LPn.如果在方程族(3)中取α=β=0,它可以约化为耦合Burgers方程族(1), 因此称方程族(3)为超耦合Burgers方程族.

2 超耦合Burgers 方程族的超Hamilton结构

假设谱矩阵U定义为

U=U(u,λ)=e0(λ)+u1e1(λ)+…+uqeq(λ),ui∈A，1≤i≤q,

定理1(超迹恒等式)[8]设U=U(u,λ)∈G是齐秩的, 假定定态零曲率方程在相差非零常数倍的意义下有唯一的解V∈G. 那么, 存在一个常数γ使得

(4)

对于任意一个满足定态零曲率方程且具有齐次秩的解，V∈G成立.

定理2[8] 设V是定态零曲率方程的一个解且str(adVadV)≠0, 那么超迹恒等式中的常数可由(5)式给出

(5)

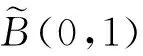
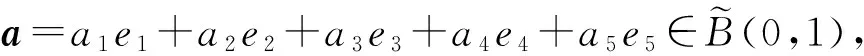
str(P)=P11+P22+P33-P44-P55,

其中,c=(cij)3×3,P=(Pij)5×5,且ab是a和b的矩阵乘积, 则通过计算可得str(adaadb)=3str(ab).

容易计算得:

利用超迹恒等式(4)， 有

比较两边λ-n-1的次数可得

因为str(adVadV)=6u2≠0，利用计算公式(5), 可以得到γ=0.因此，

因此, 超可积耦合Burgers方程族(3)具有超Hamilton结构,

特别的, 超可积耦合Burgers方程族(3)具有超双Hamilton结构,

其中第2个超Hamilton算子M为

参考文献：

[1] Tu Guizhang．The trace identity, a powerful tool for constructing the Hamiltonian structure of integrable systems[J]. Journal of Mathematical Physics, 1989, 30(2):330-338.

[2] Tu Guizhang. A trace identity and its applications to the theory of discrete systems[J]. Journal of Physics A: Mathematical and General, 1990, 23(17):3903-3922.

[3] 马文秀. 一个新的Liouville 可积系的广义Hamiltonian方程族及其约化[J]. 数学年刊:A辑, 1992, 13(1): 115-123.

[4] 斯仁道尔吉. 耦合Burgers族约束系统的动力R-矩阵[J]. 内蒙古师范大学学报:自然科学汉文版， 1997, 26(1): 1-5.

[5] 李雪梅, 牛亏环. 广义TD 族及一些非线性演化方程的显式解例[J].郑州大学学报: 理学版, 2007, 39( 3) : 1-6.

[6] 穆扬眉, 王寒梅. 一类孤子方程的Hamilton结构及其Liouville可积性[J]. 郑州大学学报: 理学版, 2009, 41(1):10-14.

[7] Hu Xingbiao. An approach to generate superextensions of integrable systems[J]. Journal of Physics A: Mathematical and General, 1997, 30(2): 619-633.

[8] Ma Wenxiu, He Jingsong,Qin Zhenyun. A supertrace identity and its applications to superintegrable systems[J]. Journal of Mathematical Physics, 2008, 49(3): 033511.

[9] 孙洪洲, 韩其智. 李代数李超代数及在物理中的应用[M]. 北京：北京大学出版社，1999：157-199.