大旋转角三维直角坐标转换的一种线性模型

王传江 王解先 顾建祥

(1.上海市测绘院，上海 200063; 2.同济大学，上海 200092)

三维直角坐标转换中，采用7参数(3个平移参数、3个旋转参数、1个尺度参数)的Bursa-Wolf模型只适用于小角度下的坐标转换，当在两坐标系统下有3个或3个以上公共点，就可解算出7个转换参数。空间大地测量、三维激光扫描、近景摄影测量的交会摄影、测量机器人自由设站以及GIS中，都遇到大量的大旋转角三维直角坐标的转换问题。

在3个或3个以上公共点不共线的情况下对大角度的空间直角坐标转换，一种方法是对非线性模型线性化，陈义等提出了以方向余弦为参数适用于任意旋转角的空间转换方法[3]，姚吉利等提出了罗德里格矩阵代替方向余弦矩阵的方法[4]。另一种通过引入反对称矩阵等方式，形成线性方程解算，姚吉利提出了3维坐标转换7参数直接计算的模型[5]，潘国荣等提出一种基于空间向量旋动理论的三维基准转换模型[6]，秦世伟等提出了以转换矩阵9元素为参数的坐标转换的简便模型，但其在3个公共点时，可能导致矩阵病态[7]。

在3个或3个以上公共点时，提出了通过构建辅助公共点，以平移量及旋转矩阵元素为参数组成线性方程，按最小二乘法完成参数计算及坐标转换，适用于任意旋转角的空间直角坐标转换。

1 数学模型

1.1 辅助公共点的计算：

设3个不共线公共点A1、A2、A3在A坐标系中坐标分别为A1(x1，y1，z1)、A2(x2，y2，z2)、A3(x3，y3，z3)，有A1、A2、A3可形成一个空间平面，其法向量按公式(1)计算

(1)

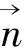
(2)

给定一个合适的距离D，在该直线上距A1点距离为D的空间辅助点FDA1坐标按公式(3)计算

(3)

公共点A1在B坐标系中可按上述方法计算相对应的辅助点坐标，这里距离须考虑比例系数，则D′=(1+m)D；同样，在公共点A2处，按上述思路计算另一辅助公共点FDA2在两个坐标系中的坐标。

由坐标计算距离，通过相应距离的比较得出尺度参数，在文献[4] 、[6]中均有详细论述，设dij、Dij为Ai、Aj两点在坐标系A和坐标系B中的距离，对n个公共点，可计算n(n-1)/2条边比例系数，尺度参数的最佳估计值为n(n-1)/2个尺度参数的平均值，尺度参数可按公式(4)计算

(4)

1.2 空间转换的数学模型

设有两个空间直角坐标系分别为O-XYZ和O′-X′Y′Z′(如图1所示)，两空间直角坐标系间有七个转换参数(3个平移参数、3个旋转参数和1个尺度参数)。

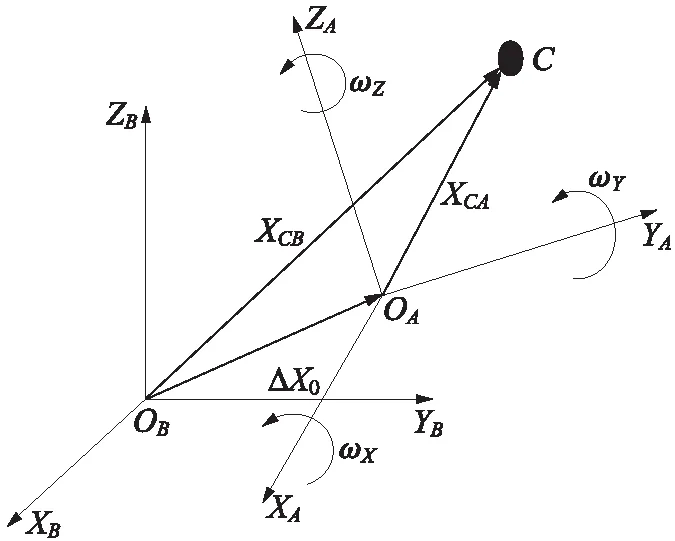
图1 空间转换

由空间直角坐标系A到空间直角坐标系B的转换关系为

(5)

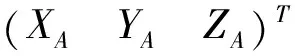
R(ωX).R(ωY).R(ωZ)为旋转矩阵，记为R=R(ωX).R(ωY).R(ωZ)。

(6)

以R中9个元素为参数，将1+m乘入矩阵中各元素中，令

(7)

将(7)式代入公式(5)中，以平移3参数及旋转矩阵9参数共12个元素为未知参数，则公式(1)可写成如下形式

(8)

式中：X1×12=[a11a12a13a21a22a23a31a32a33ΔX0ΔY0ΔZ0]T

当有不共线3个公共点时，按公式(3)计算出2个辅助公共点，则由这5个公共点根据公式(8)可组成15个方程，按最小二乘法计算出X1×12；同上，当有n个公共点，可组成3(n+2)个方程，完成参数计算及坐标转换，计算出旋转矩阵后，由公式(6)可计算3个旋转角。

2 数据验证

为验证坐标转换模型的正确性和可靠性，采用文献[3]中的数据，节点的设计坐标和实测坐标见表1，文献[3]算法与本文算法分别计算的转换坐标及较差数据见表2。

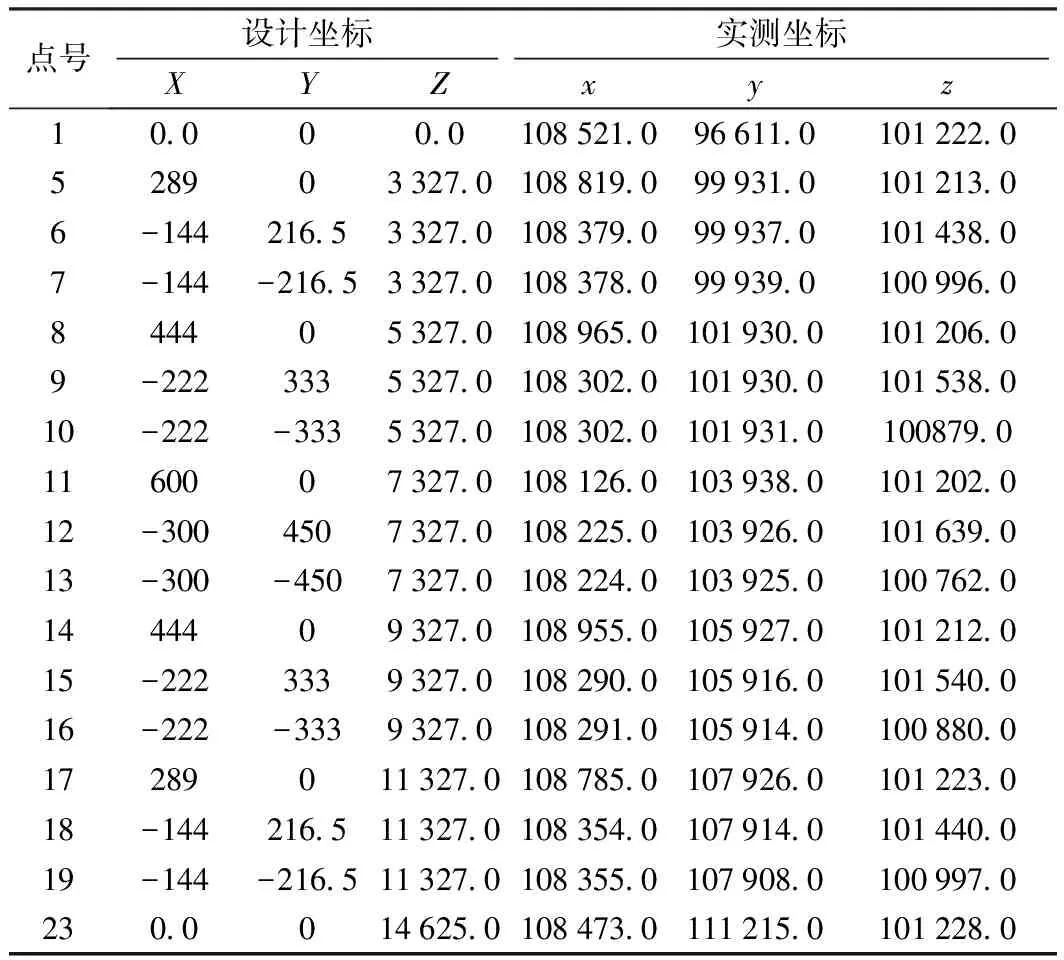
表1 节点的设计坐标和实测坐标 mm

由表1数据按上述坐标转换公式求得的转换参数为

(1+m)=1.001 442 289 3

旋转矩阵

R=

根据计算结果，本文算法可实现三维直角坐标的数据转换，表2数据表明，二者的转换精度基本一致。

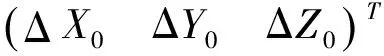
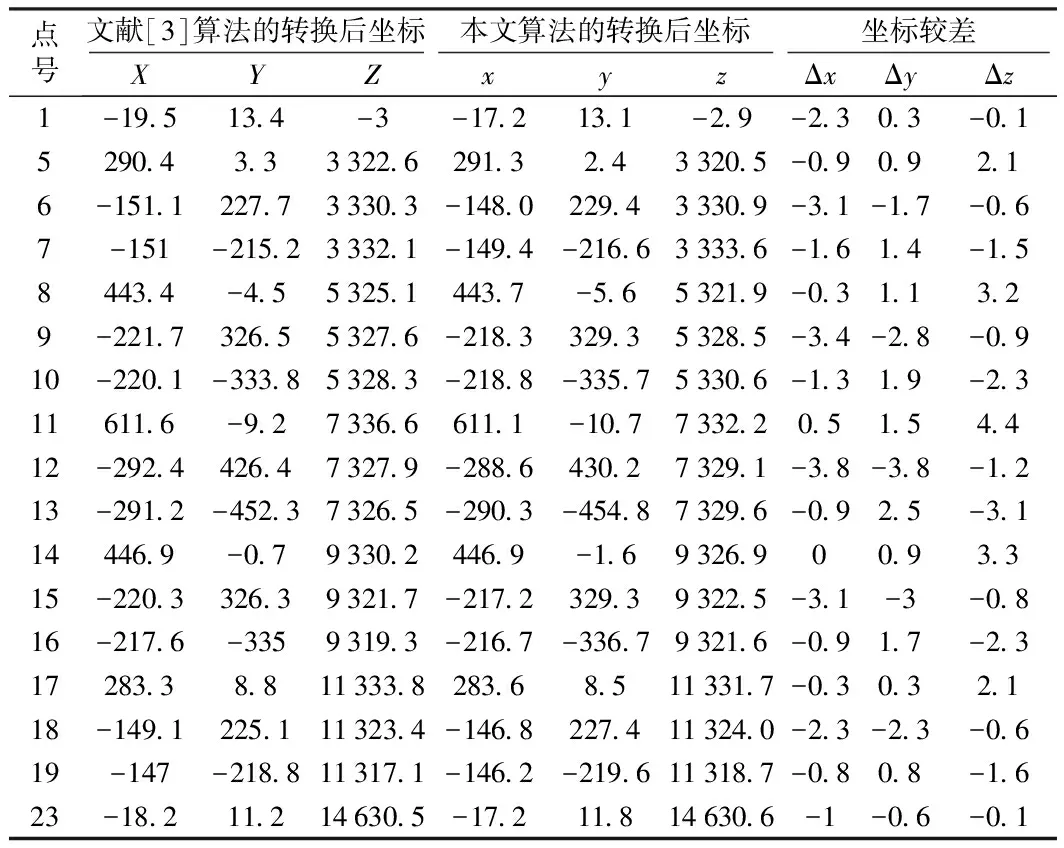
表2 转换后的节点坐标和坐标较差 mm

3 结论

将空间直角坐标转换问题从非线性的的形式转化为线性的、参数相关的形式，使解算公式简单明了，避免了采用非线性方程线性化迭代求解的模型对参数初值、迭代收敛等问题的考虑，经实测数据及模拟数据检验，算法解算精度较好，可靠性高。在3个或3个以上公共点的情况下，模型可完成任意角度情况下的三维直角坐标的转换，对工程应用有参考意义。

参考文献

[1] 李征航，黄劲松.GPS测量与数据处理[M].武汉：武汉大学出版社，2005

[2] 朱华统，杨元喜，吕志平.GPS坐标系统的变换[M].北京：测绘出版社，1994

[3] 陈义，沈云中，刘大杰.适用于大旋转角的三维基准转换的一种简便模型[J].武汉大学学报：信息科学版，2004，29(12)：1101-1104

[4] 姚吉利，韩保民，杨元喜.罗德里格矩阵在三维坐标转换严密解算中的应用[J].武汉大学学报：信息科学版，2006，31(12)：1094-1096

[5] 姚吉利.3维坐标转换参数直接计算的严密公式[J].测绘通报，2006(5)：7-10

[6] 潘国荣，赵鹏飞.基于空间向量的三维基准转换模型[J].大地测量与地球动力学，2009，29(6)：79-82

[7] 秦世伟，谷川，潘国荣.任意旋转角坐标转换的简便模型[J].工程勘察，2009(6)：62-65

[8] 王解先.七参数转换中参数之间的相关性[J].大地测量与地球动力学，2007，27(2)：43-46

[9] 王保丰，徐宁，等.两种空间直角坐标系转换参数初值快速计算的方法[J].宇航计测技术，2007，27(4):20-24

[10] 孔祥元，郭际明，刘宗泉.大地测量学基础[M].武汉：武汉大学出版社，2005