桥补结合电路技术在力传感器中的应用及分析

李育德，米哲敏

（1.太原理工大学 材料科学与工程学院，太原030024；2.同济大学 电子与信息工程学院，上海201804）

在做力及重量测量时，习惯的做法是将受力传感器的输出信号（传感器信号）直接传送给测量系统的前级放大部分，传感器与测量系统之间仅仅保持有简单的信号传递关系，且传感器只有力、电转换作用。尽管当代仪表技术已经进入智能化时代，并且达到尽善尽美的水平，但要实现高精度测量的同时对传感器也提出较为苛刻的要求；而要想使传感器获得设计水平，仪表必须提供出高质量、高稳定的使用参数与条件。之所以互相要求条件之高，其根本原因是由于传感器与仪表二者之间不存在模拟量平衡关系。

1 桥补结合电路及构成

由电阻应变片所组成的直流惠斯顿电桥（以下简称电桥）就是要产生因力作用于受力模型弹性体变形而相应使桥路输出信号，这样就直接把测力的过程简单地转变为测电的过程了。被测对象的转变必然带来测量方法与方式的不同，其误差表达形式及计算过程等诸多因素均会对测得结果产生影响，这是因为直接测量转变成间接测量而造成的。桥路问题是个古老的话题，为完善这一技术手段，多年来推出了非常多的解决问题的方法、思路；得出了相应的应用条件、公式及定理，并获得很好的效果。在当今仪器、仪表高度发达的同时有必要对桥路作更深一步的研究，以便充分地倍加掌握这一经典技术。

图1 桥补结合电路

以四个传感器组成一台测力装置系统为例说明。作桥补结合电路（以下简称桥补电路），如图1所示。图中：R1－1，…；R2－2，…；R3－3，…；R4－4，…代表各传感器同一位置（名）上的应变计，RS为补偿电压的采样电阻、RSδ为补偿电阻。从图中可以看出，桥补电路是由电桥与补偿回路两部分构成，并通过采样电阻RS把这两部分结合在一起的。当力W作用于传感器后引起电桥输出，使得后续测量电路得到一个输入电压信号UAB而引起数字补偿系统工作，补偿电阻RSδ是以数字形式对电桥输出信号进行自动补偿的（该补偿是较为复杂的单元技术，为文字叙述方便，采用电位计的直观图形来代表该单元的转换作用），直至达到电位VB＝VA时补偿自动停止，显示部分同步显示出测量数值。

2 桥补电路性能分析

从图1可以看出，构成桥补电路的前提条件就是将各传感器的四个应变计按“同一位置”的原则串接（或并接）来组成一个桥臂，然后再把组成的四个桥臂搭成一个电桥。这样我们可以得出图1的简化图，如图2所示的桥补电路。在这个桥补电路图中，∑Ri｜i＝1，2，3，4表示同一位置的应变计阻值之和；∑ΔRi｜＝1，2，3，4表示同一位置的应变计阻值变量之和，用ΔRS取代补偿回路RS∥RSδ，∑RL，∑RR分别表示左、右半桥应变计阻值之和；∑ΔRL，∑ΔRR分别表示左、右半桥应变计阻值变量之和。

图2 桥补电路

尽管力学模型元件可以做出许多样式，但目前还是以通过测弯、剪、轴向以及它们的组合为主要的途径来完成弹性元件的设计，并且本着使电桥输出最大为目标来合理粘贴应变计的。讨论电桥输出电压与桥路阻抗内在关系非常有必要，对了解桥补电路的实质内容很有帮助。

2.1 电桥四臂应变相等时的输出

电桥四臂应变相等时，此时电桥习惯地称为等臂全桥，常用的双孔弯曲梁传感器（S型传感器）便是应用的实例。设有一组已按图2所示接好的传感器，同时做出该电路的等效电路，见图3所示。从a，b点看，把该电路可以分成应变电路与补偿电路两部分，当电路工作时，从平衡角度理解可以产生如下等式。

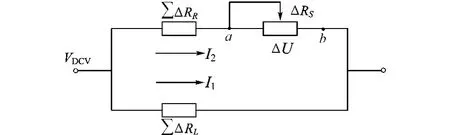
图3 桥补等效电路

应变电压：

只有当ΔUab＝ΔU时可得出平衡方程，应变电压平衡方程：

由于电桥存在着原始不平衡，使得电流表现出如下关系：

又因是等臂全桥，则有下述条件成立：

做一些代换可得以下方程。

应变电阻平衡方程：

在传感器仅重力作用时∑RR，∑RL值是不变的（应变电阻代数和为零），所以可得表达式：

式中：常数因子

通过上述平衡方程式（1），（2）及［结论1］表达式演变可以看出，当有常数因子K存在时所做的测力或称重的测量过程，在桥补电路里可表现为可以用ΔRS电阻的形式来补偿∑ΔR的应变电阻量使得电桥恢复平衡的过程。在这种情况下，就可以把电桥的补偿不再看成是电压补偿而变为电阻补偿，通过电阻补偿使电桥恢复平衡。通俗地讲就是，因电桥阻值发生了∑ΔR量的变化使VA离开原平衡点，通过调节△RS而产生∑ΔRS的效应使VB重新与VA平衡。这样，补偿回路自然便成为电桥的一部分，这就是桥补电路不同于电桥之处，也是桥补结合电路的基本特点。

2.2 左、右半桥应变不相等时电桥的输出

这种情况，常用的柱环式传感器便是例子。这时，下述条件成立：

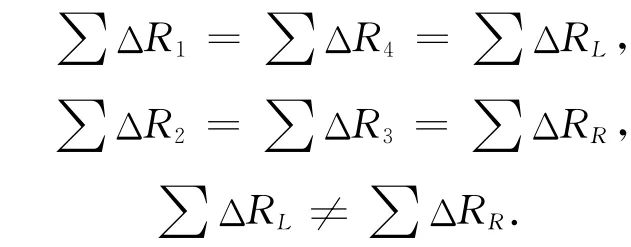
这类电桥称为第一对称全桥［3］。

此类型桥路的应变电阻平衡方程：

因为当有重力存在时∑RR，∑RL值不变，所以有恒等式：

但是，∑ΔRL，∑ΔRR的改变是呈线性状态变化的，因而可以令：

式中：常数因子K＝C＋P.

比较两个结论表达式完全相同。此时同样可得出上述理论结果，它仍然是电阻的平衡过程。

3 同半桥中两臂应变不相等时电桥的输出

圆柱型、圆筒型传感器就是属于此类情况的典型例子。这类传感器的应变计粘贴有竖向及横向之别而组合成非对称电桥。应用材料力学知识可知，在同一力的作用下竖向的应变量值将大于横向值，也就是泊桑效应。对于制做传感器的钢质材料来说其相应的泊桑系数μ＝0.24～0.30范围，在这一前提下，完全可以做到以下条件成立：

第一，桥臂应变值 ∑ΔR1，∑ΔR2，∑ΔR3，∑ΔR4都是线性变化的。

第二，同时保证实现相关关系成立，即

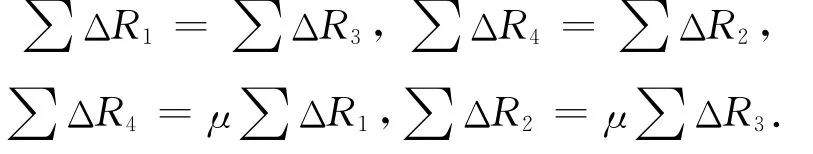
但是，正因为泊桑现象的存在，使得在传感器受力后产生了臂阻抗变化不平衡现象。图4是以D点为参考点比较受力前后A，B两点阻抗变化矢量图，从图中看到，受力前A，B两点同时处于某一定义平衡状态，但在受力后则分别从原来的A，B点移至A′，B′两点，产生了一些不平衡现象：

且存在着∑ΔR4＝μ｜∑ΔR3｜的关系，这样最终导致｜B－B′｜＞｜A－A′｜的结果。

图4 臂阻抗矢量变化

在上述2.1与2.2小节中谈到仅当重力存在时∑RR，∑RL值不变，存在着一个比值常数。但在该例子中∑ΔRL，∑ΔRR值因受到∑ΔR4＝μ∑ΔR1，∑ΔR2＝μ∑ΔR3关系的影响而不在保持恒定，这样是否导致∑RR／∑RL比值也会受到同样的影响而不表现不变性。

设，在传感器受力前比值为：

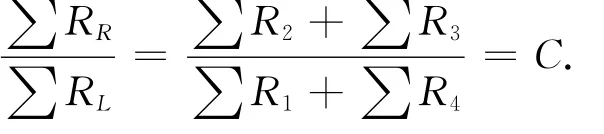
在传感器受力后左、右半桥阻抗为：

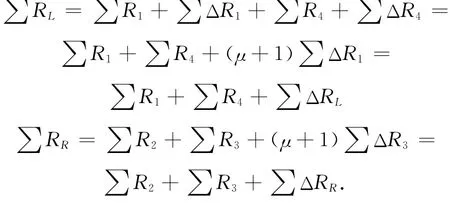
其比值为：

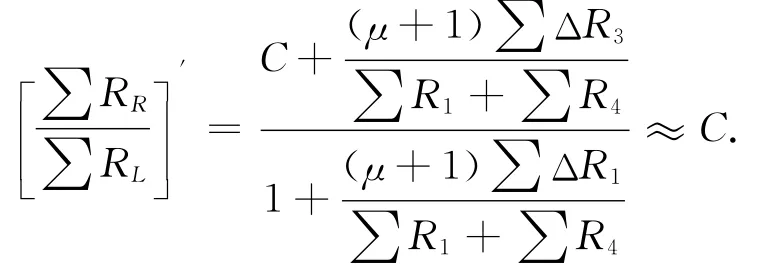
这样可以认为 ∑RR／∑RL比值受重力的影响可忽略不计。

该类型桥路的应变电阻平衡方程：

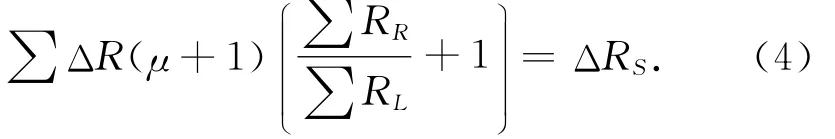
因对某一个传感器来说μ值是恒定的，这样可得表达式：

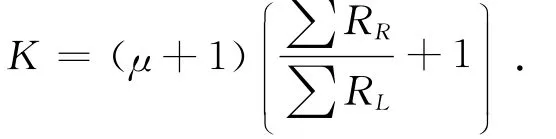
式中：常数因子同样可得出上述的理论结果，称重和测力过程仍然是电阻的线性补偿和桥路电阻的线性平衡过程。

4 结论

电阻应变式测试技术中等臂全桥、对称全桥以及非对称全桥是常用的电桥电路，针对这三种电路使用的广泛性及覆盖性的特点，分别逐一地论证实现桥补结合电路的可能性（上述三个结论的导出充分表明了可能性）。这样就可以实现在电阻应变式测试系统中，仅对电源提出能保证测量的灵敏度就行了的唯一要求。这也是桥补结合电路的特点之一。

桥补结合电路技术的的成功实现后，完全可以克服传统的惠斯顿电桥所表现出难以弥补的一些不足之处，并对测试技术带来了某些改进。

［1］ 秦曾煌.电工学［M］.北京：高等教育出版社，1999.

［2］ 康华光.电子技术基础［M］.北京：人民教育出版社，1982.

［3］ 王化祥，张淑英.传感器原理及应用［M］.天津：天津大学出版社，1990.

［4］ 袁希光.传感器技术手册［M］.北京：国防工业出版社，1986.

［5］ 机械工业部仪器仪表工业局.非电量电测变换技术［M］.北京：机械工业出版社，1988.