近自然护岸措施对提高河岸平衡坡度的作用——以重庆市长寿区桃花溪河岸为例<br/>

近自然护岸措施对提高河岸平衡坡度的作用——以重庆市长寿区桃花溪河岸为例

2012-05-12朱蔚利王云琦雷声坤

中国水土保持科学 2012年3期

朱蔚利，王云琦，雷声坤

(北京林业大学水土保持学院，水土保持与荒漠化防治教育部重点实验室，100083，北京)

河岸带作为滨水区域中适宜植物生长的地区，不仅为动物提供了栖息场所，也是陆生和水生动植物活动迁移的廊道，在生态系统中占据非常重要的地位。护岸类型可分为传统护岸和近自然护岸。李力等［1］、韩素珍等［2］认为，传统护岸只注重行洪、排洪能力，截弯取直、水流速度的加快也会加快水资源的流失，采用混凝土护岸，不利于河道的美化，缺乏亲水性，缺少对环境、生态的考虑，破坏了生物的栖息场所，而近自然护岸对岸坡稳定、景观效果、生物多样性等都有很好的改善作用;因此，基于维持河岸带生态功能的生态护岸显得尤为必要，河道整治中的河道护岸技术正在由原来的纯工程性措施向生态护岸技术发展。尽可能保持河道的原地形地貌及生物多样性已成为国际上治理河道的准则。护岸起着防止水土流失、防洪泄洪的作用，其稳定性直接关系到人民生命财产的安全，因此，结构的稳定与安全是设计中重点考虑的方面。河道岸坡稳定是评价河道岸坡健康的重要指标之一。谢礼明等［3］认为，岸坡稳定因素主要受岸坡土层抗冲刷能力、岸坡坡度等的影响。欧文昌［4］认为，影响梧州市河西防洪堤岸坡的因素有岸坡自然坡度、水流的冲刷、土壤的强度等。谢辉等［5］认为，影响岸坡稳定的因素有水流因素、岸坡坡度、土壤的抗冲刷能力。王玉杰等［6］认为，坡地自身具有维持一定坡度的能力，超过一定坡度后坡地就会失去稳定性，这个坡度在这里称为相对平衡坡度，是判断岸坡稳定性的一个重要指标。河道岸坡护岸不仅要注重其安全稳定性，也不能忽视良好的景观生态功能所带来的附加价值，城市河道岸坡的生态功能越来越被人们所重视;但关于河道岸坡近自然护岸措施下其岸坡稳定性的研究较少，故笔者综合前人对岸坡近自然护岸措施及岸坡稳定性的研究成果，采用针对水力侵蚀的泥沙起动模型和针对重力侵蚀的土壤抗剪强度模型，以重庆市长寿区桃花溪沿岸为研究区，选择自然原型护岸、天然材料织物垫护岸、土工织物扁袋护岸3种近自然护岸措施，对河道岸坡稳定性进行分析，以评价各种护岸措施对增强岸坡稳定性的效果。

1 研究区概况

研究区为长江中上游重庆长寿地区，该地区热量丰富，降水充沛，常年平均气温17.7℃，最高年20.4℃，最低年16.7℃，常年平均降水量1 165.2 mm。长寿境内河流众多，水资源丰富，其中桃花溪多年平均流量5.3 m3/s。

2 研究方法

2.1 护岸措施布设

于2009年3月在重庆市长寿区桃花溪河岸沿水流方向布设了以下3种近自然护岸措施，并以对岸的裸地作为对照。护岸措施布设2年后，对各岸坡的相对平衡坡度进行研究。

1)自然原型护岸措施。采用乔灌草混交模式，种植毛竹(Phyllostachys heterocycla cv.pubescens)、垂柳(Salix babylonica)、毛叶丁香球(Ligustrum quihoui)、黄花槐(Cassia pumila)、鸢尾(Iris japonica)、黑麦草(Lolium perenne)、锯锯藤(Galium aparine var.tenerum)等植物。

2)天然材料织物垫护岸措施。平整岸坡的小沟壑，沿水平线由坡底到坡顶平铺麻袋布，用木芙蓉(Hibiscus mutabilis)、黄花槐等枝条扦插固定，最后播撒黑麦草草种。

3)土工织物扁袋护岸措施。把可降解的麻袋布包裹在坡面展平后填土，然后把土工织物向坡内反卷，包裹填土，在呈阶梯状排列的织物扁袋之间扦插木芙蓉、红叶李(Prunus ceraifera cv.pissardii)、黄花槐、秋花柳(Salix variegata Franch)等枝条，并播撒黑麦草草种。

2.2 土壤采集与分析

1)土壤物理性质。在每块样地沿水流方向从坡顶至坡腰随机采集浅层(0～15 cm)15个土壤样品，用筛分法测定土壤团聚体组成，用环刀法测定土壤质量密度。

2)土壤抗剪强度试验。用TSZ30-2.0型台式三轴仪采用固结不排水法在0.08 mm/min剪切速率条件下进行土壤抗剪强度试验，围压控制为50、100、150、200 kPa。试样破坏强度取峰值强度或应力应变曲线上15%应变所对应的强度。

3)土壤抗冲试验。用泥沙起动模型分析岸坡稳定忽略了各护岸措施下植物根系对土壤的固持作用，也忽略了植物枯枝落叶等能防治水土流失的功能，为此，进行原状土抗冲试验，以弥补泥沙起动模型对地表草垫植被固土效应的忽略。由于水流对岸坡的冲刷破坏包括壤中流对土壤的冲刷破坏和地表径流对岸坡的冲刷破坏，针对这2种冲刷形式，抗冲试验分2部分，一部分用来测浅层土(0～15 cm)的抗冲性(针对壤中流冲刷)，一部分用来测地表草垫(植物茎、叶、根等在地表形成的一层织物状结构，即发生坡面流时水流与岸坡的接触面)的抗冲性(针对地表径流冲刷)。天然材料织物垫护岸、土工织物扁袋护岸施工前期，虽然对地表进行了扰动，但施工结束后会在地表铺设一层麻袋布，故进行麻袋布包裹重塑土的抗冲性试验，以模拟麻袋布在施工前期的护岸作用。

取土柱:以实测的自然原型护岸、天然材料织物垫护岸、土工织物扁袋护岸、对照的浅层土壤硬度平均值(14.7、13.3、16.0、15.2 kg/cm2)为依据，在各样地取原状土柱时，先用硬度计测硬度，在能代表各样地硬度平均值点处，用直径7.6 cm的可取下原状土的改进型环刀取15 cm高原状土柱做抗冲试验，每个样地取8个土样做重复。将取得的土柱装入对应直径和高度的劈成1/2的已称量的PVC管内，并用塑料绳把劈开的PVC管系好，一端用纱布包裹，竖直放置于13 cm水深的水盆中，浸泡24 h，再空出多余的重力水，用电子秤称量。

浅层土抗冲方法:把土柱横放在15 cm宽的水槽末端，去掉纱布和上侧的1/2PVC管，使水流最大限度地冲刷土柱的上侧面。水槽坡度与样地坡度保持一致，约为26°，用稳流装置保持水流流量恒定为12 L/min，冲刷时间为3 min，3 min内冲完的以具体冲完时间计算。冲刷结束后再用电子秤称量含饱和水的土柱质量，然后再把土柱分成上(0～5 cm)、中(5～10 cm)、下(10～15 cm)3段，分别称3段含饱和水的质量。在此，认为冲前上、中、下3段土柱的质量相等，从而可进一步算出总土柱抗冲系数及上、中、下层各自的抗冲系数，即每冲掉1 g含饱和水的土质量所需要的水量，用C(L/g)表示。

地表草垫抗冲方法:把土柱的上表面(有草垫的那面)正放在5 cm宽的水槽末端，去掉上侧的1/2PVC管，接下来的操作同浅层土抗冲方法，只是不需要再把土柱分上、中、下3层分别称量。

2.3 模型构建及参数确定

2.3.1 泥沙起动模型构建以王玉杰等［6］在长江中上游花岗岩山地坡面相对平衡坡度研究中所用模型式(1)为基础，对其中的参数进行校正和确定，建立适用于本研究区的泥沙起动模型。

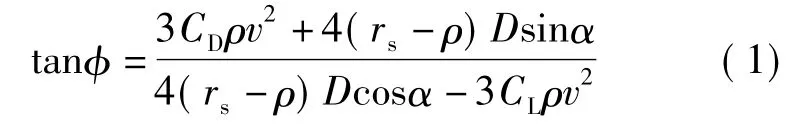
式中:φ为泥沙在水下的休止角，(°);CD为绕流阻力系数;ρ为水的质量密度，g/cm3;v为直接作用在泥沙颗粒上的流速，m/s;rs为泥沙颗粒质量密度，g/cm3;D为泥沙颗粒粒径，mm;α为岸坡的相对平衡坡度，(°);CL为上举力系数。

式(1)中 v、CD、CL、φ 参数值的确定方法视不同情况略有差异，这些参数的确定方法如下:

1)参数v的确定。国内外学者针对坡面流流速开展了大量的研究工作，得到各自的坡面流流速公式，但没有统一的坡面流流速公式，式(1)中所用的v为

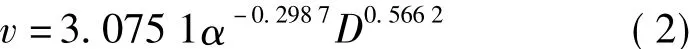
由于研究区域坡面的粗糙系数与该模拟水槽试验不同，且研究区有乔、灌、草，不易进行水槽模拟，所以，采用由Manning公式［7］推导的公式求参数v。

式中:I为单宽降雨强度，m/s;i为单宽入渗率，m/s;H为岸坡坡高，m，根据当地地形条件，为了更好地对比，3种措施及对照的岸坡坡高统一假设为30 m;θ为岸坡坡度，(°);n为坡面糙率，n与坡面状况有关，坡面有矮草，n=0.030，矮丛林稀疏多杂草，n=0.035，有稀疏小树，n=0.050，开挖坡面清洁，经过风雨侵蚀，n=0.018［8］。

2)参数CD与CL的确定。明渠雷诺数表达式为

其中，明渠断面的特征长度为

将式(5)代入式(4)，整理得

式中:R为明渠断面的特征长度，即水力半径，m，坡面流可取径流水深;γ为运动粘滞系数，m2/s，此处取γ=1×10-6m2/s(坡面径流体积与含沙量的比值为 1%，温度为 25 ℃)［8］。

结合当地地形条件，单位宽度(1 m)岸坡汇水面积取1 000 m2，降雨强度取多年测得的最大降雨强度12.5 mm/h，即得单宽降雨强度I为3.472×10-5m/s，于是，Re≈3.47 ×104。

由于坡面上的水流为薄层紊流流态，当沙粒的雷诺数＞103时［6］(Re≈3.47 ×104＞103)，CD=0.43，CL=0.068。

3)参数φ的确定。粒径为0.20～4.27 mm的泥沙，水下休止角［9］为

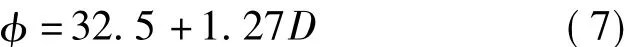
将式(3)、(7)代入式(1)，整理得

各参数取值见表1。

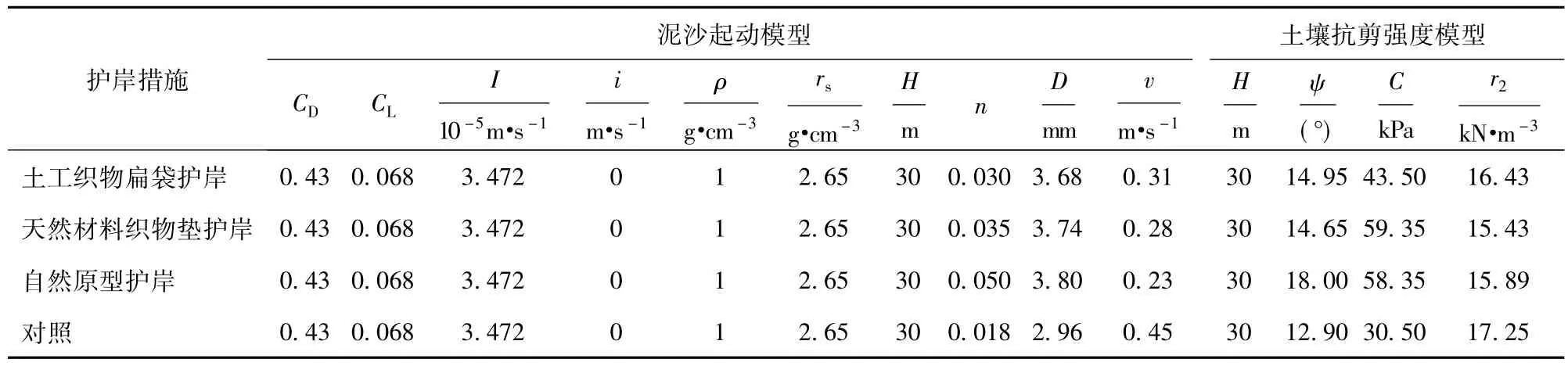
表1 2种模型参数值Tab.1 Parameters of two models

2.3.2 土壤抗剪强度模型构建通过土壤抗剪强度模型推算岸坡稳定有多种模型，每个模型都有不同的适用条件。王玉杰等［6］在研究长江中上游花岗岩山地坡面相对平衡坡度时，采用的模型具有简单易用的特点，模型如下:

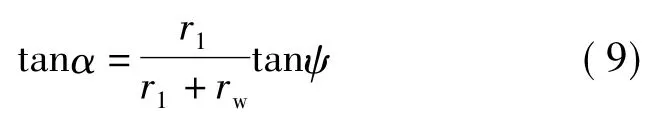
式中:r1为坡面土壤质量密度，g/cm3;rw为水的质量密度g/cm3;ψ为土壤的内摩擦角，(°)。但该模型没考虑黏聚力、岸坡高度对岸坡稳定性的影响，所以，笔者采用赵林海［10］推导出的模型进行岸坡相对平衡坡度分析。

式中:C为土壤的黏聚力，kPa;r2为岸坡土壤的质量密度，kN/m3。

各参数取值如表1。

3 结果与分析

3.1 基于泥沙起动模型岸坡相对平衡坡度分析

采用已建立的模型(8)和模型参数(表1)，计算各护岸措施下的岸坡相对平衡坡度，结果见表2。可以看出，3种近自然护岸措施都能明显地提高岸坡相对平衡坡度。土工织物扁袋护岸措施、天然材料织物垫护岸措施、自然原型护岸措施分别提高岸坡相对平衡坡度 6.8°、7.8°、9.4°。

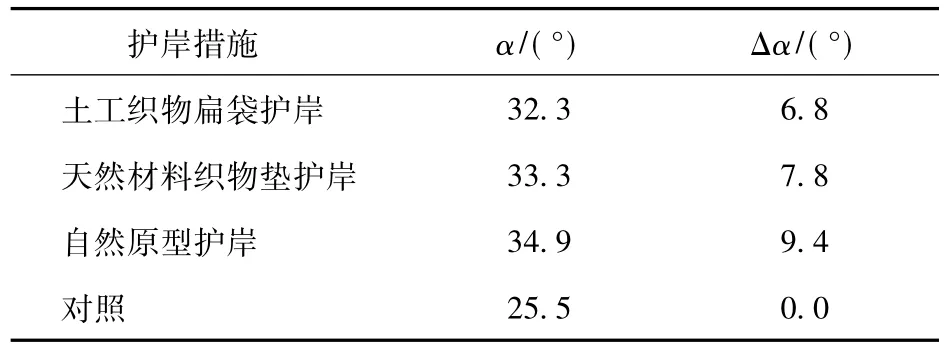
表2 泥沙起动模型得出各措施提高岸坡相对平衡坡度值Tab.2 Increased slope degree of relative balance by three measures using the sediment moving equation

为了找出提高岸坡相对平衡坡度的最主要参数，对部分参数值进行了替换。以土工织物扁袋护岸措施为例，因为土工织物扁袋护岸措施能提高岸坡相对平衡坡度是因为该措施改变了该样地的n和D值，所以，先令土工织物扁袋护岸措施下的 D(3.68)等于对照的D(2.96)，其他参数值不变，计算得出土工织物扁袋措施下岸坡相对平衡坡度为26.7°，对照岸坡相对平衡坡度为25.5°;同样令土工织物扁袋护岸措施下的n(0.030)等于对照的n(0.018)，其他参数值不变，则土工织物扁袋护岸措施下的岸坡相对平衡坡度为31.1°，对照岸坡相对平衡坡度为25.5°。于是，在土工织物扁袋护岸措施下，D、n提高岸坡相对平衡坡度的重要程度Dx、nx分别为:

据此方法得表3。可以看出，在3种护岸措施下，土粒粒径在提高岸坡相对平衡坡度中，重要程度均不到20%;地表糙率在提高岸坡相对平衡坡度中，重要程度超过了80%。

近自然护岸措施能通过改良土壤，提高土壤团聚体含量，增加大颗粒泥沙含量。由式(7)可知，水下的休止角与泥沙颗粒粒径成正比，水下休止角实际上反映了泥沙颗粒的水下摩擦因数［11］，水下休止角越大，泥沙越不易被水流携带，所以，泥沙颗粒粒径影响水下休止角是影响岸坡相对平衡坡度的原因之一。除此之外，泥沙粒径大小对起动流速有很大的影响，即大颗粒泥沙具有更强的抵抗水流侵蚀的能力，因为粒径越大，比表面积越小，泥沙颗粒与水流的接触面越小，所以，水流要推动大颗粒泥沙的运动就需要更大的流速。

另外，由表1可以看出，在各护岸措施下，地表水流流速明显小于对照地表水流流速，地表水流流速与地表糙率有明显的一致性，这说明近自然护岸措施通过提高地表糙率，从而降低地表水流流速，减弱水流搬运泥沙的能力，增强岸坡稳定性，提高岸坡相对平衡坡度。

表3 泥沙起动模型参数对提高岸坡相对平衡坡度的重要程度Tab.3 Increased percentage of slope value of relative balance by three measures using the sediment moving equation

3.2 基于土壤抗剪强度模型岸坡相对平衡坡度分析

将表1参数代入式(10)得到表4。可以看出，通过抗剪强度模型得出3种近自然护岸措施都能提高岸坡相对平衡坡度，土工织物扁袋护岸措施、天然材料织物垫护岸措施、自然原型护岸措施下岸坡相对平衡坡度分别提高 10.4°、6.3°、15.1°，与万士启［12］得出根系可明显提高土的抗剪强度的结论一致，说明植物措施能提高岸坡的稳定性。

抗剪强度模型各因子对提高岸坡相对平衡坡度的重要程度见表5。可知，土壤黏聚力C对岸坡相对平衡坡度的影响最大，内摩擦角ψ次之，土壤质量密度r2最小，说明植物通过死根提供有机质、活根提供分泌物作为土粒团聚的胶结剂，配合须根的穿插和缠结，增强土壤黏聚力，对提高岸坡相对平衡坡度有着重要的作用。

表4 土壤抗剪强度模型得出各措施提高岸坡相对平衡坡度值Tab.4 Increased slope degree of relative balance by three measures using the shear-resistance equation (°)

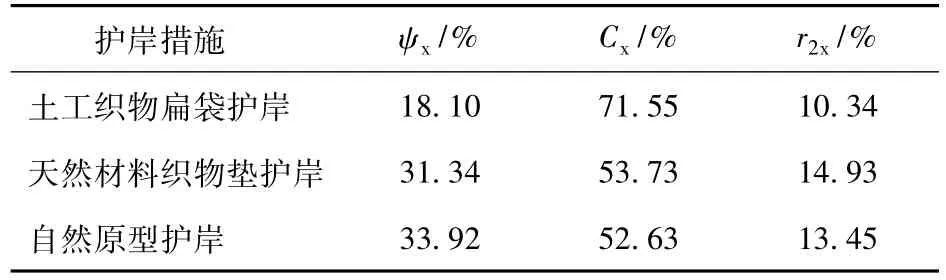
表5 土壤抗剪强度模型参数对提高岸坡相对平衡坡度的重要程度Tab.5 Increased percentage of slope value of relative balance by three measures using the shear-resistance equation

3.3 抗冲性能及其对岸坡稳定性的影响

不同护岸措施土壤的抗冲系数见表6。可知，各近自然护岸措施都能明显提高土壤的抗冲性。浅层土壤抗冲系数表现为自然原型护岸(1 443 L/g)＞天然材料织物垫护岸(1 169 L/g)＞土工织物扁袋护岸护坡(489 L/g)＞麻袋布包裹重塑土(199 L/g)＞对照(12 L/g)，说明有护岸措施的浅层土壤、麻袋布包裹重塑土能抵抗更强的沟蚀及壤中流侵蚀;地表草垫抗冲系数表现为自然原型护岸(4 000 L/g)＞天然材料织物垫护岸(3 200 L/g)＞土工织物扁袋护岸护坡(2 000 L/g)＞麻袋布包裹重塑土(181 L/g)＞对照(12 L/g)。3种护岸措施下土壤的抗冲系数与生物丰富度指数具有一致性。孟凡超等［13］得出这3种护岸措施特征丰富度指数为自然原型护岸(4.09)＞天然材料织物垫护岸(2.05)＞土工织物扁袋护岸(1.79)＞祼地(0.77)。植物根系提高土壤抗侵蚀性能主要是因为根系在土壤中的穿插、缠绕、固结等作用，改变了土壤的理化性质，从而创造了较为稳定的土体结构，特别是根系中D≤1 mm的须根，与土壤的抗侵蚀效能密切相关，被众多的研究者认为是反映土体稳定性的一个重要指标［14］，而样地几种草本植物的根系直径多集中在1 mm以下，尤其0～5 cm土层内集中了90%以上的根系生物量，如表7，解释了0～5 cm土层的抗冲系数大于5～10 cm、10～15 cm土层抗冲系数的现象。

地表草垫、麻袋布包裹重塑土土壤抗冲系数较高，说明其能抵抗更强的溅蚀、面蚀，天然材料织物垫护岸、土工织物扁袋护岸措施布设前期，麻袋布一定程度上能减弱水土流失，植被恢复以后，植被能代替麻袋布的作用，起到减弱水土流失，以达到稳定岸坡的效果。

表6 不同护岸措施土壤的抗冲系数Tab.6 Soil anti-scouribility coefficient under different measures L/g

表7 样地几种植物不同土层根系分布情况Tab.7 Distribution of plants roots in different depths in the sample field

3.4 岸坡稳定性的综合分析

由泥沙起动模型得到3种近自然护岸措施下的岸坡相对平衡坡度为自然原型护岸(34.9°)、天然材料织物垫护岸(33.3°)、土工织物扁袋护岸(32.3°)、对照(25.5°)。由于泥沙起动模型得到岸坡相对平衡坡度是在假设地表为松散颗粒条件下的计算值，而3种近自然护岸措施下的地表及裸地地表均不是松散颗粒结构，由抗冲实验知，良好的地表结构及植被能提高岸坡的抗冲刷能力，故实际值应大于计算值，即岸坡相对平衡坡度的实际值为自然原型护岸＞34.9°、天然材料织物垫护岸＞33.3°、土工织物扁袋护岸＞32.3°、对照＞25.5°。各措施抵抗水力侵蚀和重力侵蚀的岸坡相对平衡坡度见表8。

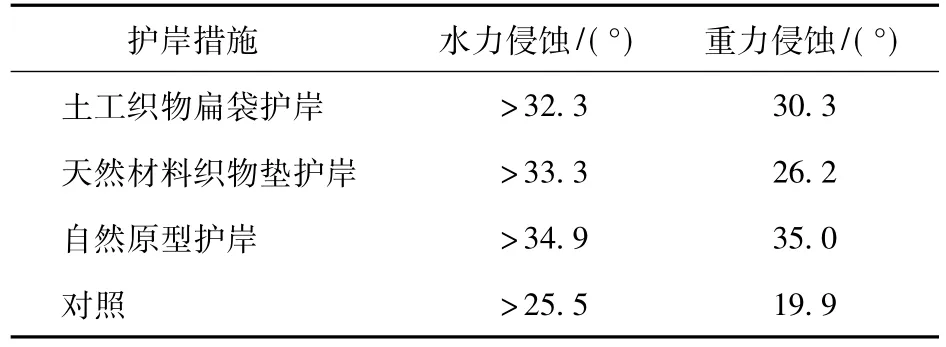
表8 各措施抵抗水力侵蚀和重力侵蚀的岸坡相对平衡坡度Tab.8 Slope degree of relative balance of resisting to water erosion and gravity erosion by different measures

由表8可知，采用泥沙起动模型计算的岸坡相对平衡坡度大于采用土壤抗剪强度模型计算的岸坡相对平衡坡度，由此可初步判定该区岸坡发生重力侵蚀的可能性大于水力侵蚀;所以，以土壤抗剪强度模型得出的结论为依据，土工织物扁袋护岸措施、天然材料织物垫护岸措施、自然原型护岸措施下岸坡相对平衡坡度分别提高了 10.4°、6.3°、15.1°，说明植物通过根系对土壤的加筋、锚固作用，能明显地提高土壤的黏聚力［15］，从而提高土壤的抗剪性能，稳定岸坡。

4 结论

1)泥沙起动模型得出自然原型护岸措施、天然材料织物垫护岸措施、土工织物扁袋护岸措施3种护岸措施作用下的岸坡相对平衡坡度比对照分别提高 9.4°、7.8°、6.8°，与现有研究［16］得出的植被能提高地表糙率，减缓坡面水流流速，减弱水土流失，增强岸坡稳定性的结论一致，且自然原型护岸措施增强岸坡稳定性作用最明显。

2)土壤抗剪强度模型得出自然原型护岸措施、天然材料织物垫护岸措施、土工织物扁袋护岸措施作用下岸坡相对平衡坡度比对照分别提高15.1°、6.3°、10.4°，该模型亦能真实地反映出植被能通过提高土壤黏聚力等作用增强岸坡稳定性。

3)2种模型都能较真实地反映出各岸坡相对平衡坡度，由于泥沙起动模型计算的岸坡相对平衡坡度大于土壤抗剪强度模型计算的岸坡相对平衡坡度，所以，认为该区发生重力侵蚀的可能性更大，故针对重力侵蚀的土壤抗剪强度模型更适合用于该区分析评价岸坡相对平衡坡度。

［1］李力，宁军，张浩.城市生态河道建设方法探究［J］.南阳师范学院学报，2010，9(9):72-74

［2］韩素珍，朱素芬，刘兵.洹河生物护坡河岸景观与生态水利［J］.河南水利与南水北调，2009(12):39-40

［3］谢礼明，李少雄，易发武，等.荆江河段岸坡破坏类型、影响因素及治理措施［J］.人民长江，2009，40(20):4-7

［4］欧文昌.梧州市河西防洪堤岸坡稳定探讨［J］.广西水利水电，1997(3):52-56

［5］谢辉，喻可忠.长江干堤护岸工程施工影响岸坡稳定因素分析［J］.人民长江，2006，37(9):93-101

［6］王玉杰，解明曙，张洪江，等.长江中上游花岗岩山地坡面相对平衡坡度研究［J］.北京林业大学学报，1998，20(6):41-46

［7］李继祥，彭书生，赵三青，等.高速公路路堑边坡的侵蚀临界坡度［J］.辽宁工程技术大学学报:自然科学版，2009，28(1):56-58

［8］吕宏兴，裴国霞，杨玲霞.水力学［M］.北京:中国农业出版社，2002:3-92

［9］中国水利学会泥沙专业委员会.泥沙手册［M］.北京:中国环境科学出版社，1989:30-57

［10］赵林海.土质路基边坡的临界坡度［J］.山西建筑，2004，30(18):66-67