一道天体竞赛题的解法

郑 金

(凌源市职教中心,辽宁 朝阳 122500)

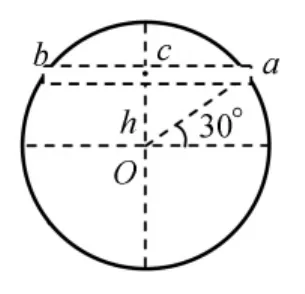
图1

例题.假设地球是一个质量分布均匀的球体,在地球的东半球北纬30°的a处开一条穿过地轴的隧道直通西半球北纬30°的b处,如图1所示.在出口a、b处分别将质量为M和m的两个物体同时由静止释放,已知M＝1.5m,取地球半径R＝6400km,隧道是光滑的,两物体间的碰撞是弹性的,忽略空气阻力和地球转动的影响,问物体m从b处出来后飞离地面的最大高度和射程各为多少？以无穷远处的引力势能为0,距地面高度为H处物体的引力势能为在地球内部距地心为r处的引力势能公式为式中G为万有引力恒量,M0为地球质量,R为地球半径.

解析:首先应用机械能守恒定律和动量守恒定律求m从b处飞出时的速度.物体在地球内部的直线运动过程和在地球外部的曲线运动过程,都遵循机械能守恒定律,但物体在地球内外的引力势能公式不同.设隧道中点c到地心O的距离为h,物体在此点时的速度为u0,则当物体在由洞口a运动到中点c的过程中,由机械能守恒定律有

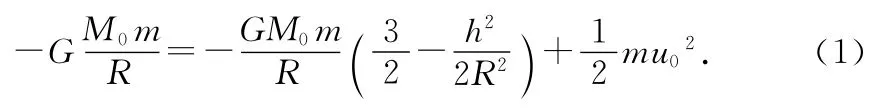
由此得

物体在地面处的重力为

由(2)、(3)式得

由(4)式知,物体到达隧道中点c时的速度与其质量无关.

当两个物体M和m分别在洞口a、b处由静止同时释放时,由于它们的运动情况完全相同,将同时到达隧道中点c处,并发生弹性碰撞.碰撞前,二者的速度都为u0,方向相反,刚碰撞后,两物体M和m的速度分别为v1和v2,取从a→b的方向为正方向,由动量守恒定律有

由机械能守恒定律有

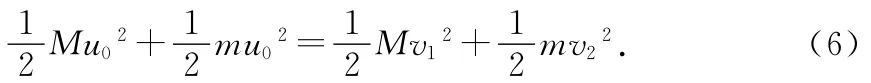
由(5)、(6)式解得

设物体m运动到洞口时的速度大小为v2′,由机械能守恒定律有

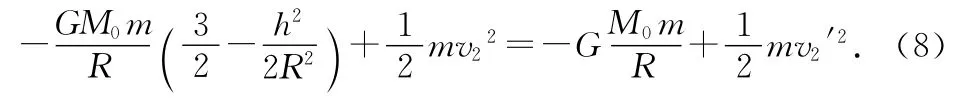
联立(3)、(7)、(8)式解得

而

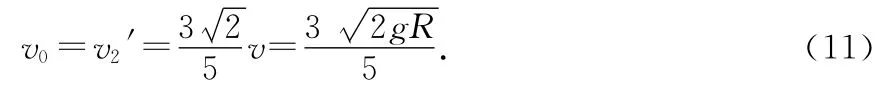
这就是物体从洞口飞出时的初速度.

下面求最大高度.

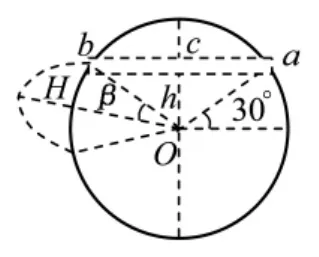
图2

方法1:应用机械能守恒定律和角动量守恒定律.

物体m以v0＝v2′的速度从b处飞出后,在地心引力的作用下沿着椭圆轨道运动,运动轨迹如图2所示.设最高点到地面的垂直距离为H,在最高点即远地点时的速度为v3,由机械能守恒定律有

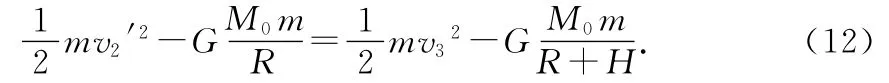
把GM0＝R2g＝Rv2代入得

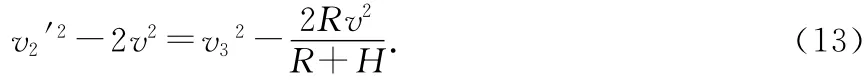
由角动量守恒有

由(13)、(14)式消去v3得

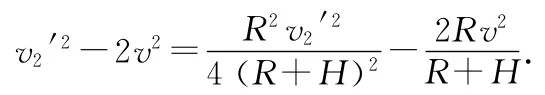
再由(11)式可得

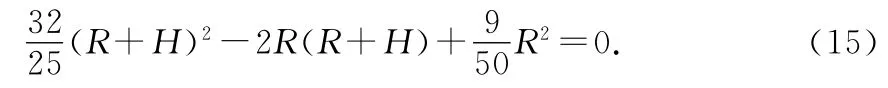
方法2:应用机械能守恒定律、角动量守恒定律和椭圆知识.

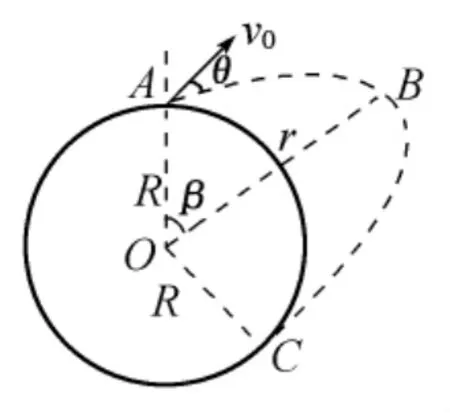
图3

如图3所示,导弹沿着椭圆轨道运动,地心位于椭圆的一个焦点上,在出射点A的速度为v0,利用绕地球做椭圆运动物体的机械能总量公式由机械能守恒定律有.

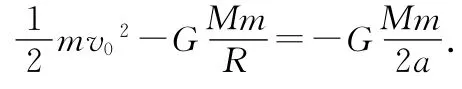
设导弹在最高点B的速度为v3,由万有引力提供向心力得

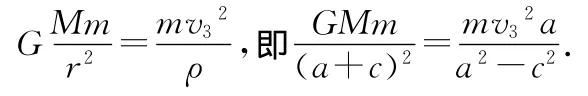
下面求最大射程.

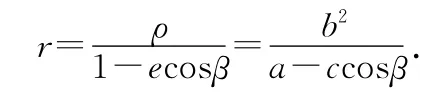
对A点有得则

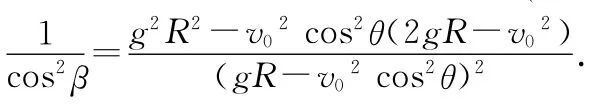
由sm＝R·2β算出最大射程为sm＝4650.24km.若取