一类三阶非线性时标动态方程的振动性*
2012-05-10张少艳王其如
张少艳,王其如
(1.广东金融学院,广东 广州 510520;2.中山大学数学与计算科学学院,广东 广州 510275)
2009年,Hassan在文献[1]中给出了方程
,x(τ(t)))=0
(1)




2010年,Erbe等在文献[2]中也对(1)在(H1)-(H3)成立时进行了研究,给出了异于文献[1]新的振动准则,但文献[2]中同样要求τΔ(t)≥0。其它相关结果,可参见文献[3-10]。

为了书写的方便,我们记x(σ(t))=xσ(t)=xσ。
我们研究的是方程(1)的解的振动性质,所以我们假设上述方程是在无上界的时标上讨论的,即形如[a,∞)的时标。方程(1)的解x(t)称为振动,若x(t)既不是最终正解,也不是最终负解,否则,称x(t)为非振动的。方程(1)称为振动的,如果它的所有解都是振动的。
本文由三部分组成,第一部分为基本引理,第二部分为主要定理,第三部分给出2个应用的例子。
1 基本引理
下面,我们给出第一个引理







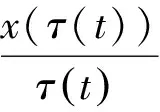

对上式积分可得
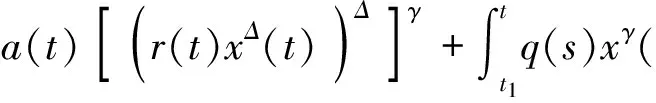





≥
(2)


引理5[3]若x(t)是时标上可导函数,且xΔ(t)≥0,则有下列不等式成立:
(i)若γ≥1,则((x(t))γ)Δ≥γ(x(t))γ-1xΔ(t);
(ii)若0<γ<1且x(t)·x(σ(t))>0,则((x(t))γ)Δ≥γ(x(σ(t)))γ-1xΔ(t).
引理6[4]若x,z是时标上的可导函数,则对x≠0,∀t∈T,有

2 主要结果

[z(s)Q(s)-


证明假设方程(1)的解非振动,不失一般性,我们假设∃T∈[t*,∞),x(t)>0(t≥T),则引理1-3成立。
定义Riccati变换
(t≥T)
(3)
对上式求导可得

由(1)及(H3)可得

由(2)式,可得

(i)当γ≥1时,由引理5可得

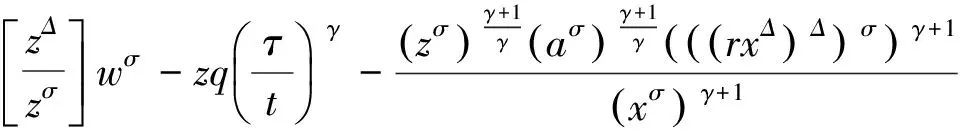


(∵xΔ>0,σ(t)≥t)
(4)


故
≤,xσ≥x
(5)

(6)
(ii)当0<γ<1时,由引理5可得,

由(5)式,xΔ(t)>0及σ(t)≥t可得
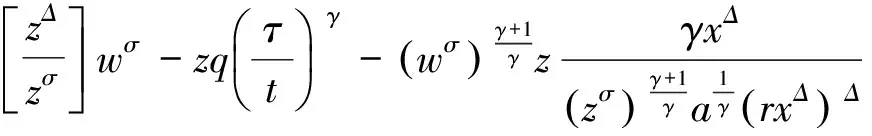
与(6)式相同。由引理2可得
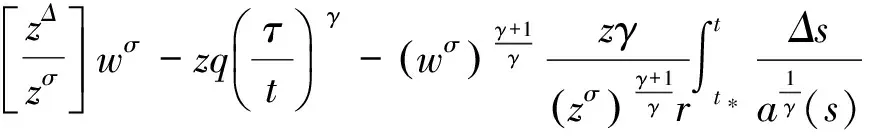
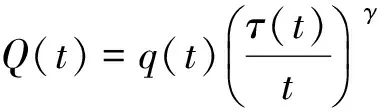



对上式从T到t(≥T)积分,可得


故结论成立。证毕。
下面,我们将给出一个推广的Kamenev型振动准则。
令D0={(t,s):t>s≥t0,t,s∈T},D={(t,s):t≥s≥t0,t,s∈T},H(t,s)∈Crd(D,R),H满足以下条件
(a)H(t,t)=0,(t≥t0);H(t,s)>0,(t,s)∈D;
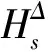

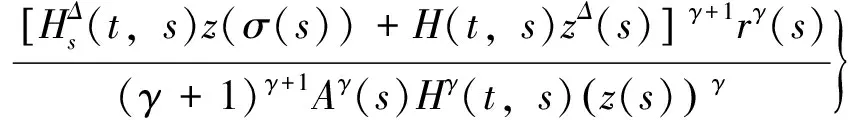

证明由定理1的证明可得



由分部积分公式可得,


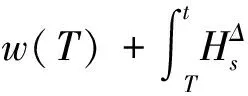
故





故
(t,s)Q(s)z(s)-
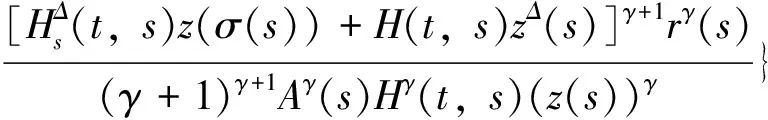
可知与条件矛盾,故方程的解振动.证毕。

成立,若存在一个Δ可导的正函数z,使得
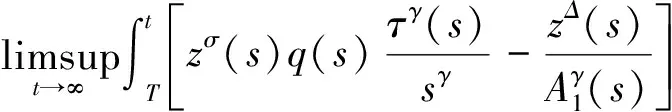

证明假设方程(1)的解非振动,不失一般性,我们假设∃T∈[t*,∞),x(t)>0(t≥T),则引理1-3成立。
定义Riccati变换如(3)式,则可得

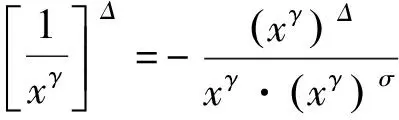
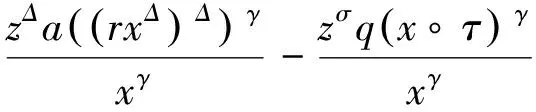


可知与条件矛盾,故结论成立.证毕。
下面将给出γ≥1时的相应结论。

Δs=∞

证明假设方程(1)的解非振动,不失一般性,我们假设∃T∈[t*,∞),x(t)>0(t≥T),则引理1-3成立。
定义Riccati变换如(3)式,由(4)-(6)式可得



由引理2可得

配方得
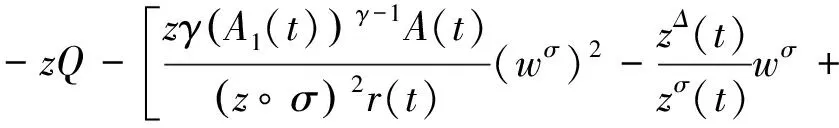

对上式从T到t(≥T)积分,可得

与条件矛盾,结论成立。证毕。
下面我们给出定理4对应的Kamenev型振动准则。

(t,s)Q(s)z(s)-
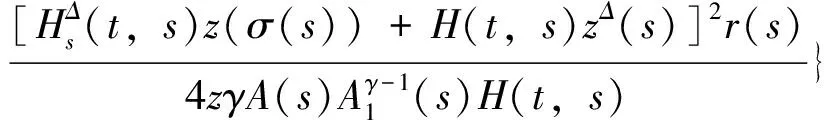
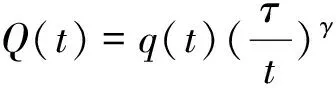
证明假设方程(1)的解非振动,不失一般性,我们假设∃T∈[0,∞),x(t)>0(t≥T),则引理1-3成立。由定理4证明可得



由分部积分公式可得


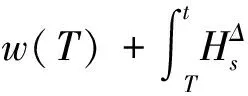
故




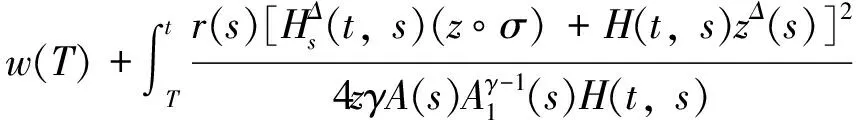
对上式从T到t(≥T)积分,可得
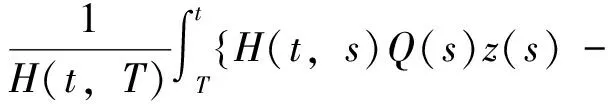
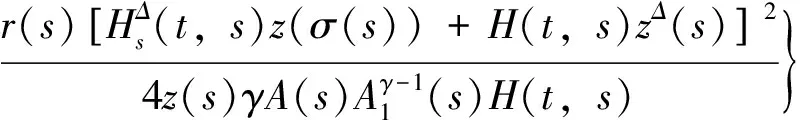
故结论成立。证毕。

Δs=∞
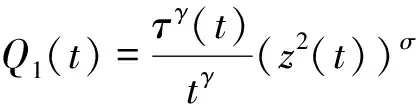
证明假设方程(1)的解非振动,不失一般性,我们假设∃T∈[t*,∞),x(t)>0(t≥T),则引理1-3成立。
定义Riccati变换
对上式求导得


由引理3及引理5-6可得

又由引理2可得

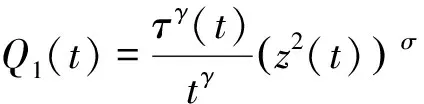

对上式从T到t(≥T)积分,可得

可知与条件矛盾,故结论成立。证毕。
3 例 子
例1 考虑方程
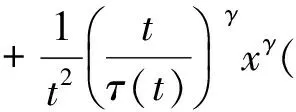
t∈[1,+∞)
(7)

Δs=

故方程(7)的解或振动或趋向于0。
例2 考虑方程

t∈[1,+∞)
(8)

Δs=
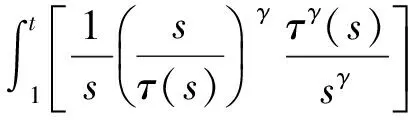
故方程(8) 的解或振动或趋向于0。
参考文献:
[1]HASSAN T S.Oscillation of third order nonlinear delay dynamic equations on time scales [J].Math Comput Model,2009,49:1573-1586.
[2]ERBE L,HASSAN T S,PETERSON A.Oscillation of third order nonlinear functional dynamic equations on time scales [J].Differential Equations Dynamical Systems,2010,18:199-227.
[3]ZHANG S Y,WANG Q R.Oscillation of second-order nonlinear neutral dynamic equations on time scales [J].Appl Math Comput,2010,216: 2837-2848.
[4]AKIN-BOHNER E,BOHNER M,SAKER S H.Oscillation criteria for a certain class of second order Emden-Fowler dynamic equations [J].Electronic Transactions on Numerical Analysis,2010,27: 1-12.
[5]BOHNER M,PETERSON A.Dynamic equations on time scales [M].Birkhäuser,Boston,2001.
[6]SAKER S H,AGARWAL R P,O’REGAN D.Oscillation results for second-order nonlinear neutral delay dynamic equations on time scales[J].Applicable Analysis,2007,86:1-17.
[7]WANG Q R.Oscillation criteria for nonlinear second order damped differential equations [J].Acta Math Hungar,2004,102: 117-139.
[8]WANG Q R.Interval criteria for oscillation of certain second order nonlinear differential equations [J].Dynamics of Continuous,Discrete and Impulsive Systems,Series A: Math Anal,2005,12: 769-781.
[9]WU H W,ZHUANG R K,MATHSEN R M.Oscillation criteria for second-order nonlinear neutral variable delay dynamic equations [J].Appl Math Comput,2006,173: 321-331.
[10]YU Z H,WANG Q R.Asymptotic behavior of solutions of third-order nonlinear dynamic equations on time scales [J].J Comput Appl Math,2009,225 (2): 531-540.
