模糊随机过程函数列均方一致Henstock积分的可积性*
2012-05-10任爱红
任爱红
(宝鸡文理学院数学系,陕西 宝鸡 721013)
Henstock积分又称Kurzwarl积分或广义黎曼积分,Henstock 积分不仅包含牛顿积分、黎曼积分和勒贝格积分,而且不需要测度理论的支持。近年来,许多学者已将其引入到模糊数学领域,并对其理论进行了深入的研究[1-4]。然而与模糊数值函数Henstock积分的研究成果相比,对模糊随机过程均方Henstock积分的研究显得非常欠缺[5-9]。由于收敛定理对积分理论的研究非常重要,因此,研究模糊随机过程均方Henstock积分的收敛定理是非常有意义的。 本文引进了二阶模糊随机过程均方一致Henstock可积的概念,利用均方一致Henstock可积,研究了二阶模糊随机过程均方一致Henstock可积的充分必要条件,得出了模糊随机过程函数列的收敛定理。
1 预备知识
模糊数空间Ed={v:Rd→[0,1]},v满足如下条件:

对于任意的v∈Ed,称[v]α={x∈Rd|v(x)≥α}为v的α水平截集。


设T是一实数集,称X:T→L2为二阶模糊随机过程。若在点t∈T,X关于ρ连续,称X在点t均方连续。若在T上的所有点都均方连续,则称X在T上均方连续(更多结论可参阅文献[5-7])。
本文中,假定对任意的t∈[a,b],H差X(t)ӨX(s)(s 定义1 设δ(x)>0是[a,b]上的一个实值函数,[a,b]的一个划分T={[ti-1,ti];ξi,i=1,2,…,n},如果满足下列条件: (i)a=t0 下面先给出二阶模糊随机过程均方一致Henstock可积的定义。 定义3 设{Xn,n∈N}∈L2是[a,b]上Henstock可积函数列,称{Xn}在[a,b]上均方一致Henstock可积,如果对任给ε>0,存在实值函数δ(t)>0,使得对[a,b]上的任意δ精细划分T={[ti-1,ti];ξi,i=1,2,…,m}及任一n∈N,有 现在我们来证明模糊随机过程函数列均方一致Henstock可积的充分必要条件。 (1) 证明充分性若对任给ε>0,存在实值函数δ(t)>0,对[a,b]上的任意δ精细划分T及T′,上述(1)式成立,则由文献[10]定理3.1.2 可知,每个Xn是[a,b]上均方Henstock可积的。又因δ是共同的,即对任一n∈N成立,所以{Xn}在[a,b]上均方一致Henstock可积。 由三角不等式性,综合以上两式得 因此不等式(1)成立。 下面给出模糊随机过程函数列均方一致Henstock可积的收敛定理。 定理2 设{Xn,n∈N}∈L2是[a,b]上均方Henstock可积函数列,满足 (i)X∈L2,并且Xn(t)以L2收敛到X(t),t∈[a,b],即ρ(Xn,X)→0; (ii){Xn,n∈N}在[a,b]上均方一致Henstock可积。 证明由定理假设条件(ii),函数列{Xn}在[a,b]上均方一致Henstock可积,由定义3可知,对任给ε>0,存在实值函数δ(t)>0,使对区间[a,b]上的任意δ精细划分T={[ti-1,ti];ξi,i=1,2,…,k}及任一n∈N,有 现固定精细划分T={[ti-1,ti];ξi,i=1,2,…,k},由假设(i),Xn(t)以L2收敛到X(t),t∈[a,b],即Xn(t)→X(t)逐点收敛于[a,b],可得 ξi)(ti-ti-1) 对上述极限,取自然数N0,使得对任意n>N0,任给ε>0,有不等式 成立。现在说明Xn(t)在[a,b]上的原函数Gn(a,b)是L2中柯西序列。当n>N0,有 而且,当m,n>N0时,由上述不等式可知 ρ(Gm(b)ӨGm(a),Gn(b)ӨGn(a))≤ 因此{Gn(a,b),n∈N}为L2中柯西序列,于是存在A∈L2,N1≥N0,当n>N1,有ρ(Gn(a,b),A)<ε。 根据以上不等式,有 Gn(b)ӨGn(a))+ρ(Gn(a,b),A)<2ε 定理3 设{Xn,n∈N}∈L2是区间[a,b]上均方一致Henstock可积函数列,若对任给ε>0,存在实值函数δ(t)>0,使得对区间[a,b]上的任意δ精细划分T={[ti-1,ti];ξi,i=1,2,…,m}及任一n∈N,有 ρ[Xn(ξi)(ti-ti-1),Gn(ti)ӨGn(ti-1)]<ε 成立,则对[a,b]上δ精细部分划分T′={[ti-1,ti];ξi,i=1,2,…,s}及任一n∈N,有 (2) 成立,其中l=1,2,…,m。 (3) 由(2)-(3)式得 对任意η>0和所有n∈N都成立,取η=ε,则由上式得 ρξi)(ti-ti-1),Gn(b)ӨGn(a)]<ε 注1 从定理3可知对单个均方Henstock可积函数X,上述定理仍然成立。 文中,通过引入二阶模糊随机过程均方一致Henstock可积的定义,研究了二阶模糊随机过程均方一致Henstock可积的充分必要条件,得出了模糊随机过程函数列的收敛定理。该积分本质上是取值度量空间函数的积分,不需要利用测度理论的支持。根据这种积分的定义和性质,能否给出模糊值过程关于模糊值过程的积分,以及能否定义模糊Brown运动,进而研究模糊值过程关于此模糊Brown运动的积分问题,对于这种有意义的随机风趣的研究,这是我们后续研究工作的重点。 参考文献: [1]GONG Z T.On the problem of characterizing derivatives for the fuzzy-valued functions (II): almost everywhere differentiability and strong Henstock integral [J].Fuzzy Sets and Systems,2004,145: 381-393. [2]GONG Z T,SHAO Y B.The controlled convergence theorem for the strong Henstock integrals of fuzzy-number-valued functions [J].Fuzzy Sets and Systems,2009,160: 1528-1546. [3]FENG Y H.Mean-squares integral and differential of fuzzy stochastic process [J].Fuzzy Sets and Systems,1999,102: 271-280. [4]FENG Y H.Mean-squares Riemann-Stieltjes integrals of fuzzy stochastic process and theirs applications [J].Fuzzy Sets and Systems,2000,110: 27-41. [5]李静,冯玉湖.模糊随机过程的均方Henstock积分[J].东华大学学报,2007,33(5): 590-594. [6]李静.模糊随机过程的均方Henstock积分[D].中国优秀硕士学位论文全文数据库,2007. [7]任爱红.二阶模糊随机过程均方Henstock-Stieltjes积分的收敛定理[J].西南师范大学学报,2011,36(5): 62-66. [8]任爱红.二阶模糊随机过程均方Henstock-Stieltjes积分的相关性质[J].曲阜师范大学学报,2011,37(1): 35-38. [9]任爱红.二阶模糊随机过程均方Henstock-Stieltjes积分[J].甘肃科学学报,2012,24(1): 16-19. [10]吴从炘,马明.模糊分析基础[M].北京:国防工业出版社,1991.
2 主要结果和证明






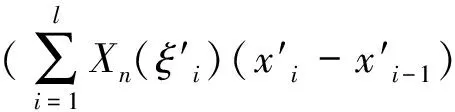


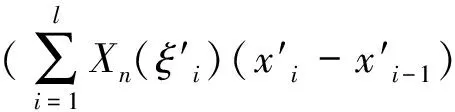

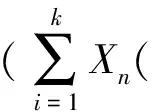
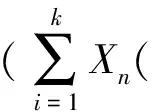

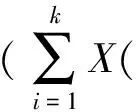

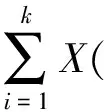
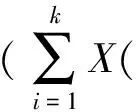



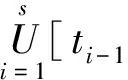

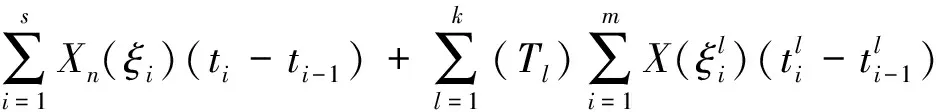

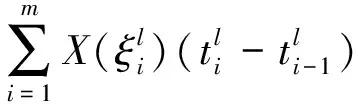

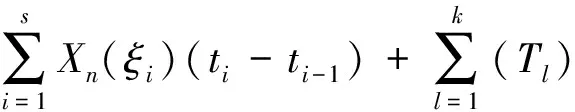
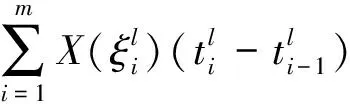
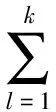
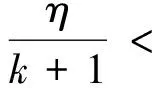
3 结 论
