新疆某砂岩铀矿含矿层孔隙结构的分形特征*

陈 亮, 谭凯旋, 刘 江, 曾 晟

(1. 南华大学 矿业工程博士后流动站，湖南 衡阳 421001;2. 南华大学 核资源与核燃料工程学院，湖南 衡阳 421001)

砂岩的孔隙结构极其复杂。长期以来人们一直采用数理统计方法去描述砂岩的复杂微观孔隙结构，但总不尽人意。分形几何学是20世纪70年代后发展起来的一门新兴学科，是描述复杂的、不规则现象和过程的有力工具。国内外众多学者采用分形理论研究了砂岩的孔隙结构特征，尤其是储层砂岩的孔隙结构特征，取得了较好的研究成果。张婷等[1]利用分形理论研究了储层砂岩的孔隙结构，并通过求取其分维值分析了岩样储集体的物性。李中锋等[2]探讨了砂岩储层孔隙结构的分形特征，研究结果表明其分维值可定量描述孔隙结构的非均质性，分维值越大，砂岩孔隙分布的非均质性越强。张宸恺等[3]应用分形理论研究了鄂尔多斯MHM油田低孔渗砂岩储层的孔隙结构，结果显示两个主要含油气层段的储层孔隙结构存在多重分形特征。文慧俭等[4]的研究也表明同一岩心样品在不同孔径范围具有不同的分形维数。Schlueter等[5]、Radlinski等[6]及Tsakiroglou等[7]也研究了砂岩和储层砂岩孔隙结构的分形特征。

在众多铀矿床类型中，砂岩铀矿床是指工业铀矿化主要产于砂岩中的铀矿床。据新近国际原子能机构网站数据(IAEA-TECDOC-1629报告)，全球1 352个已知铀矿床中，有530个为砂岩铀矿，占全球已探明总储量的27.9%，数量和储量均位居第一。我国近年在北方中新生代沉积盆地发现和探明了6种新的大型、特大型砂岩型铀矿[8]，大大提高了砂岩铀矿在铀资源中的地位，已成为我国4大铀矿主要工业类型之一。目前国内外的砂岩铀矿已广泛采用地浸技术开采[9-10]。含矿层的渗透性是地浸采铀的一个主要影响因素，而其渗透性与孔隙结构特征密切相关。故开展砂岩铀矿含矿层孔隙结构特征的分形研究显得非常必要，而目前国内外在这方面的研究还很少。为此，本文以新疆某砂岩铀矿含矿层为研究对象，利用压汞实验数据，采用分形理论研究含矿层孔隙结构特征，并探讨其与渗透性的关系及成因。

1 材料与方法

新疆某砂岩型铀矿床产于伊犁盆地南缘西部，含矿地层为中下侏罗统水西沟群。中下侏罗统水西沟群为一套陆相含煤碎屑岩建造，由下而上划分为3个岩组(即八道湾组、三工河组、西山窑组)、8个沉积旋回。每个旋回中都发育层间氧化带，铀矿化与氧化带密切相关，所有氧化带都有铀矿化，其中三工河组Ⅴ旋回发育区域性层间氧化带，为主要含矿层。含矿层为中粗粒砂岩，渗透性低，顶、底板为泥岩或泥岩与粉砂岩互层构成。矿体位于氧化带与还原带过渡位置。在矿体及其附近围岩共取6个样品用于含矿层孔隙结构的压汞实验分析。压汞实验使用全自动压汞仪(Autopore IV 9510)，完成于清华大学热能工程实验室。由压汞实验数据计算的含矿层孔隙结构参数见表1。

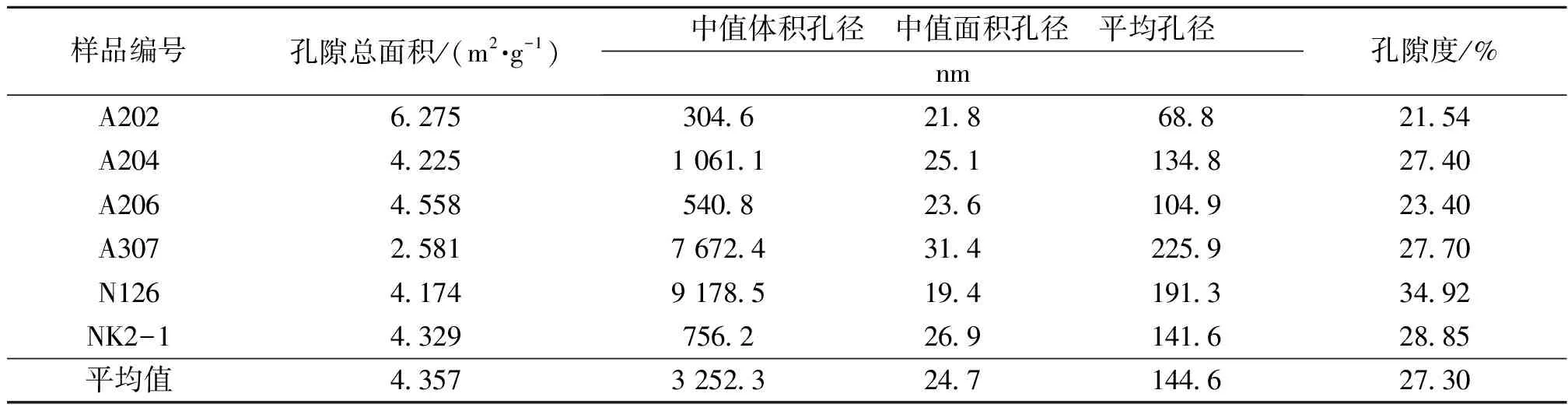
表1 含矿层的孔隙结构参数

2 结果与讨论

2.1 根据汞饱和度与毛细管压力求取分维值

依据分形原理，具有相同尺度物体数量与其测量的线性尺度之间满足幂律关系，即

N(r)∝r-D

(1)

式中：N(r)为分形物体容纳标尺特征体的数目；D为分形物体的分形维数。

根据毛细管模型，有

N(r)=VHg/(πr2l)

(2)

式中：VHg为水银流经半径为r的毛细管所对应的水银累积体积；l为毛细管的长度。

由式(1)和式(2)得

VHg/(πr2l)∝r-D

(3)

VHg∝r2-D

(4)

据Laplace方程可得

Pc=(2σcosθ)/r

(5)

式中，Pc为毛细管压力；σ为界面张力；θ为接触角。

由式(4)和式(5)可得

VHg∝P-(2-D)

(6)

由岩样中水银饱和度的定义有

SHg=VHg/Vp

(7)

式中，SHg为水银饱和度；Vp为样品的孔隙体积。

由式(6)和式(7)可得

表3显示的是特级教师和普通教师心理健康的差异，从健康均分可以看出,特级教师和普通教师心理健康水平有显著差异(P<0.001)。从各因子得分看，除躯体化因子差异不明显外(P>0.05)，其它8个因子都有明显差异。其中，在强迫症状因子上的差异明显(P<0.01)，其余7个因子的差异均是极其显著(P<0.001)，均是普通教师得分明显高于特级教师。

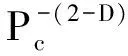
(8)

式中α为常数。

以上分析表明岩样中汞饱和度与毛细管压力之间满足幂律关系，在双对数坐标下二者为一直线，根据直线的斜率可求取岩样的分维值(D=b+2)。样品lgPc-lgSHg关系图见图1。

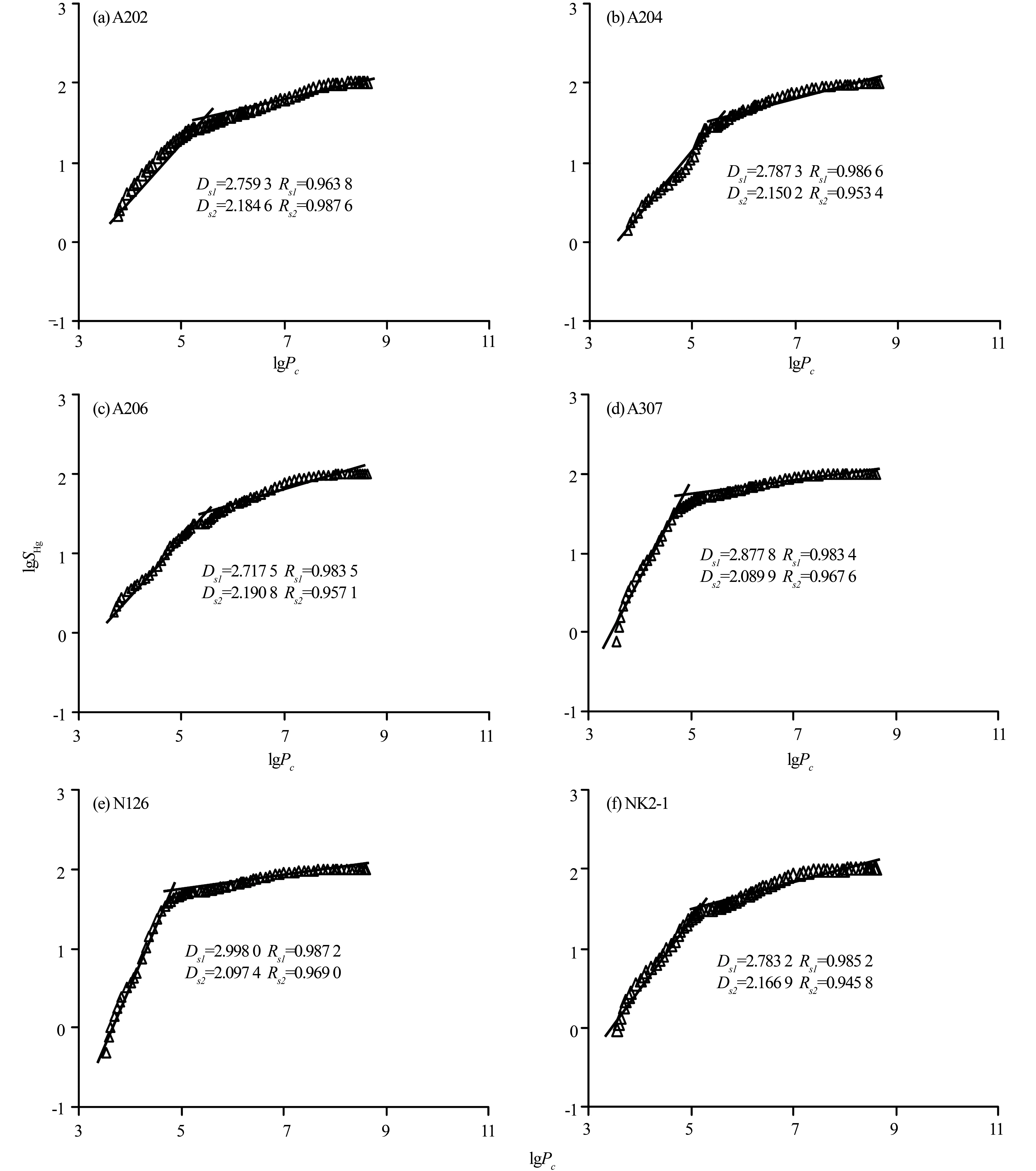
图1 lgPc-lgSHg关系图

2.2 根据孔隙累积体积与孔径求取分维值

设孔隙某一孔径r，半径大于等于r的孔隙数为N(r)，如果岩层孔径分布符合分形结构，则有

∝r-D

(9)

式中，P(r)为孔径分布密度函数；D为分维值。

设V(r)为半径不小于r的孔隙体积，V0为系统孔隙总体积，b为常数，如果

V(≥r)/V0∝rb

(10)

对式(10)两边求导得

dV(≥r)∝rb-1dr

(11)

对式(9)两边求导得

dN(≥r)∝r-D-1dr

(12)

假设岩层孔隙为近似球形，则

dV(≥r)∝r3dN(≥r)

(13)

rb-1dr∝r3r-D-1dr

(14)

由式(13)可得

b=3-D或D=3-b

由式(10)和式(14)可知，测量体积V与半径r存在以下关系

V(≥r)/V0=K1r3-D

(15)

式中K1为常数。对式(15)两边取对数可得

lgV(≥r)=lg(V0K1)+(3-D)lgr

(16)

如果在双对数坐标下V-r存在线性关系，表明岩层孔隙结构具分形特征。样品lgr-lgv关系图见图2。

由上述两种方法求取的样品分维值见表2。

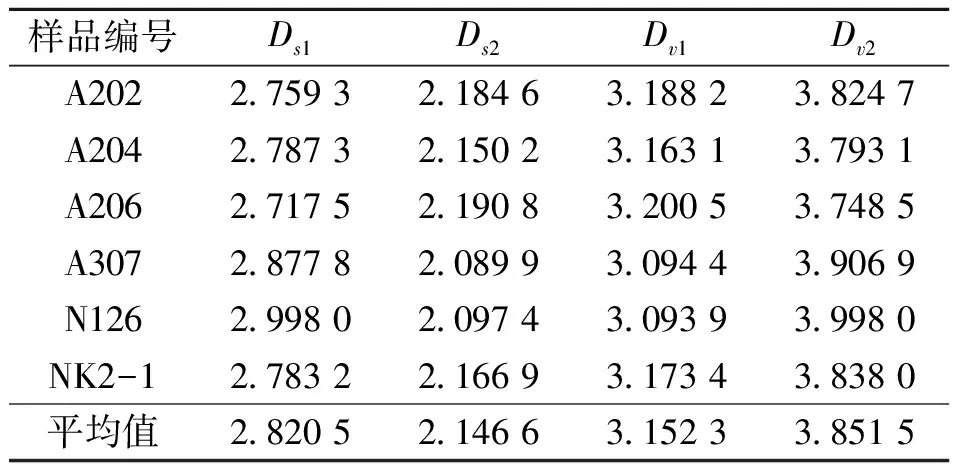
表2 含矿层孔隙结构的分维值

2.3 含矿层孔隙结构的分形特征

含矿层平均孔径在68.8～25.9 nm之间变化，均值为144.6 nm，平均孔径总体较小。孔隙度变化于21.54%～34.92%之间，均值为27.30%。空隙总面积在2.581～6.275 m2/g之间波动，均值为4.357 m2/g。中值体积孔径的变化范围为304.6～9 178.5 nm，均值为3 252.3 nm。中值面积孔径在19.4～31.4 nm之间变化，均值为24.7 nm。

图1和图2的散点均大致分布在二段直线上，即具双分形特征，此时采用分段拟合。其分界点的确定参照申维[11]，并考虑线性拟合程度。Ds1在2.717 5～2.998 0之间变化，均值为2.820 5。Ds2在2.089 9～2.190 8之间波动，均值为2.146 6。Dv1变化于3.093 9～3.200 5之间，均值为3.152 3。Dv2在3.748 5～3.998 0之间变化，均值为3.851 5。Ds1和Ds2的波动范围均不大，表明含矿层孔隙结构总体上具类似的分形特征和形成机理[12]。Ds1明显大于Ds2，说明大孔隙结构的分维值明显大于小孔隙结构的分维值。Dv1和Dv2的变化规律也反映了每个样品总体上的孔隙结构的分形特征差异不大，仅在不同类型孔隙结构之间存在差异，即颗粒间孔隙结构的分维值显著大于颗粒内部孔隙结构的分维值[13]。一般认为颗粒间孔隙要远大于颗粒内部孔隙，因而支持大孔隙结构的分维值大于小孔隙结构分维值的结论。含矿层孔隙度随大孔隙结构分维值的增加而升高，随小孔隙结构分维值的升高而降低(图3)。

2.4 含矿层孔隙结构的分形特征与渗透性的关系

砂岩的渗透性能除与孔隙度相关外，还受孔隙结构复杂程度的影响，包括孔隙表面粗糙程度、分布与形状及连通性等。在三维欧氏空间中砂岩孔隙结构的分维值在2～3之间变化[1]。孔隙结构的分维值可指示其复杂程度，分维值越高，表明孔隙结构越复杂，分维值的低值则说明孔隙结构的复杂程度低[12]。Ds1接近3，表明大孔隙结构的复杂程度高，孔隙表面粗糙程度、分布不均性、形状的不规则程度均高，孔隙连通性差。Ds2接近2，表征小孔隙结构的复杂程度低，明显低于大孔隙结构的复杂程度，孔隙表面粗糙程度、分布不均性、形状的不规则程度均低，孔隙连通性好。Dv1和Dv2的波动规律也表明大孔隙结构的复杂程度明显大于小孔隙结构的复杂程度。Dv1和Dv2在3～4之间变化，而Ds1和Ds2在2～3之间波动，这是由于采用不同的方法求取分维值所致[13]。

在大多情况下，孔隙结构的复杂程度与渗透性呈负相关关系，即孔隙结构越复杂，渗透性越低，孔隙结构复杂程度变低，渗透性变高[12, 14]。如根据小孔隙结构的复杂程度，推测含矿层的渗透性高，而这与实际情况不相符。如依据大孔隙结构的复杂程度，推测含矿层的渗透性低，与实际情况吻合。因此，大孔隙结构的分维值可判定含矿层的渗透性，并且其高值指示渗透性低，而小孔隙结构的分维值不能判定含矿层的渗透性。

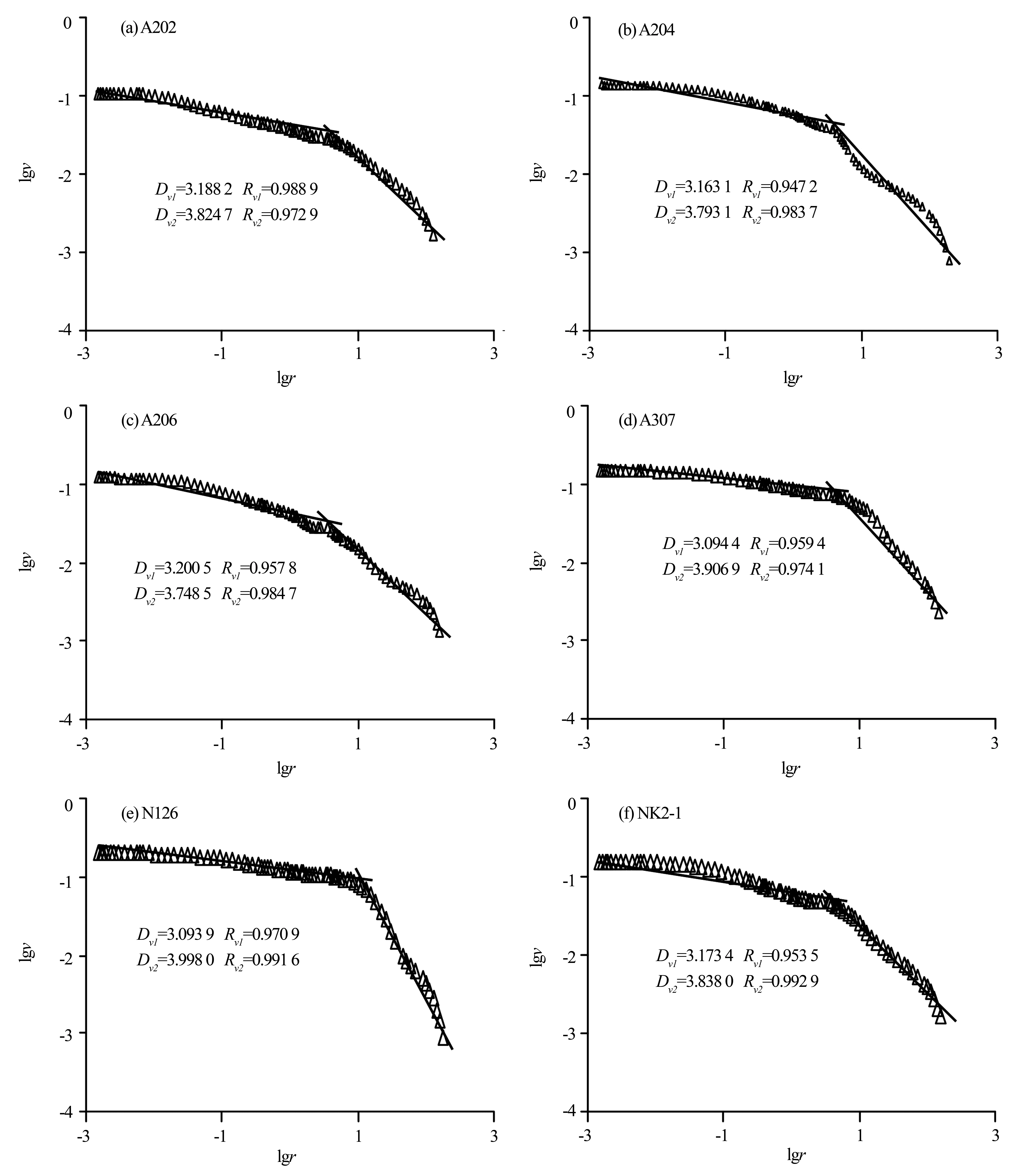
图2 lgr-lgv关系图

2.5 含矿层孔隙结构分形特征的成因

张宸恺等[3]的研究表明流体对不同孔径孔隙结构的改造程度存在差异可导致砂岩孔隙结构具多重分形特征。对于大孔隙，由于毛细管压力较小，流体易进入，流体对大孔隙结构的影响相对较大，可导致其复杂程度增加，具较高的分维值；而在小孔隙区，毛细管压力较大，流体不易进入，流体对小孔隙结构的改造作用相对较弱，分维值较低。因而认为流体对不同孔径孔隙结构的改造程度存在差异可能是导致本砂岩铀矿含矿层孔隙结构具双分形特征的一个重要因素。

3 结 论

含矿层平均孔径在68.8～225.9 nm之间变化，均值为144.6 nm，平均孔径总体较小。孔隙度变化于21.54%～34.92%之间，均值为27.30%。空隙总面积在2.581～6.275 m2/g之间波动，均值为4.357 m2/g。中值体积孔径的变化范围为304.6～9 178.5 nm，均值为3 252.3 nm。中值面积孔径在19.4～31.4 nm之间变化，均值为24.7 nm。根据汞饱和度与毛细管压力计算方法，大孔隙结构分维值在2.717 5～2.998 0之间变化，均值为2.820 5，小孔隙结构分维值在2.089 9～2.190 8之间波动，均值为2.146 6。依据孔隙累积体积与孔径计算方法，大孔隙结构分维值在3.748 5～3.998 0之间变化，均值为3.851 5，小孔隙结构分维值变化于3.093 9～3.200 5之间，均值为3.152 3。含矿层孔隙结构总体上具类似的分形特征和形成机理。大孔隙结构的分维值明显大于小孔隙结构的分维值，表明大孔隙结构的复杂程度明显大于小孔隙结构的复杂程度。含矿层孔隙度随大孔隙结构分维值的增加而升高，随小孔隙结构分维值的升高而降低。大孔隙结构的分维值可判定含矿层的渗透性，并且其高值指示渗透性低，而小孔隙结构的分维值不能判定含矿层的渗透性。流体对不同孔径孔隙结构的改造程度存在差异可能是导致本砂岩铀矿含矿层孔隙结构具双分形特征的一个重要因素。

参考文献：

[1] 张婷, 徐守余, 杨珂. 储层微观孔隙结构分形维数应用 [J]. 大庆石油学院学报, 2010, 34 (3) : 44-47.

[2] 李中锋, 何顺利, 杨文新. 砂岩储层孔隙结构分形特征描述 [J]. 成都理工大学学报：自然科学版, 2006, 33 (2) : 203-208.

[3] 张宸恺, 沈金松, 樊震. 应用分形理论研究鄂尔多斯MHM油田低孔渗储层孔隙结构 [J]. 石油与天然气地质, 2007, 28 (1): 110-115.

[4] 文慧俭, 闫林, 姜福聪, 等. 低孔低渗储层孔隙结构分形特征 [J]. 大庆石油学院学报, 2007, 31 (1): 15-18.

[5] SCHLUETER E M, ZIMMERMAN R W, WITHERSPOON P A, et al. The fractal dimension of pores in sedimentary rocks and its influence on permeability [J]. Fractals in Engineering Geology, 1997, 48: 199-215.

[6] RADLINSKI A P, IOANNIDIS M A, HINDE A L, et al. Angstrom-to-millimeter characterization of sedimentary rock microstructure [J]. Journal of Colloid and Interface Science, 2004, 274 (2): 607-612.

[7] TSAKIROGLOU C D, PAYATAKES A C. Characterization of the porestructure of reservoir rocks with the aid of serial sectioning analysis, mercury porosimetry and network simulation [J]. Advances in Water Resources, 2000, 23 (7): 773-789.

[8] 张金带, 徐高中, 林锦荣, 等. 中国北方6种新的砂岩型铀矿对铀资源潜力的提示 [J]. 中国地质,2010, 37 (5): 1434-1449.

[9] 李开文. 论我国地浸采铀技术的重大突破—新疆地浸采铀矿床的成功应用 [J]. 中国矿业, 2005, 14 (3): 1-8.

[10] 王海峰, 阙为明, 钟平汝, 等. 原地浸出采铀技术与实践 [M]. 北京: 原子能出版社, 1998: 1-182.

[11] 申维. 分形求和法及其在地球化学数据分组中的应用 [J]. 物探化探计算技术, 2007, 29 (2): 134-137.

[12] 陈程, 孙义梅. 砂岩孔隙结构分维及其应用 [J]. 沉积学报, 1996, 14 (4): 108-113.

[13] 江东, 王建华, 郑世书. 多孔介质孔隙结构的分形维数：测试、解算与意义 [J]. 科技通报, 1999, 15 (6): 453-456.

[14] 蔺景龙, 刘爽, 赵海波. 基于分形理论预测砂岩储层渗透率 [J]. 大庆石油学院学报,2004,28(5):1-3.