基于轴辐网络模型的中欧集装箱航线优化*
2012-05-10吴旗韬张虹鸥叶玉瑶陈伟莲
吴旗韬, 张虹鸥, 叶玉瑶, 陈伟莲
(1.广东省科学院广州地理研究所,广东 广州 510070;2.中国科学院可持续发展研究中心,北京 10010;3.中国科学院地理科学与资源研究所,北京10010)
随着国际集装箱运输蓬勃发展,航运公司不断建造更大型船舶满足不断增长的跨洋集装箱运输需求,超过10 000TEU的集装箱船舶成为远洋航运的标准[1],未来大型集装箱船舶甚至达到18 000 TEU[2]。为获得更多利润,航运公司不断减少大型集装箱运输船停靠的港口数量,航运企业选择水深条件好,物流网络发达的港口作为枢纽港,从而实现规模效益和高效的转运效果[3-4]。
现代大型集装箱船舶航线上仅保留少数枢纽港,如新加坡,香港,鹿特丹等,在枢纽港通过小型运输船将货物运送到周边支线港[5],整个航运网络呈现轴辐网络(hub-and-spoke network)连接形态。轴辐网络的基本原理是,在网络中一些节点被作为传输枢纽,物流从出发地运输到枢纽,再通过枢纽传送到目的地,取代了从出发地到目的地的直接运输[6]。与传统的网络结构相比,轴辐网络配置简化网络结构,减少网络成本,对货物集中处理和分类使货物承运人实现规模经济[4, 7-11]。轴辐网络出现和应用也被称为继集装箱化和多式联运之后第三次技术革命[12]。
学者对远洋航线轴辐模型的研究不断深入,在最初建立的海运总运输成本模型基础上[13],不断改进使得模型更加符合实际,如考虑支线港之间的连接[14],考虑货物在港的装卸和陆上运输成本[5],考虑枢纽港和支线港之间的线路连接[15]等等。研究的区域重点还是欧美地区[1,17-18],近年来国内的研究也不断增加[19-21]。
本文以中欧36个集装箱港口为例,以最小化集装箱定期班轮运输总成本为目标,优化集装箱定期班轮航线中枢纽港的选择,位置以及集货港和枢纽港的配置,为航运企业确定航线提供理论参考,并探索轴辐网络在远洋海运网络中的应用。
1 研究方法
1.1 模型建立和求解
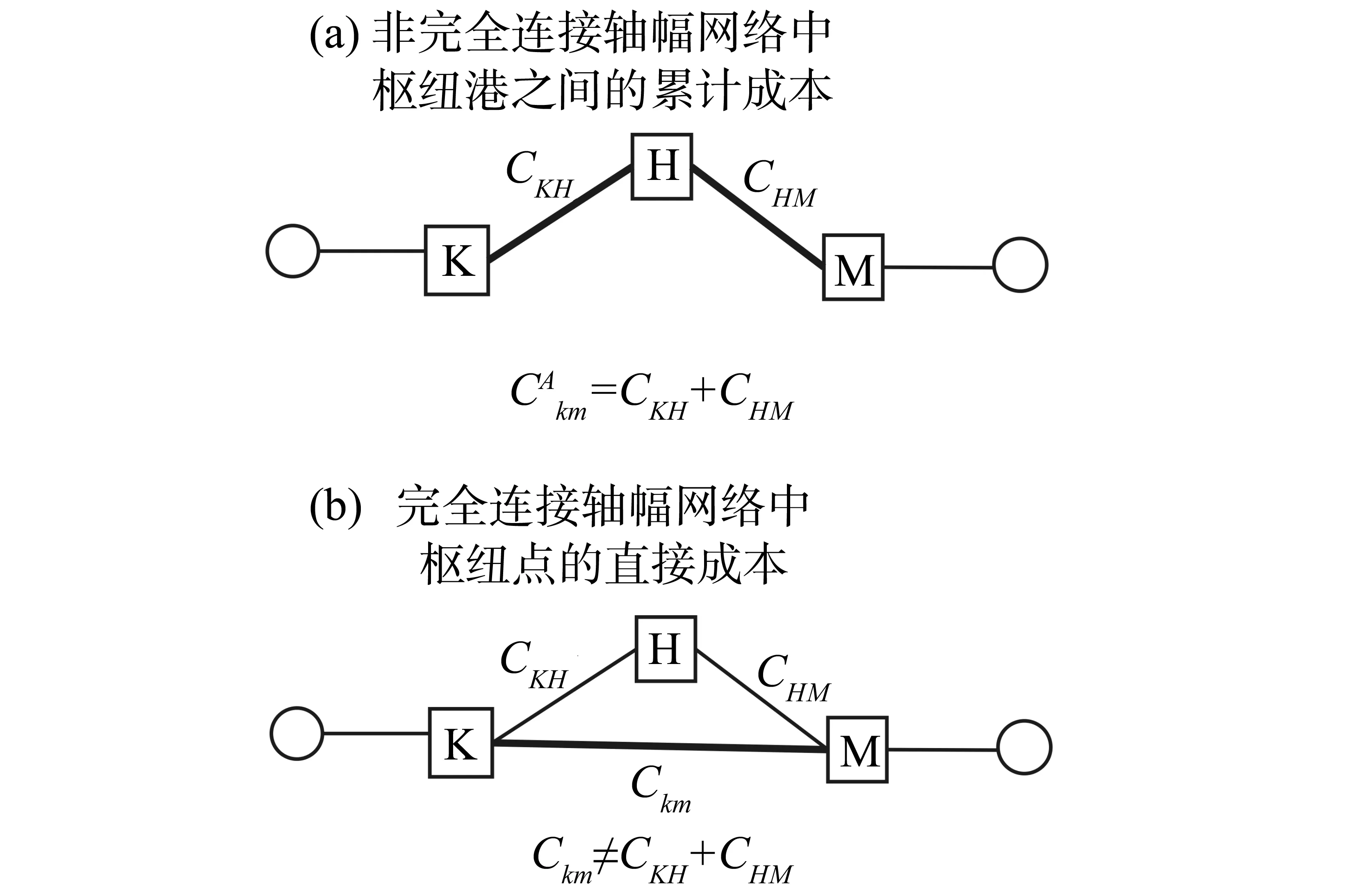
轴辐网络模型上个世纪80年代由O’Kelly建立,其理论模型较好地应用到航空领域[6, 9, 22-25]。但远洋航线网络和航空网络有一定的差别。首先远洋航线中,枢纽港之间不是完全连接的,船舶通常按照一定次序依次访问各枢纽港[13-14,26];其次,航空网络中,乘客通常按照原路返回,而远洋航运中,港口之间的运输是不平衡的,单一港口进港和出港的集装箱量差别较大,集装箱往往向一个方向输送。
本文在O’Kelly航空轴辐网络模型的基础上,建立海运轴辐网络模型,以描述远洋航运网络实际形态。在给定n个港口中,港口之间有不同的集装箱流量,选择p个枢纽港口,然后将非枢纽港口(集货港)配置到距离最近的枢纽港,使整个港口体系总运输成本最小化。轴辐网络研究问题具有多种类型,本文假设枢纽港和集货港,以及枢纽港和枢纽港之间不存在容量限制,集货港仅和单个枢纽港相连,因此,本文研究的轴辐网络类型为非容量限制单配置枢纽中位问题。
首先定义Xik和Xkk如下:
则海运轴辐网络模型可以用公式表示如下:
目标方程
(1)
限制方程
≥0,对所有的k
(2)
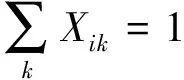
(3)
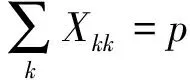
(4)
Xik∈{0,1},对所有的i,k
(5)
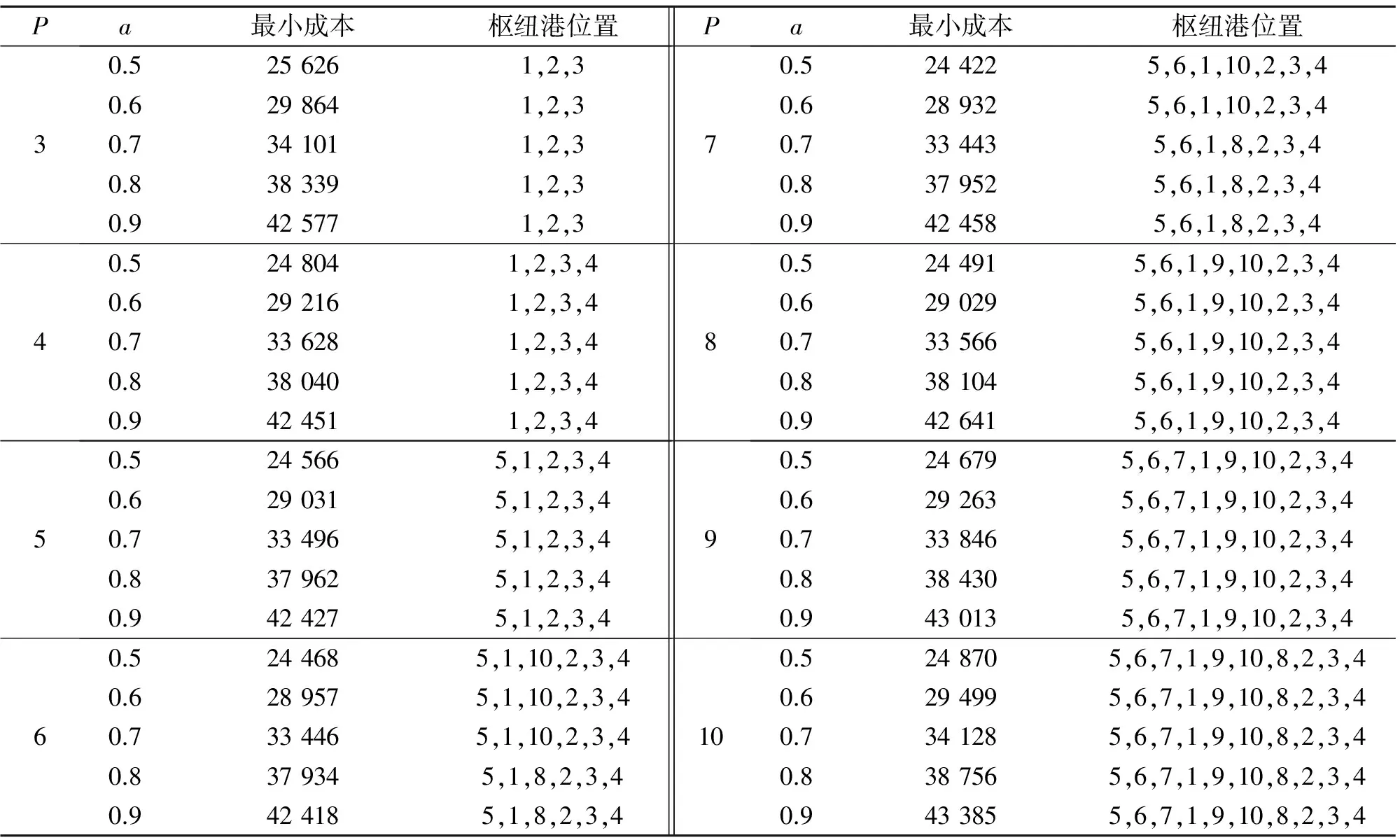
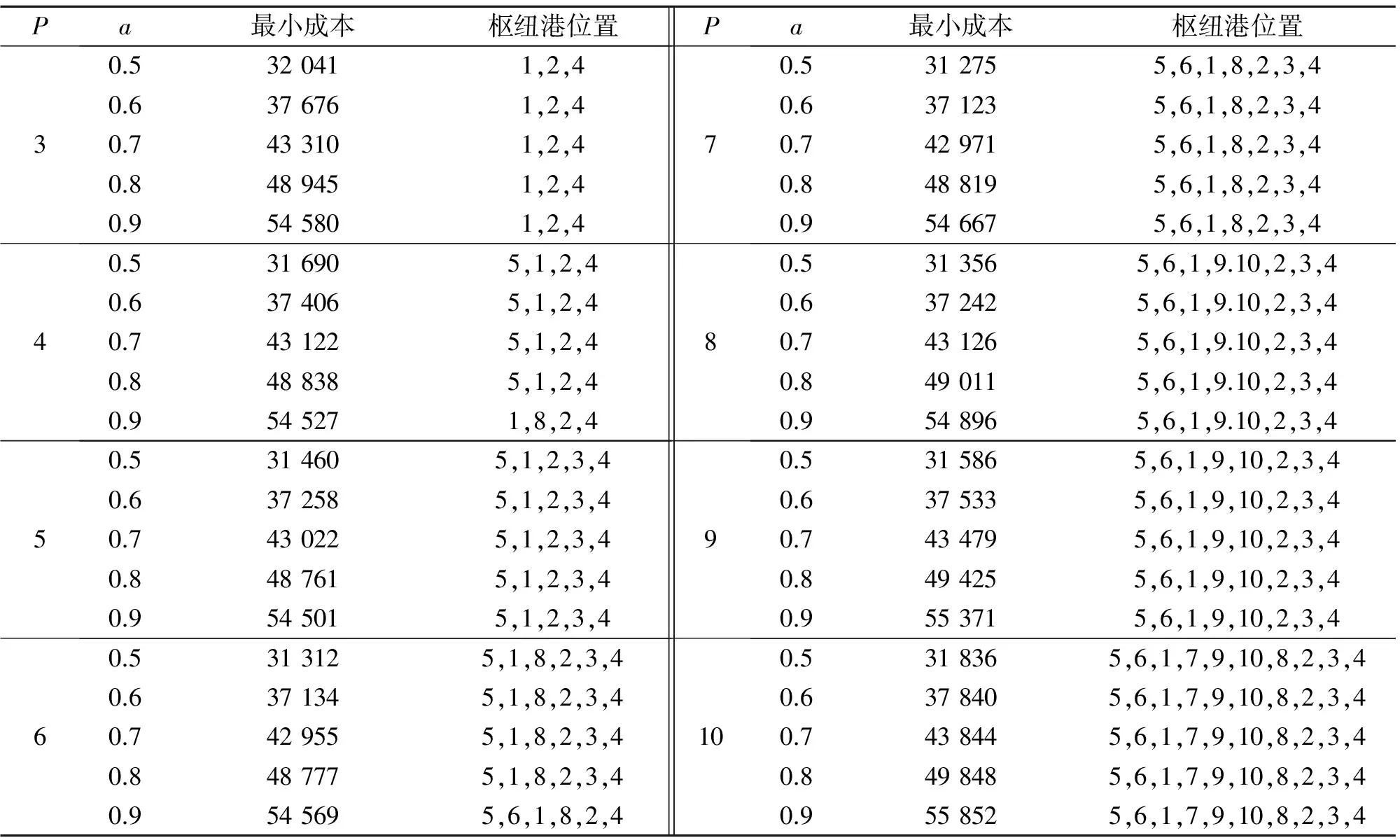
目标方程(1)计算了整个网络中的集装箱运输成本。总成本分为3个部分,依次分别计算起始地到枢纽港的成本,枢纽港到目的地的成本,以及枢纽港之间运输的成本。在公式(1)中a是折扣系数,是指枢纽节点之间每个集装箱运输成本和非枢纽节点与枢纽节点之间运输成本的比值。由于规模经济,使得枢纽节点之间的货运成本低于非枢纽节点到枢纽节点的成本,因此0 图1 依序累加与直航成本的比较 轴辐网络求解问题属于二次指派,由于优化方程具有非凹性,故无法保证所求的解为全局最佳解。本研究将采用O’Kelly所提出的启发式解法HEUR[22],不考虑以线性化的方法求解。具体方法为列举所有的轴心港组合,并在每一种轴心港中,指派集货港给距离最近的枢纽港,最后计算运输总成本,选择总成本最小的组合作为最优解。 本研究的原始数据源自欧盟统计局(Eurostat),为了减少数据分析的复杂性和不可获得性,本研究建立了非对称成比例模型来获得港口之间的集装箱运输O-D数据。模型假设单一港口与其他港口之间的运输量是不对称的,也就是说,港口的进口量和出口量是不相同的。其次,港口i从另一港口j的进口量与港口i从另一港口j所在国家进口量成正比,也与另一港口j向港口i所在国家的出口量占港口j所在国家总出口量的比例成正比,反之亦然。研究对每个港口进出口的集装箱量分别进行了计算,分别得到东向(西北欧-中国)和西向(中国-西北欧)集装箱运输数据。模型公式可以用方程(6)和(7)表示: (6) (7) 非对称成比例模型以现有港口向不同国家进出口的统计数据为基础,通过模型进行分解,得到港口对港口的运输数据,相对与其他的重力学模型[27-28]和货物转化模型[29],具有更高的有效性和可行性。 在全球三大集装箱东西运输航线中,亚欧航线是运输量最大也是最重要的的一条。中国的集装箱运输在近年来的发展突飞猛进,中欧之间的集装箱运输也呈现加速增长的趋势。研究区域选择中国和西北欧的共计36个集装箱港口。本研究以港口为单位而非港区,当地区具有多个港区时,将各港区集装箱吞吐量合并单一港口处理。港口分布方面,中国12个,西北欧24个。 相对传统点对点直线网络运输形式,轴辐网络具备规模经济性。运行模型进行模拟,在不同的折扣系数和不同的枢纽港个数情况下,选择不同折扣系数网络总成本最小值,结果表明轴辐网络总运输成本低于点对点直线网络(表1)。双向的总成本中,当折扣系数a为0.5时,总成本为55 709×106TEU·n mile,是传统直线网络总成本的53.64%,而折扣系数从0.5增加到0.9时,总成本分别为66 063×106,76 404×106,86 710×106和99 236×106TEU·n mile,都低于传统直线网络运输的总成本,成本节约率分别为63.61%,73.57%,83.49%,95.55%。在东向和西向航线的独立分析中,轴辐网络形态总成本也表现出相同的趋势,相对于传统网络总成本,轴辐网络总成本仅占53%~95%。 表1 轴辐网络和传统网络总成本对比 枢纽港个数的选择影响整个轴辐网络结构,也影响网络运输总成本。通过模型模拟,不同枢纽港个数情况下,网络运输总成本呈现“U”型变化(图2)。当枢纽港个数p增加时,运输总成本先减小然后再增加。以西向航线为例,当折扣系数为0.5和0.6时,在整个网络中设置7个枢纽港,可以使得运输总费用达到最小,增加或者减少枢纽港个数,运输总费用都会增加;当折扣系数为0.7时,在整个网络中设置6个枢纽港,运输总费用达到最小;当折扣系数0.8和0.9时,整个网络中只需设置5个枢纽港,运输总费用达到最小。东向航线中,折扣系数从0.5增加到0.7时,最小化运输成本时枢纽港设置的个数都为6个;折扣系数从0.8增加到0.9时,枢纽港设置的个数都为5个实现总成本最小化。对双向航线综合考虑,则折扣系数从0.5增加到0.6时,最小化运输成本,枢纽港设置的个数都为7个;折扣系数从0.7增加到0.9时,要实现总成本最小化,枢纽港设置的个数都为6个。 图2 不同枢纽港个数不同方向的总成本变化曲线 表2-4分别是东向,西向和双向航线中,枢纽港位置的模拟结果。在东西两个区域中,枢纽港的位置选择有一定的差别。在中国的枢纽港选择中,香港,高雄和上海成为不变的选择。在东向航线中,当模型中枢纽港设置为3个时,香港和高雄成为中国的枢纽港;而同样情况下,西向航线中,上海和香港则为枢纽港的最优位置;同样在双向航线中,上海和香港是最优化的枢纽港。而当模型中枢纽港设定为4个或者更多时,香港,高雄和上海则一直作为中国的最优化枢纽港选择。 而在西北欧,枢纽港的选择呈现多样性。当模型中枢纽港设定为3个时,西北欧的泽布吕赫港成为东向、西向和双向航线中的最优港;当枢纽港个数增加到4时,东向和双向航线中,无论折扣系数增减,选择泽布吕赫港和汉堡港都是最优解;而在西向航线中,当折扣系数为0.5~0.8时,泽布吕赫港汉堡港是最优解,当折扣系数升到0.9时,最优的枢纽港则变为勒阿弗尔港和泽布吕赫港。当枢纽港设置更多时,泽布吕赫港和汉堡港则一直作为西北欧枢纽港的最优选择,同时其他港口,如鹿特丹港, 安特卫普港, 费利克斯托港、勒阿弗尔港和南安普敦港也会成为枢纽港的选择。 不同方向的航线中,枢纽港的位置大致相同,但模型中设置的枢纽港个数为4和6个时,东西向航线和双向航线中,枢纽港位置会表现出一定的差别,如枢纽港个数为6个时,东向航线枢纽港组合为汉堡港,泽布吕赫港,南安普敦港,香港,高雄港和上海港,或者汉堡港,泽布吕赫港,勒阿弗尔港,香港,高雄港和上海港。而西向航线的枢纽港则为汉堡港,泽布吕赫港,勒阿弗尔港,香港,高雄港和上海港或者汉堡港,鹿特丹港,泽布吕赫港,勒阿弗尔港,香港和上海港。在双向航线中,最优化枢纽港组合为汉堡港,泽布吕赫港,勒阿弗尔港,香港,高雄港和上海港。 表2 东向航线枢纽港位置及最小化成本数1) 根据模型假设,枢纽港确定后,其他港口将被配置到最近的枢纽港,而且只能配置到一个枢纽,因此选择了枢纽港后,整个网络结构也就确定。以双向航线为例,当折扣系数为0.9,枢纽港个数为6时,整个集装箱网络结构如图3所示。汉堡港作为德国最大的集装箱港口,成为区域集装箱的枢纽港,不来梅港成为其集货港;比利时的泽布吕赫港则被配置了临近的荷兰,英国,比利时等国的港口;法国的勒阿弗尔港作为枢纽港,则周边爱尔兰,英国西部,法国的港口配置为其集货港;香港作为华南的枢纽港,深圳和广州配置成为集货港,高雄港被配置了台中港和基隆港,同时厦门港成为其集货港;位于长三角的上海港除了服务于本区域的宁波港外,还辐射到了环渤海的天津港,大连港和胶州半岛的青岛港。在其他的枢纽港个数选择情况下,集货港配置和网络结构将发生变化。 表3 西向航线枢纽港位置及最小化成本数 1) 表4 双向航线枢纽港位置及最小化成本数1) 图3 中国-西北欧集装箱航线配置 中国和西北欧之间的集装箱运输正呈现加速增长态势,这刺激航运企业投入更多资源争夺集装箱运输市场,更大型船舶用来作为国际集装箱定期班轮运载工具,从而实现规模经济。船舶大型化使得集装箱班轮只能停靠有限几个枢纽港,在枢纽港通过转运将货物运往支线港,航运网络呈现轴辐网络形态。本文以O’Kelly的航空轴辐网络模型为基础,依据海运特点,建立了海运轴辐网络模型,优化国际集装箱班轮航线网络。同时建立非对称成比例模型,来分解和计算不同港口之间的O-D数据作为模型计算的数据来源。最后选择中欧36个集装箱港口,优化集装箱定期班轮的航线网络。研究主要结论如下: 1)相对传统网络,轴辐网络明显减少港口体系的运输总成本,不同折扣系数条件下,轴辐网络的运输成本是传统运输网络形态总成本的53%~95%,表明了轴辐网络的经济效益。 2)在不同枢纽港个数条件下,轴辐网络总成本曲线呈现“U”字形,随着枢纽港个数的增加,网络总运输成本减小,当枢纽港个数达到特定值,网络总运输成本最小,然后随着枢纽港个数的增加网络总运输成本又呈现增加趋势。当枢纽港个数在6或7个时,网络总体运输成本实现最小化。 3)枢纽港位置在不同区域呈现不同变化。在中国,香港、高雄和上海是本区域最优的三个枢纽港,周边港口都被配置到这三个枢纽港中;而在西北欧,泽布吕赫港、汉堡港、鹿特丹港、安特卫普港、勒阿弗尔港、费利克斯托港、南安普敦港都可能成为区域的枢纽港,承担起区域集装箱的转运功能。 参考文献: [1] IMAI A, SHINTANI K, PAPADIMITRIOU S. Multi-port vs hub-and-spoke port calls by containerships[J]. Transportation Research Part E: Logistics and Transportation Review, 2009,45(5): 740-757. [2] WIJNOLST N. Ships, larger and larger: containerships of 18000 TEU: impacts on operators and ports[C]∥Proceedings of Dynamar Liner Shipping 2020 Workshop, London,2000:13-29. [3] SHIBASAKI R, IEDA H, WATANABE T. An international container shipping model in east asia and its transferability[J]. Research in Transportation Economics, 2005,13: 299-336. [4] NOTTEBOOM T E, RODRIGUE J P. Port regionalization: towards a new phase in port development[J]. Maritime Policy & Management, 2005,32(3): 297-313. [5] AVERSA R. A mixed integer programming model on the location of a hub port in the east coast of South America[J]. Maritime Economics & Logistics,2005,7: 1-18. [6] ALUMUR S, KARA BY. Network hub location problems: The state of the art[J]. European Journal of Operational Research, 2008,190(1): 1-21. [7] CHESTLER L. Overnight air express: spatial pattern, competition and the future in small package delivery services[J]. Transportation Quarterly, 1985,39: 59-71. [8] TOH R S, HIGGINS R G. The impact of hub and spoke network centralization and route monopoly on domestic airline profitability[J]. Transportation Journal, 1985,24(4): 16-27. [9] O′KELLY M E. The hub network design problem: a review and synthesis[J]. Journey of Transport Geography, 1994,2(1): 31-40. [10] DEVANY A S, GARGES E H. A forecast of air travel demand and airport and airway use in 1980[J]. Transportation Research, 1972,6:1-18. [11] KANAFANI A, GHOBRIAL A A. Airline hubbing: Some implications for airport economics[J]. Transportation Research Part A: Policy and Practice, 1985,19A(1): 15-27. [12] FOSCHI A D, CAZZANIGA FRANCESETTI D. The Impact of ‘Hub and Spokes’ Port Networks on Transport Systems[EB]. 2001-07-01. http:∥dx.doi.org/10.2139/ssrn.275156 [13] HSIEH S H, CHANG F R. Applications of the Hub-and-Spoke network model in routing liner ships[J]. Transport Planning Journal, 2001, 30: 871-890. [14] YU C C. A Marine Hub-and-Spoke Network Model that Permits Feeder Ports not to Connect to Hub Ports Directly[D]. Taiwan :National Chiao Tung University,2001:68. [15] KARLAFTIS M G, KEPAPTSOGLOU K, SAMBRACOS E. Containership routing with time deadlines and simultaneous deliveries and pick-ups[J]. Transportation Research Part E: Logistics and Transportation Review, 2009,45(1): 210-221. [16] TAKANO K, ARAI M. A genetic algorithm for the hub-and-spoke problem applied to containerized cargo transport[J]. Journal of Marine Science and Technology, 2009,14(2): 256-274. [17] KONINGS R. Hub-and-spoke networks in container-on-barge transport[J]. Transportation Research Record, 2006(1963): 23-32. [18] BAIRD A J. Optimising the container transhipment hub location in northern Europe[J]. Journal of Transport Geography, 2006,14(3): 195-214. [19] 王成金, 金凤君. 中国海上集装箱运输的组织网络研究[J]. 地理科学, 2006, 26(4): 392-401 [20] 徐国平, 宗蓓华, 李文顺. 海上集装箱运输中轴辐式航线结构的经济性分析[J]. 管理工程学报, 2008,22(1): 53-57. [21] 徐骅, 金凤君, 王成金. 集装箱环球航线的枢纽区位优化[J]. 地理学报, 2008,63(6): 593-602. [22] O′KELLY M E. A quadratic integer program for the location of interacting hub facilities[J]. European Journal of Operational Research, 1987,32(3): 393-404. [23] O′KELLY M E. Hub facility location with fixed costs[J]. Regional Science, 1992,71(3): 293-306. [24] GOETZ A R, VOWLES T M. The good, the bad, and the ugly: 30 years of US airline deregulation[J]. Journal of Transport Geography, 2009,17(4): 251-263. [25] RODRIGUE J P, COMTOIS C, SLACK B. The Geography of Transport Systems[M]. 2nd ed. New York: Routledge, 2009: 352. [26] WONG H L. Analyses of Marine Hub-and-Spoke Network Models for Routing Containerships[D]. Taiwan National Chiao Tung University,2006. [27] LEVINE B, NOZICK L, JONES D. Estimating an origin-destination table for US imports of waterborne containerized freight[J]. Transportation Research Part E: Logistics and Transportation Review, 2009,45(4): 611-626. [28] LEVINE B, NOZICK L, JONES D. Estimating an origin-destination table for us exports of waterborne containerised freight[J]. Maritime Economics & Logistics, 2009,11(2): 137-155. [29] LUO M, GRIGALUNAS T A. A spatial-economic multimodal transportation simulation model for US coastal container ports[J]. Maritime Economics & Logistics, 2003,5(2): 158-178.
1.2 数据来源和处理
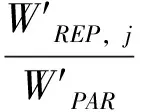

1.3 研究区域
2 模型结果
2.1 轴辐网络的规模经济性

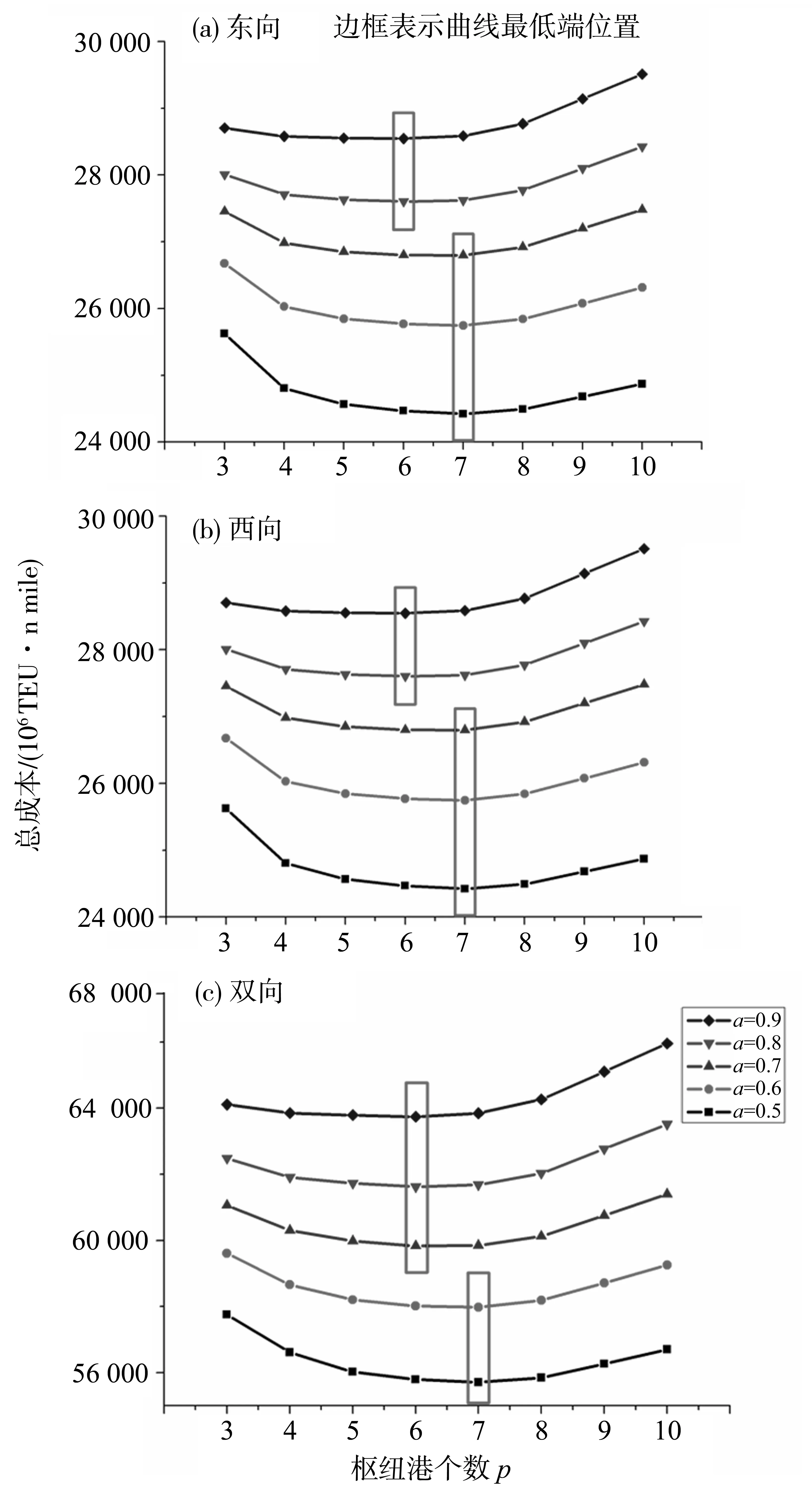
2.2 枢纽港个数优化
2.3 枢纽港位置选择


3 结 论
