压缩感知的自适应冗余字典及其图像恢复方法研究*

蒋业文,于昕梅

(佛山科学技术学院电子与信息工程学院，广东 佛山 528000)

压缩感知(CS，Compressed Sensing)的稀疏信号表示理论通常基于正交线性变换, 但许多信号是各种自然现象的混合体, 这些混合信号在单一的正交基变换中不能非常有效地表现出来。例如, 一个含有脉冲和正弦波形的混合信号, 既不能用单一的脉冲基函数, 也不能用单一的正弦基函数有效地表示。为此，CS理论采用一种新的信号稀疏表示技术，称为冗余字典，来表示这类混合信号。其基函数用称之为字典的超完备的冗余函数系统取代, 字典的选择尽可能好地符合被逼近信号的结构, 其构成可以没有任何限制, 字典中的元素被称为原子。从字典中通过测量矩阵找到具有最佳线性组合的m项原子来表示一个信号, 称作信号的稀疏逼近或高度非线性逼近。

CS理论的三个组成要素是信号的稀疏变换(目前的稀疏变换有离散余弦变换DCT,小波Wavelet，Curvelet，过完备原子分解(Overcomplete atom Decomposition)等)；稀疏信号的非相干测量及稀疏信号的重建算法[1]。CS主要思想是对一类具有稀疏先验的信号，先经小部分非线性测量矩阵进行采样，其包含足够信息良好逼近信号，再通过一定类型的线性或非线性解码机制就可高概率精确重建原始信号。信号稀疏表示的一个关键问题就是如何设计有效的冗余字典[2]。当前已有小波包、小波和正弦函数的级联、局部余弦等多种冗余字典，但它们不总能保证信号的稀疏性[3]。文献[4]选取可分离Gabor函数作为语音原子库，但离散Gabor函数中多个时频参数所得的原子数量巨大，增加了复杂度。近两年，通过学习、训练来获得冗余字典的方法也得到了发展，如文献[5]将聚类法用于图像字典学习；Aharon等[6]将K均值聚类法推广为K-SVD，自适应更新字典。但这些方法需通过训练大量样本来更新字典，计算量和存储空间巨大。

本文在研究稀疏表示的基础上，力图通过研究冗余字典寻找图像的一种最有效的稀疏表示及其重构图像的算法。

1 相关知识

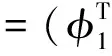
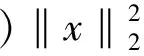
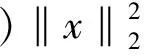
(1)

而对于全局RIP常数则为

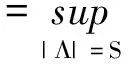
(2)

基于上述理论及其条件，本文主要解决的问题是，当信号不能用正交基稀疏表示时，采用冗余字典D∈Rn×k表示，并在满足RIP要求下如何选择合适的测量矩阵Φ∈Rn×d使传感系统矩阵ΦΨT具有更少的非零值[11]，同时运用迭代阈值算法概率恢复原始的信号。也就是说，如何从字典中D中找到具有最佳线性组合的m项原子来表示一个信号, 实现信号的稀疏逼近或高度非线性逼近。

2 冗余字典的构造

从非线性逼近的角度来讲, 高度非线性逼近包含两个层面: 一是根据目标函数从一个给定的基库中挑选好的或最好的基; 二是从这个好的基中拣选最好的m项组合。利用贪婪算法和凸优化自适应追踪, 从一个冗余函数系统中进行m项逼近或阈值逼近也属此例。下面我们从非相干字典与RIP界定方法出发，研究冗余字典的构造问题。

2.1 非相干字典

要想在冗余字典中获得高度非线性逼近的建设性结果, 我们必须首先将注意力集中在某些特别的字典上[12]。许多研究人员瞄准了非相干字典, 也就是说相干系数μ小于某个常数的字典。相干系数的定义为

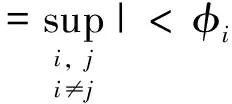
(3)

当相干系数较大时, 原子间的相互关联也较强。如果μ= 1, 则意味着字典中至少包含了两个一模一样的原子。反之, 当相干系数较小时, 我们就称字典是非相干的, 正交基的相干系数为零。相干系数为字典的冗余性提供了另一种可能的测度手段。(3)式说明当μ充分小时, 字典D(虽然可能是超完备的)接近一个正交基。

2.2 RIP界定问题

为了实现最佳的逼近并重构稀疏信号，Candes和Tao给出并证明了传感矩阵ΦΨT必须满足限制等容性条件RIP[2]。Baraniuk在文献[13]中给出RIP的等价条件是测量矩阵Φ和稀疏表示的基Ψ不相关, 即要求Φ的行φj不能由Ψ的列ψi稀疏表示, 且Ψ的列ψi不能由Φ的行φj稀疏表示。满足RIP条件的测量矩阵有高斯随机矩阵、贝努利矩阵、一致球测量矩阵、二值随机矩阵、局部哈达玛矩阵以及托普利兹(Toeplitz)矩阵等。对于大小为n×d的随机矩阵Φ，其满足的条件是[14]：

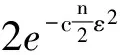
ε∈(0,1/3)

(4)

其中，P表示Φ满足的条件概率，ε为信号的残差。常数c>0，任意υ∈Rd。设D∈Rd×K为大小为K的字典，具有限制性等容常数δS(D),S∈N。对于满足(4)式的随机测量矩阵Φ∈Rn×d，当测量次数为[15]

n≥Cδ-2(Slog(K/S)+log(2e(1+12/δ))+t),

常数C≤9/c,δ∈(0,1),t>0

(5)

则传感系统矩阵ΦD具有限制等容性常数：

δS(ΦD)≤δS(D)+δ(1+δS(D))

(6)

对于固定的δ和计数器t，测量次数可以更精确地通过字典大小K和稀疏度S表示为

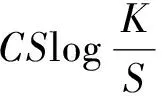
(7)

2.3 正交DCT基冗余字典

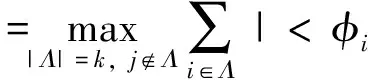
δS≤μ1(S-1)≤(S-1)μ

(8)

2.4 规范正交基(Dirac基)和DCT基组成的自适应冗余字典

通常一种正交基只能对某一种类型信号的特征存在稀疏表示。为此，本文根据规范正交基(Dirac基)和DCT基的表示性质，结合两个正交基组成一种组合变换稀疏表示方法，并通过Dirac基和DCT基构成自适应字典，实现信号的稀疏表示。

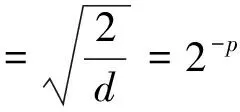
n≥C1(4S(2plog 2-logS)+C2+t)

(9)

如果信号仅在Dirac(Canonical Basis)基下稀疏，则测量次数为：

(10)

据此，利用Dirac基和DCT基构成自适应字典算法如下：

1)求出Dirac基向量在DCT正交基的展开系数(即基向量之间的内积)；求出S在两个正交基的展开系数(S与基向量的内积)并确定绝对值最大的基向量作为匹配原子。

2)利用Dirac基向量在DCT正交基的展开系数快速确定残余信号在各正交基中的展开系数，并确定其绝对值最大的基向量作为匹配原子。

以此类推得到S的稀疏表示。

2.5 基于图像分块的自适应冗余字典

为了说明本文提出的冗余字典有效性，我们以图像采样与重构作为输入条件，在不影响重构图像质量的前提下降低采样率，提出了分块自适应采样的方法。首先利用高斯随机投影矩阵对图像块进行随机投影，再根据观测向量的能量大小将观测向量分为平滑和非平滑两部分。由于平滑图像块和非平滑图像块的结构特征不同，因此本文对平滑块和非平滑块重构时选用不同的字典。将自然图像库中的图像块按其方向性从0°到180°共分为12类，每类数据分别用K-SVD(K-SingularValueDecomposition)方法训练一类字典，每类字典包括64个原子，另外再加上正交DCT字典一共形成包括832个原子的冗余字典。正交DCT字典可以表示图像块中的各向同性特征，而规范正交基字典可以表示图像中的角度，因此，我们用规范正交基冗余字典对非平滑图像块进行重构。平滑图像块的结构特征比较简单，用正交DCT字典就可以表示它的各向同性特征，因此对平滑图像块重构时使用正交DCT字典。

图1 正交DCT和自适应冗余字典原子,字典原子大小为8*8

3 实验结果

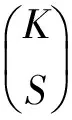
图2 基于DCT字典和自适应冗余字典的图像处理(Ⅰ)

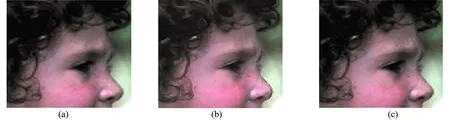
图3 基于DCT字典和自适应冗余字典的图像处理(Ⅱ)

由图2、3可见，在充分测量次数下，两种字典算法均可高概率恢复信号。但在测量次数一定时，由重构图像的峰值信噪比(PSNR)可见，本文提出的Dirac基和DCT基组成的自适应冗余字典具有更好的图像恢复效果。

5 总结和展望

通过分析CS理论信号的稀疏性和RIP条件，深入研究了一个正交DCT基以及Dirac基和DCT基构成的组合基冗余字典，确定了随机测量矩阵对信号测量次数的要求，以及测量次数与字典大小、信号稀疏度的关系。在此基础上，通过对图像按照能量进行分块，并结合迭代硬阈值重构算法，提出了一种自适应冗余字典的实现应用方法。实验结果证明了自适应冗余字典的有效性。我们进一步地研究方向是，结合冗余字典，寻找更优的测量矩阵，发展更有效和低复杂度的图像/视频压缩感知系统及其信号的重构算法。

参考文献：

[1] DONOHO D．Compressed sensing[J]．IEEEE Trans Inform Theory，2006，51(4)：1289-1306．

[2] CANDES E，ROMBERG J，TAO T．Robust uncertainty principles：Exact signal reconstruction from highly incomplete frequency information[J]．IEEE Trans Inform ，2006，52(2)：489-509．

[3] 孙玉宝, 肖亮. 基于Gabor感知多成份字典的图像稀疏表示算法研究[J]. 自动化学报, 2008, 34(11): 1379-1386.

[4] 井爱雯, 刘云. 基于MP算法的语音信号稀疏分解[J]. 计算机工程与应用, 2009, 45(5): 144-146.

[5] RUBINSTEIN R，ELAD M. Double sparsity: learning sparse dictionaries for sparse signal approximation[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1553-1564.

[6] AHARON M, ELAD M,BRUCKSTEIN A M. The K-SVD: an algorithm for designing of overcomplete dictionaries forsparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322.

[7] RUDELSON M, VERSHYNIN R. Sparse reconstruction by convex relaxation: Fourier and Gaussian measurements[C]∥Proc CISS 2006 (40th Annual Conference on Information Sciences and Systems), 2006.

[8] KIM S J，KOH K，LUSTIG M，et al．A interiorpoint method for large-scale L1-regularized least-squares problems with applications in signal processing and statistics[J]．Journal of Machine Learning Research，2007，7(8)：1519-1555．

[9] TROPP J，GILBERT A．Signal recovery from random measurements via orthogonal matching pursuit[J]．IEEE Tram Inform Theory，2007，53(12)：4655-4666．

[10] 杨海蓉，张成，丁大为，等. 压缩传感理论与重构算法[J].电子学报，2011，39(1)：142-148.

[11] RAUHUT H, SCHNASS K, VANDERGHEYNST P. Compressed sensing and redundant dictionaries[J]. IEEE Transactions on Information Theory, 2008, 54(5): 2210-2219.

[12] CHEN S, DONOHO D, SAUNDERS M. Atomic decomposition by basis pursuit[J]. SIAMJ Science Computer, 1999, 20: 33～61.

[13] BARANIUK R G. Compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118-121.

[14] NEEDELL D，VERSHYNIN R．Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[J]．Found Comput Math, 2009，9(3)：317-334．

[15] 赵慧民，郭一缜,丁晓艳，等.用于视频多播传输的压缩传感实现方法研究[J].中山大学学报：自然科学版,2012,51(1): 45-49.

[16] 练秋生，周婷. 结合字典稀疏表示和非局部相似性的自适应压缩成像算法[J].电子学报，2012，40(7): 1416-1422.

[17] BLUMENSATH T, DAVIES M E. Iterative thresholding for sparse approximations[J]. Journal of Fourier Analysis and Applications, 2008, 14(5/6): 629-654.