空间形式中平均曲率与纯量曲率成线性关系的紧致闭子流形*

王 琪

(贵阳学院数学系，贵州 贵阳 550005 )

文[1]首先研究了正曲率空间形式中紧致闭子流形为全脐或有全脐乘积分解的一种充分条件。随后，文[2-3]也对此作了研究。近来，文[4]给出的下列定理1，改进了文[1-2]的结论。

本文进一步得到如下定理A 。定理A推广并改进了定理1。

定理1[4]设Mn是空间形式Sn+p(1)中紧致的闭子流形且单位平均曲率向量在法丛中平行。若Mn有常数纯量曲率R而且

R>n(n-1)

则有如下结论：

(i)n≥8,p≥1时，或者n≥3,p≤2时，如果Mn的第二基本型模长平方S满足

那么或者Mn=Sn⊂Sn+p(1)，或者Mn=Sn-1×S1⊂Sn+1(1)⊂Sn+p(1)。

定理A 设Mn是空间形式Sn+p(1)中紧致的闭子流形且单位平均曲率向量在法丛中平行。设Mn的纯量曲率R与平均曲率H在Mn上成一般线性关系aR+bH=c，其中a,b,c为常数且a,b不同时为零，又当a≠0时要求

≥n(n-1)

则也有定理1中的结论(i)、(ii)和(iii)。

1 准备知识和若干引理

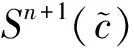
1≤i,j,k,l,m≤n,n+1≤α,β,γ≤n+p

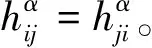
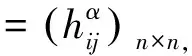
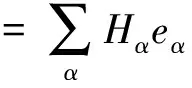
Mn的黎曼曲率张量Rijkl，法曲率张量Rαβij及纯量曲率R有如下关系(文[1-2])

,

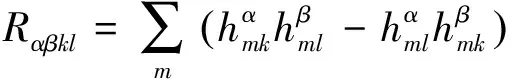
(1)

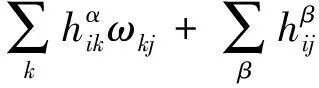
(2)

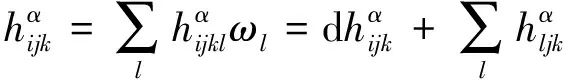
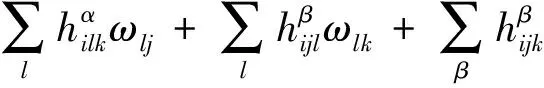
(3)

且有下列关系

,

(4)

而且有

Δα,

(5)

我们需要考虑Mn上二阶微分算子◇如下(文[1-3，5])

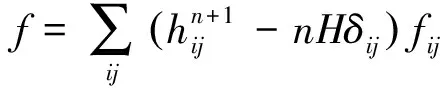
(6)

其中fij是f在Mn上的二阶协变微分。

,

本文需要用如下几个基本引理。

≤,

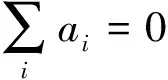
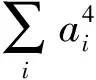
引理2[6,8]设An+1,…,An+p是p个n×n矩阵。写

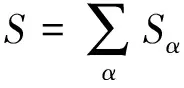
则有

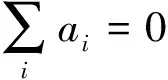
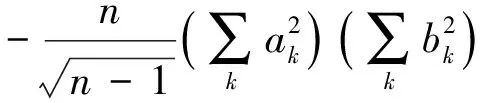
引理4 当n≥3时，有

证明首先由Schwartz不等式有

再由公式(5)和引理3即得。

引理5 当n≥2且p≥1时，有

将引理2和引理3用于上式即得。

引理6 当n≥8时，或当n≥3且p≤2时，有

证明p≤2意味着诸Lα可以同时对角化，由此易得。

引理7 当您n=2,p≥1时，有

证明 当n=2时，引理5的不等式右边第4 项小括号中可以算出，即得。

(7)

并且有如下结论：

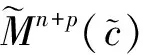
aR+bH=c

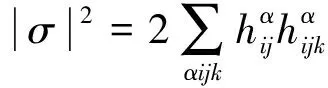
(8)

现在，(8)式两边取摸长平方并用Schwartz不等式，可得

(9)

从(9)式并注意aR+bH=c，就得

≥

(10)

2 定理A的证明

首先，(7)式两边取模长平方再用Schwartz不定式，得

(11)

由(10)式并注意aR+bH=c，得

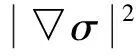
(12)

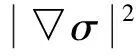
(13)

以下分几种情况讨论：

① 当n≥8,p≥1时，或当n≥3,p≤2时，由引理4和引理5得

ΔΔ

(14)

(15)

再由引理8知H>0在Mn上为常数，从而又由式(14)知只有两种可能，即

≡0或S≡

第一种情况说明SI≡0,Sn+1≡nH2并且有

Mn=Sn⊂Sn+1(1)⊂Sn+p(1)

② 当3≤n≤7时，由引理3和引理4得

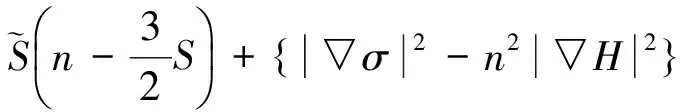
(16)

M2=S2⊂S3(1)⊂S2+p(1)

③ 当n=2,p=2时，由引理9得

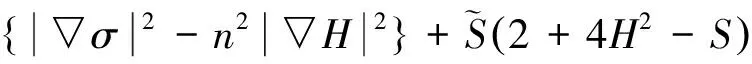
(17)

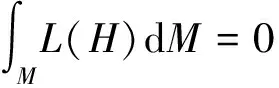
④ 当n=2,p≥3时，由引理6和引理7得

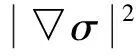
(18)

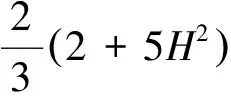
致谢作者衷心感谢编辑和审稿专家提出的极有价值的意见！

参考文献：

[1] YAU S T. Sub-manifolds with parallel mean curvature I, II [J]. Amer J Math, I, 1974, 96(2): 346-366; II, 1975, 97(1):76-100.

[2] SHEN Y B. Sub-manifolds with nonnegative sectional curvature [J]. China Ann Math, 1984, 5B (4):625-632.

[3] 林森春. 纯量曲率和平均曲率成线性关系的完备超曲面[J]. 数学年刊，1989, 10A(3): 333-344.

[4] ZHONG H H. Sub-manifolds of constant scalar curvature in a space form [J]. KYUNGPOOK Math J, 1998 (38):438-458.

[5] HONG W X. On closed minimal sub-manifolds in pinched Riemannian manifolds [J]. Transactions of the American mathematical society, 1995, 347(5): 1743-1751.

[6] LI A M, LI J M. An intrinsic rigidity theorem for minimal sub-manifolds in a sphere, Ark Math, 1992, 58: 582-594.

[7] LI H Z. Global rigidity theorems of hyper-surfaces [J]. Ark Math, 1997, 35: 327-351.

[8] SUNG EUN KOH. A characterization of round spheres [C]∥Proc Amer Math Soc, 1998, 126: 3657-3660.