基于0.18 µm CMOS的电流模单元最优化设计

郭杰荣,李长生,刘长青



基于0.18 µm CMOS的电流模单元最优化设计

郭杰荣,李长生,刘长青

(湖南文理学院 物理与电子科学学院, 湖南 常德, 415000)

采用HSPICE对基于0.18 µm工艺电流模单元进行了最优化分析. 以S2I存储单元为例, 进行了电路性能、参数扫描及蒙特卡洛分析, 对基准电源CMOS模型参数设定进行了最优化处理. 结果证明了该方法的有效性及电路可靠性.

电流模; 最优化; 蒙特卡罗

随着0.13～0.18 µm工艺的成熟, 第三代(Level 49) CMOS模型在设计仿真中的应用越来越广泛. 此类模型主要以缩减的物理性参数为主, 实验性参数为辅, 仿真模拟时具有更高的效率及收敛性[1]. 目前在处理该类模型的软件方面, HSPICE相对于其他电子电路仿真软件具有较强的优势, 主要体现在模型识别和仿真精度方面. HSPICE有着众多的模型, 以MOS管为例, HSPICE拥有从1到58级的MOS管模型, 而一般软件只能处理到第3级模型. 在CMOS模拟电路仿真时, 选用Level = 49的模型会比level = 3的模型更接近于实际电路[2]. 一般说来, 只要厂家给的SPICE模型是正确的, 用HSPICE仿真出来的结果与实验结果是符合得较好的. 另一方面, HSPICE可以直接对多种软件生成的网表进行仿真, 如Caelenee软件包的composer和Analog Ar- tist, Design Arelliroer以及WorkView都可以直接生成网表为HSPICE所用, 而不需要再进行一些非控制性的修改, 因而在网表的接口方面兼容性较强. 本文采用HSPICE对采用0.18 µm CMOS工艺的电流模单元进行性能分析与优化设计.

1 工艺模型及软件平台简介

1.1 0.18 µm CMOS 工艺模型

第三代(Level 49)CMOS模型以BSIM3、MOS MODEL 9 为代表, 是1995年由加州柏克莱分校推出的基于深亚微米MOSFET模型, 包含52个直流电流参数、10个工艺参数、15个电容参数、8个温度参数等100多个参数(不同版本略有不同). 模型考虑了阈值电压下降、均匀掺杂效应、垂直电场引起的迁移率下降, 载流子极限漂移速度引起的沟道电流饱和效应、沟道长度调制、漏源电源引起的表面势垒降低而使阈值电压下降的静电反馈效应、衬底电流引起的体效应、亚阈值导通效应、寄生电阻效应等. 而在HSPICE中, 为简化模型调用的复杂性, 对于源、漏极二极管电流、电容与电阻均使用与其他HSPICE中MOSFET相同的模型参数, 特别是对于Level 49模型可以参数化处理, 在模型中加入工艺参数的漂移, 这对于优化设计极为有利[1]. 以N_18_G2为例, 其模型参数(共112个)如下: .MODEL N_18_G2 NMOS + LEVEL = 49, LMIN = 1.8E-7, LMAX = 5.0E-5 + WMIN = 2.4E-7, WM- AX = 1.0E-4, TNOM=27.0…+XPART = 1, CF = 1.533E-10, ACM = 3 + HDIF = 2.6E-07, RSH = 8.

1.2 HSPICE性能及最优化分析方法

HSPICE除了具有通用电路仿真软件所有的基本特性外, 还具备了其他软件所没有的新特点[3]:

a. 优越的收敛性. 在早期的SPICE模型中, 由于实际元件的特性是连续的, 而很多电路的饱和区与线性区的工作点在两区交界点处并不连续, 故造成不收敛情况. 而在HSPICE中通过修正元件的模型、方程式及算法(algorithm)来改善算法求解时的收敛性软件中有多项设定选择, 所以有极好的收敛性.

b. 精确的模型参数，包括许多Foundry模型参数. 由于芯片制作过程的进步, 使得元件进入次微米或毫微米时代, 所以在电路模拟上对元件模型的精确性与应用有更严格的要求.

c. 极/零点分析. 此分析是HSPICE中特有的功能之一, 特别是对于网路分析与类比电路如放大器、滤波器等设计尤为重要. 通过分析极点、零点的分布, 可以分析系统的稳定度.

d. 参数化单元的输入、输出和行为代数化. 集成电路产品的性能好坏, 除了设计及制作过程外, 在产品的使用或可靠性的测试等都可以反应出产品的品质及合格率. 在HSPICE中, 可用蒙特卡罗统计分析, 用测试的结果来修正原来的设计规则; 同时还可以进行最坏情况分析(worst case)模拟, 以便提供产品性能的评估与合格率的分析.

而在HSPICE中对于任何元件或电路单元都可以参数化, 其输出、输入都可以用代数式来描述, 并做运算. 其基本参数化的例子如下说明:

.PARAM X=5(变数参数化, parameterization)

.PARAM X=‘Y+3’(代数运算, algebra)

而代数式运算也可当成输出, 如下所示:

.PRINT CGD=PAR(‘(X18(M1)+X19(M1))’)

另外, HSPICE还具有较高级逻辑模拟标准库的单元特性描述工具, 能对PCB、多芯片系统、封装以及IC技术中连线间的几何损耗加以模拟.

2 电流模式存储单元模型

基本的开关电流模块是一种电流采样电路. 目前广泛应用的有两种结构: 第1代T/H结构和第2代电流镜结构[4]. 第2代电流镜结构采用两步采样技术降低存储误差. 第1步输入电流存储在Mcoarse晶体管, 然后把存储在Mcoarse的误差提取出来存储在Mfine, 最后, 输出信号由两个晶体管输出而误差被抵消. 电路结构与时序如图1所示.

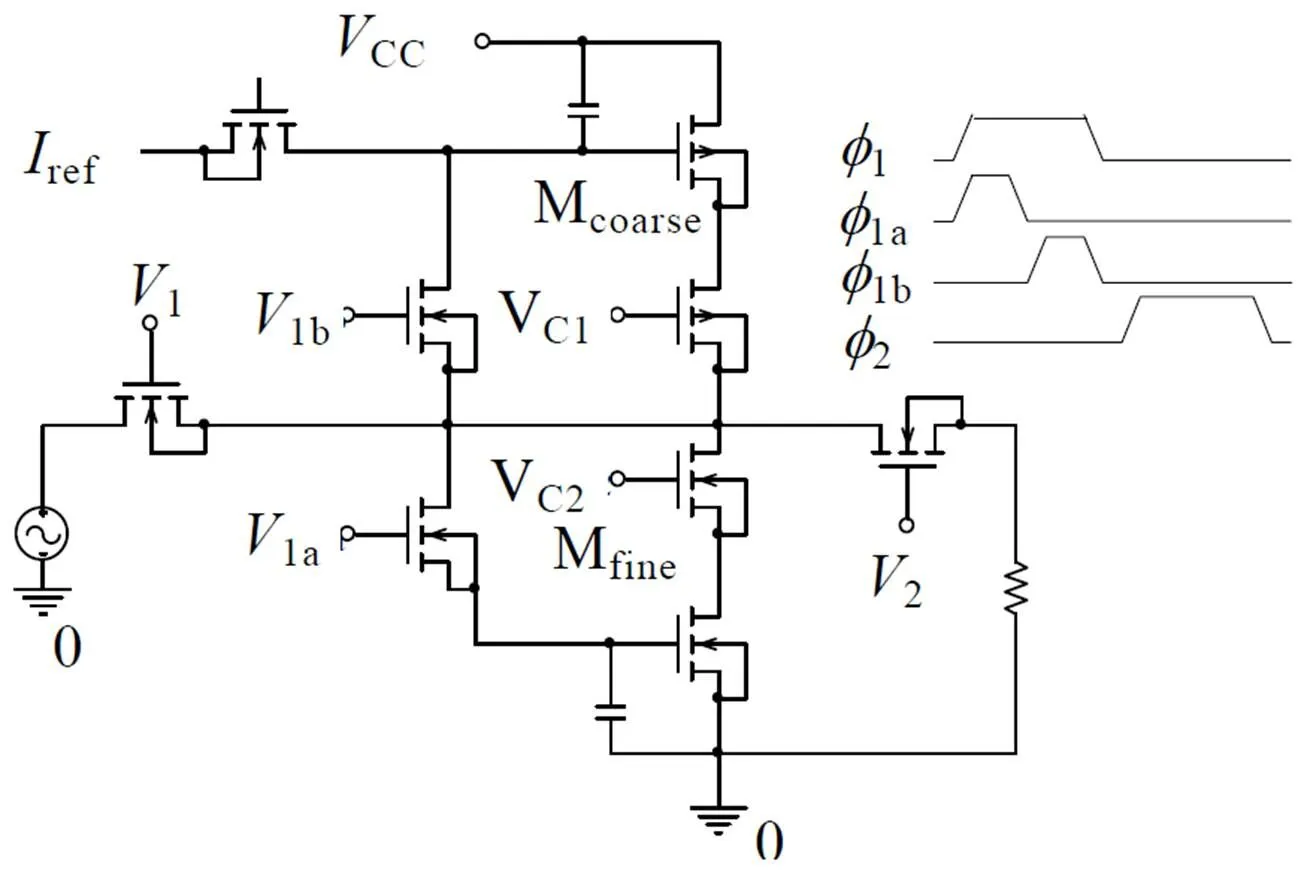
图1 第2 代电流镜结构及其工作时序

采样时序如下:

1: 采样.

1a: 采样保持输入电流in到Mcoarse存储晶体管,1a期间实际存储在Mcoarse的电流C=BIAS+in+i, 其中i是电荷注入与设置误差形成的误差;

1b:1a存储到Mcoarse同时将其连同参考电流BIAS到Mfine存储晶体管,1b期间实际存储在Mfine的电流f=BIAS+i;

2: 输出.out=BIAS+i-(in+BIAS+i)=-in

3 HSPICE仿真

3.1 HSPICE仿真基本流程

HSPICE仿真基本流程包括: 输入电路网表——确定元件参数及模型——确定仿真类型——仿真——输出结果分析.

HSPICE是一个在cmd shell窗口中运行的程序, 无图形化界面, 不具备绘图功能. HSPICE采用网表形式输入电路, 输入网单文件是一个有特定格式的纯文本文件, 可在任意的文本编辑工具中编辑. 设计者可以通过其他电路绘图软件绘制仿真电路图, 生成网络报表. HSPICE的输出也是一系列纯文本文件, 根据不同分析要求, 输出不同扩展名的文件. 如: .lis .mea .dat .smt等. HSPICE分析结果的浏览可在avanwaves中进行.

图1电路的CMOS晶体管仿真模型均采用0.18 µm工艺N_18_G2模型, 其沟道尺寸采用= 1.8-7= 10-7µm.

3.2 基本仿真结果

对电路采用瞬态仿真分析, 并绘制输入输出波形, 其功能语句如下:

.PRINT TRAN I(r_r2) I(I_I3)

.TRAN 0.1NS 0.3 µs

输出波形在avanwaves可进行分析与测量.

采用10 MHz, 100 mA正弦波信号作为输入信号, 参考直流信号为100 mA, 得到输入、出波形如图2所示.

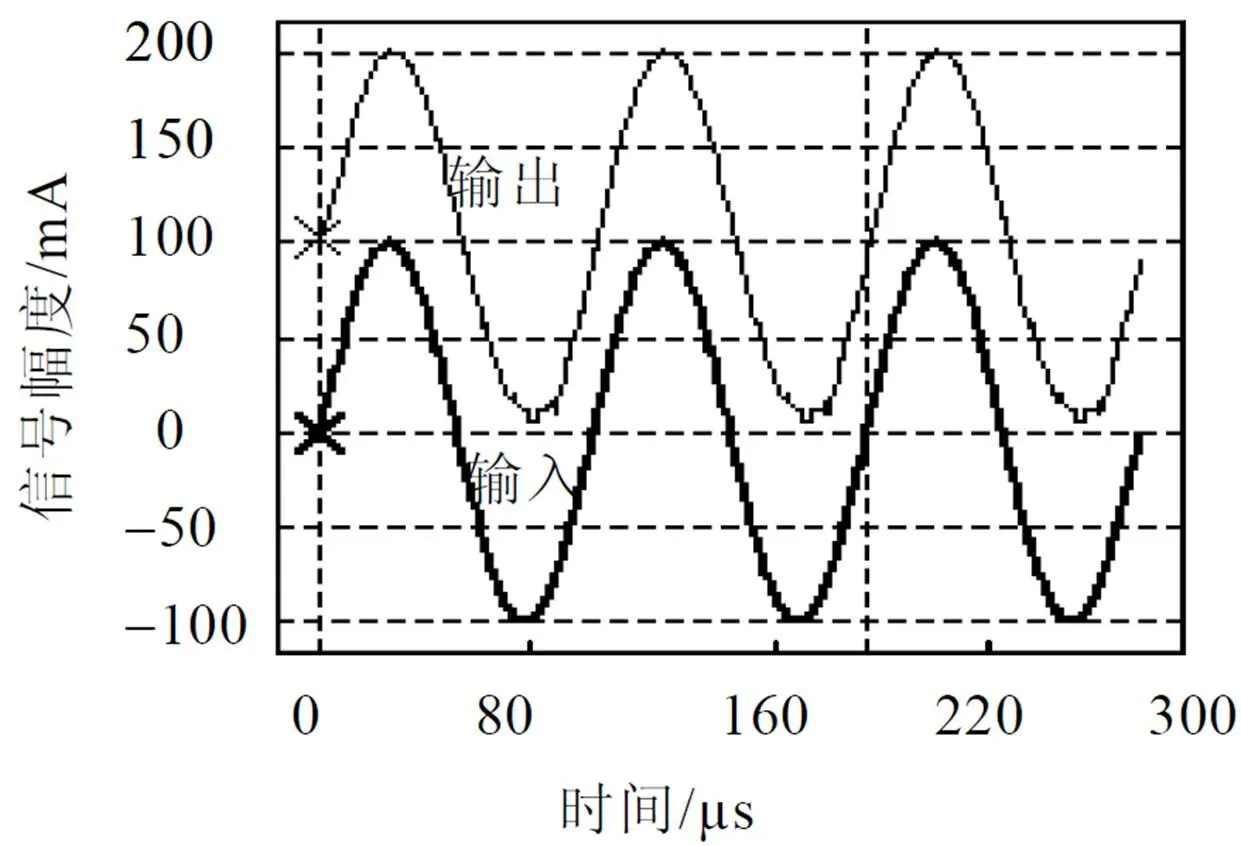
图2 输入、输基本波形

由图2可以看出: 输入输出波形基本一致, 由于晶体管开关电平的影响, 输出波形出现明显的开关寄生信号, 可通过适当提高参考电流加以改善.

4 模型参数扫描及最优化设计

在HSPICE中对于任何元件或电路单元都可以参数化, 其输出、输入都可以用代数式来描述, 并做运算. 这是其他仿真软件所不具备的功能.

4.1 参数扫描分析

根据设计需要, 首先要定义扫描的参数, 在电路中引用该参数; 同时给出参数取值列表, 在分析语句中加入DATA = datanam, 指定参数对应的数值表. 首先考虑参考电流变化对输出信号的影响, 确定扫描范围为80～150 mA, 输出信号结果见图3. 由图3可以看出, 参考电流对开关寄生信号有明显改善, 较为合适的电流为110 mA.

图3 参考电流源扫描分析结果

4.2 HSPICE 蒙特卡罗分析设定

在HSPICE中, 设定蒙特卡罗分析涵盖下列的叙述[5-6]:

a. 蒙特卡罗应用在直流操作点计算、直流扫描、交流扫描及暂态分析的次数决定于分析的关键字MONTE 的数值, 如下例: .TRAN 0.1NS 0.3uS sweep monte=120

上述设定描述直流扫描, 蒙特卡罗分析10次.

b. PARAM叙述. 其目的是设定一个合适的分布函数(高斯、均匀或随机极限分布)给一个模型或元件参数. 此功能允许参数化的电路原理图, 不需额外的修正即可做蒙特卡罗分析, 其基本格式如下:.PARAM XX = UNIF(Nom_value, Rel_variation, multiplier)

采用HSPICE对N_18_G2模型内部参数tox(标准值4.20000E-09)进行蒙特卡罗分析.由图4可以看出: 模型参数tox对电流镜像传输无明显影响.

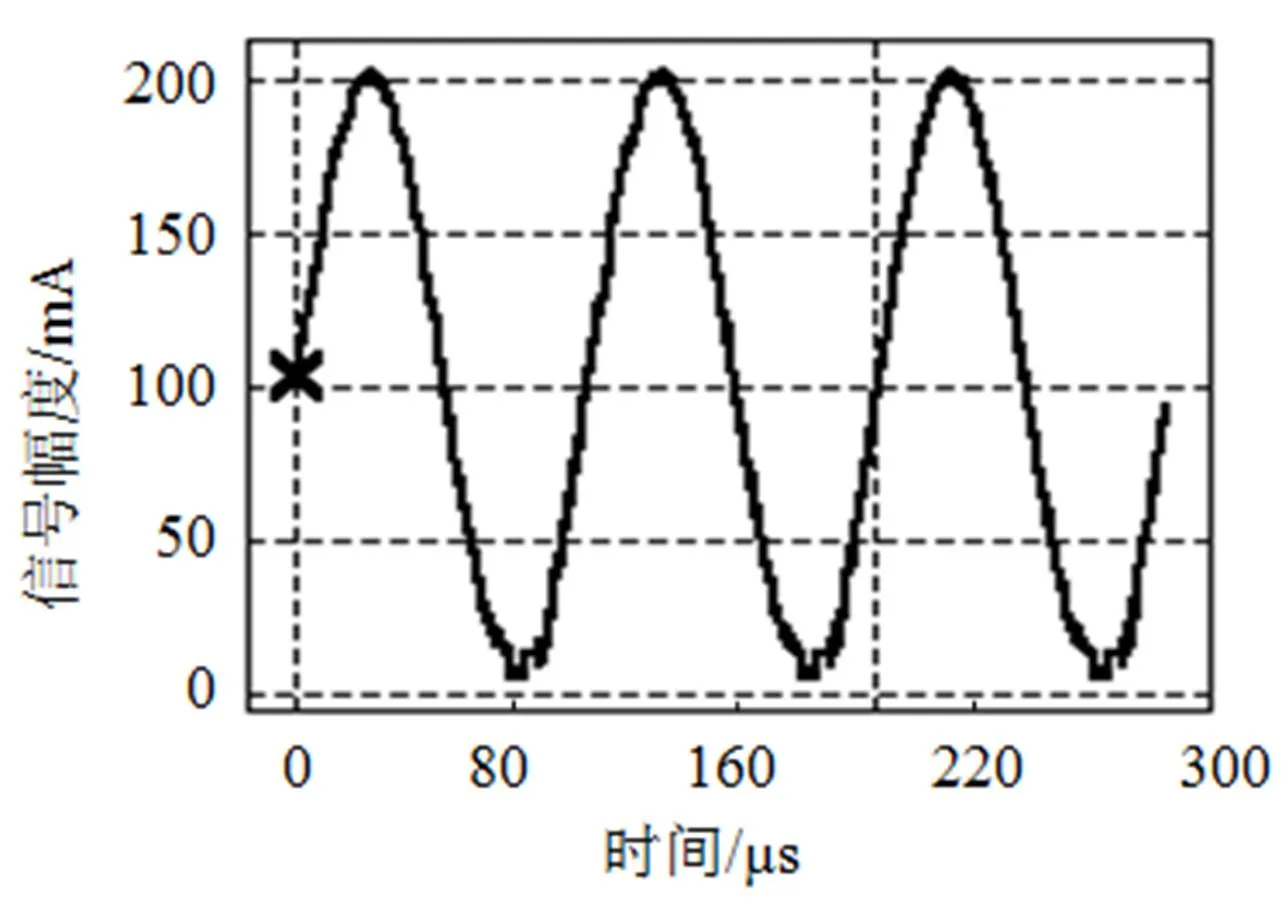
图4 模型参数tox蒙特卡罗扫描分析结果

5 结束语

本文采用HSPICE对0.18 µm CMOS的电流模单元内部参数进行蒙特卡罗分析的方法对电路进行最优化设计, 研究了参考电流优化与模型参数优化分析. 仿真结果验证了电路结构的有效性.

[1] 钟文耀, 郑美珠. CMOS电路模拟与设计——基于Hspice[M]. 北京: 科学出版社, 2007: 129-135.

[2] 陈苑锋, 曾晓萌, 何礼熊. HSPICE和PSPICE应用中的几个问题[J]. 福建电脑, 2002(4):13-14.

[3] Synop sys Inc. Star Hspice user guide[R]. Fremont, US, 2002: 1-3.

[4] Sinn P, Roberts MG W. A comparison of first and seco- nd-generation switched-current cells[J]. IEEE Internati- onal Symposium on Circuits and Systems. 1994(5): 301- 304.

[5] 汪汉新, 朱翠涛, 陈亚光. PSpice在电子电路优化设计中的应用[J]. 微计算机信息, 2006, 22(10-2): 111-113.

[6] 李慧贞. 基于蒙特-卡罗法的电子电路统计分析仿真[J].航空电子技术, 2005, 36(2): 33-37.

Optimization design on low-pass filter of channel transmission

GUO Jie-rong, LI Chang-sheng, LIU Chang-qing

(College of Physics And Electronics, Hunan University of Arts and Science, Changde 415000, China)

SI cell design used HSPICE are discussed in this paper. As an example, the sweep analysis on performance parameter of a S2I cell circuit are Implemented. Optimization processing of the structure and parameters are completed. And then the Monte Carlo method is using on the estimation of CMOS model parameter. The results prove the validity of this method and the reliability of the circuit.

current model; optimization; Monte Carlo

TN 306

1672-6146(2012)01-0039-03

10.3969/j.issn.1672-6146.2012.01.011

2011-11-07

国家自然科学基金项目(11104069); 湖南省科技计划项目(2010FJ4141); 湖南省重点建设学科“光学”基金.

郭杰荣(1973-), 男, 博士, 副教授, 研究方向为光电信息处理与光电子材料特性测试. E-mail: jierong_guo@yahoo.com.cn

(责任编校:刘刚毅)