采用分支理论对急冷过程中多定态现象的研究
2012-05-09张爱龙
张爱龙
采用分支理论对急冷过程中多定态现象的研究
张爱龙
(湖南文理学院 物理与电子科学学院, 湖南 常德, 415000)
通过一个简单模型模拟了合金Pd82Si18的急冷过程, 分析实验上难以测定的热传输指数对凝固过程中相关参数的影响. 结果显示, 当冷模温度足够慢地从900K下降到300K时, 对应2.0×105~5.0×105W/(m2K)范围内的热传输指数, 多定态现象发生. 当多定态发生, 冷模温度达到一个临界值时, 固液界面上会产生剧烈的温度下降. 随着该温度的突然下降, 在液固界面上很可能会发生玻璃转变.
急冷; 多定态; 玻璃转变
通过把金属熔体直接和冷模接触来实现快冷的方法已经被广泛应用于得到新的微观结构, 例如金属玻璃、纳米晶体等. 已经有大量的理论计算和模拟研究对快冷过程机理进行了探索[1-10]. 在急冷过程中[10], 当薄片和衬底之间具有良好热接触时, 很薄一层金属熔体突然与冷衬底接触, 熔体急速冷却, 液固界面上产生很大过冷并导致远离平衡. 考虑到系统远离平衡和急冷过程中的晶体生长动力学, 可以用非平衡动力学理论来研究熔体急冷过程. 在过去几十年里, 分支理论被广为采用来描述化学、生物中的非线性现象[11-13]. Creel等人[13]指出, 即使在一个简单的封闭系统中, 反应率与温度间的耦合也会导致多定态现象的发生. 不过, 分支理论很少被应用于物理系统. 近来曹标[14-15]等人提出一个理想快冷模型并应用分支理论研究玻璃转变.
本文在文献[14-15]的基础上, 提出一个更接近实际的合金Pd82Si18的急冷模型, 并用分支理论进一步研究快速凝固.
1 理论模型
单向凝固模型如图1所示, 在该模型中, 很薄一层合金Pd82Si18熔体突然与冷模接触, 从熔点温度m开始快冷. 冷模温度0则缓慢地从900 K降低到300 K. 冷模与薄片间的热传输可以假定为Newtonian方式. 不过, 需要指出的是, 在很多快冷过程中都发现, 尽管处于Newtonian冷却条件下, 液体中仍然有很大的温度梯度[16]. 在本文的简单模型中, 假定固体中不存在温度梯度, 液体中则存在正的温度梯度; 薄片很宽但很薄, 平行于液固界面的热传导可以忽略, 系统可以作为一维体系来进行研究. 在快冷过程中, 热量通过固体部分传到冷模, 而液固界面向相反方向移动, 在图1中用晶体生长率来表示. 熔体其它表面则假定是不传热的.

图1 合金Pd82Si18 的单向凝固模型以及温度分布, q 代表热流, u 代表晶体生长率
在本研究中, 固体作为一个开放系统来处理, 质量和能量流流过液固界面和固体—冷模界面. 对于给定冷模温度, 热平衡方程可以写为:

其中是液固界面位置,s是固体密度,ps是固体比热,是固体温度,L是液体温度,是热传导, Δm是熔化热,是热传输指数. 晶体生长率可以写为[17]:

其中B是Boltzman常数,0是散射分子的直径, Δγ=1-/m,,是气体常数,是液体粘度, 可以用Fulcher方程表示为:
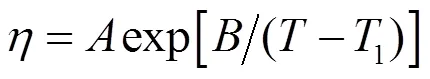
其中,和1是依赖于具体材料的常数.
方程(1)左边第一项描述固体中的热变化, 右边第一、第二和第三项分别描述熔体流向固体的热、固体流向冷模的热以及液体流向固体的热. 方程(1)与文献[16]中方程(3)相似, 所不同的是, 由于模型中正温度梯度的存在, 在方程(1)中加上了右边第一项.
对于Pd82Si18, 前面提到的参数取为:s= 10.2×103kg/m3,= 71.18 Wm-1K-1,0=300 K, Δm= 116.7×103J/kg,0= 2.0×10-10m,m= 1 071 K,= 6.32×10-5Ns/m2,= 3 730 K,1= 557 K.
在很短时间之后固体中达到定态时, 对于给定0, 温度对时间的导数为0. 假定液体中温度分布为线性时方程(1)变为:

其中是快冷熔体厚度, 上标S表示定态. 当为100 μm或者更小时, 热传输可以表征为Newtonian冷却方式[16], 基于这个考虑, 本文中选为5.0×10-4m.
对方程(2)和(4)进行数值求解, 结果示于图2. 需要指出的是, 为了计算简单, 本文中取0 m.
2 结果与讨论
Wang[4]等人指出, 薄片急冷凝固的准确计算需要知道确切的薄片与衬底间热传输指数大小, 但是热传输指数难以测量. 现在人们通常认为, 对于典型急冷条件, 热传输指数可能在1.0×105~5.0×105W·m-2K-1范围内[4]. 从图2可以看出, 当冷模温度0慢慢从900 K降低到300 K时, 对于2.0×105~5.0×105Wm-2K-1范围内的热传输指数, 多定态现象会发生. 这意味着在典型急冷条件下, 当冷模温度0缓慢降低时, 多定态会发生.
对于一个反应-扩散方程:


从图2可以看到, 当过冷金属液体急冷, 冷模温度以足够慢的速度降低使固体温度达到定值时,对于热传输指数= 2.0×105W·m-2K-1, 定态温度首先沿着曲线连续降低到, 在这个临界温度点, 由于对应于曲线的定态的非稳定性, 突然降低到, 最后沿曲线连续降低.
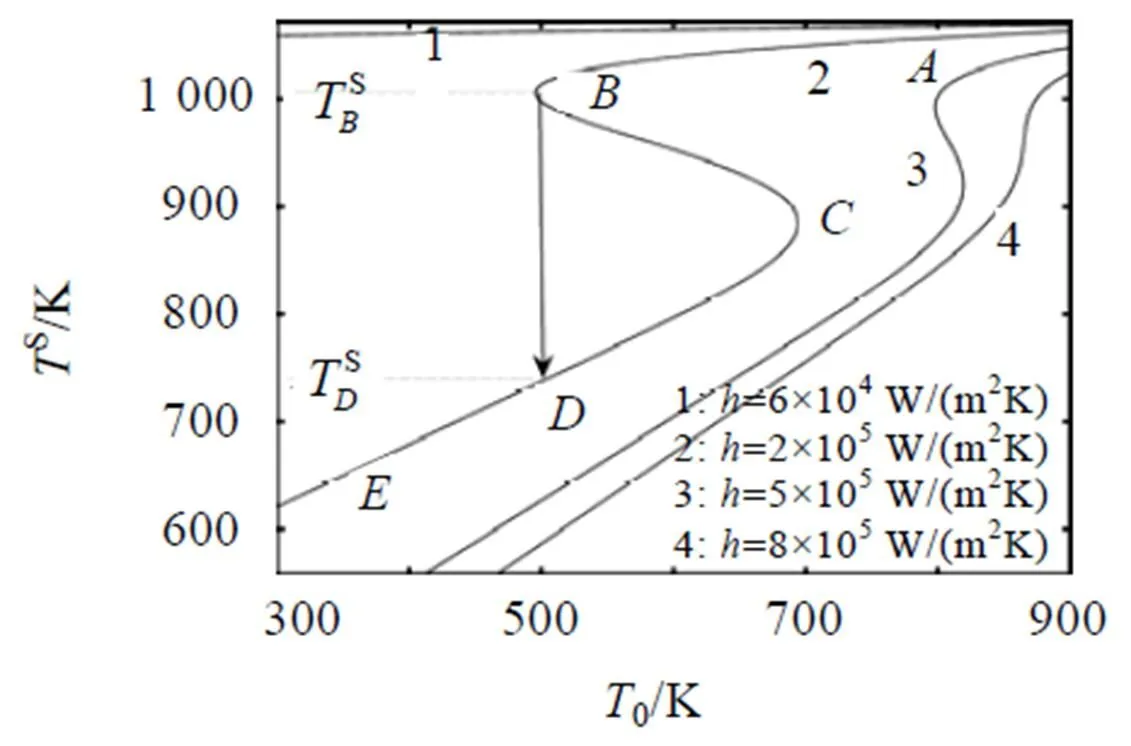
图2 某些热传输指数值下, 随冷模温度从900 K降低到300 K时固体中定态温度的变化情况
在这个模型中, 定态方程(3)是非线性的, 当冷模温度0处于一定范围时, 方程(3)有多个根. 在这些根里面, 一个是不稳定的, 而其它两个是稳定的. 定态方程的非线性使得定态温度产生了突然的下降.
应该指出, 前面只考虑固体和液固界面的定态温度变化. 不过, 对于靠近液固界面随界面移动着的薄层液体来说, 可以认为其温度与液固界面上的相同并且以相同趋势变化.

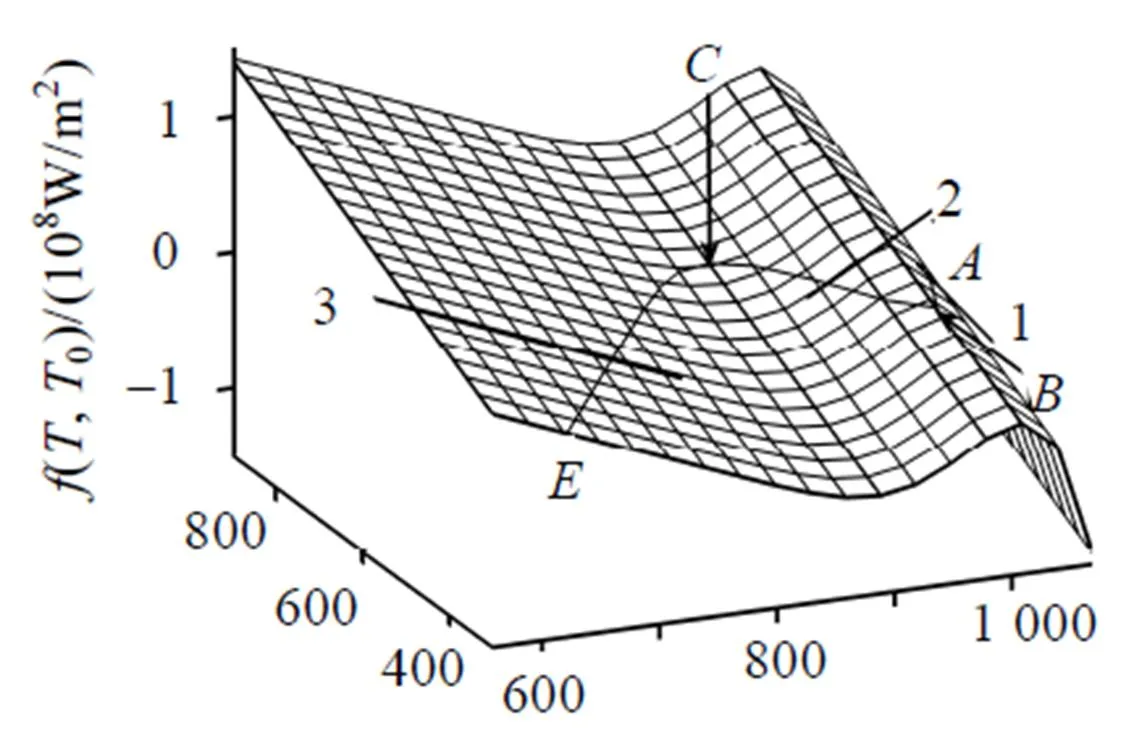
图3 函数f随固体中温度和冷模中温度变化而变化的情况
计算表明, 当Biot数/小于0.015[2]时, 热传输为Newtonian冷却方式. 在模型中, Biot数为1.4, 这意味着冷模和薄片间的热传输应该为中间冷却方式. 这也证实了前面的假定, 即液体存在大的温度梯度是合理的.
3 结论
用分支理论研究了合金Pd82Si18的单向凝固模型, 试着从动力学方面对急冷过程得到更进一步的了解. 计算表明, 在Pd82Si18的急冷过程中, 当冷模温度足够慢地从900 K下降到300 K时, 对应2.0×105~5.0×105W/m2K范围内的热传输指数, 多定态现象发生. 伴随着定态间的跃变, 玻璃转变很可能发生.
[1] Fukai J, Ando T. Microstructure development in alloy splats during rapid solidification[J]. Mater. Sci. Eng. A, 2004, 383(1): 175-183.
[2] Yeh F B, Wei P S, Chiu S H. Distinct property effects on rapid solidification of a thin liquid layer on a substrate subjectto self-consistent melting[J].J. Crys. Growth, 2003, 247(3-4):563-575.
[3] Wang G X, Prasad V. Microscale heat and mass transfer and non-equilibrium phase change in rapid solidification[J]. Mater.Sci. Eng. A, 2000, 292(2): 142-148.
[4] Wang G X, Matthys E F. Modeling of heat transfer and solidification during splat cooling: effect of splat thickness and splat/substrate thermal contact[J].Int. J. Rapid. Solidification, 1991, 6(2): 141-174.
[5] Clyne T W. Numerical treatment of rapid solidification[J].Metall. Trans. B, 1984, 15: 369-381.
[6] Levi C G, Mehrabian R.Heat flow during rapid solidification of undercooled metal droplets[J]. Metall. Trans. A, 1982, 13: 221-234.
[7] Clyne T W, Garcia A.The application of a new solidification heat flow model to splat cooling[J]. J. Mater. Sci., 1981, 16(6): 1643-1653.
[8] Miyazawa K, Szekely J. A mathematical model of the splat cooling process using the piston and anvil technique[J]. Metall. Trans. B, 1979, 10(3): 349-358.
[9] Shingu P H, Ozaki R. Solidification rate in conduction cooling[J].Metall. Trans. A, 1975, 6(1): 33-37.
[10] Ruhl R C. Cooling rates in splat cooling[J]. Mater. Sci. Eng., 1967, 6(1): 313-320.
[11] Nitzan A, Ross J. Oscillations, multiple steady states, and instabilities in illiminated systems[J]. J. Chem. Phys., 1973, 59(1): 241.
[12] MAY R M. Stability and Complexity in Model Ecosystems[M]. Princeton: Princeton University Press, 1973: 84.
[13] Crell C L, Ross J. Multiple stationary states and hysteresis in a chemical reaction[J]. J. Chem. Phys., 1976, 65(9): 3779.
[14] Cao B, Chen Z H. Multiple steady states in rapid solidification and the glass transition[J]. Science in China. E, 1998, 41(3): 247-254.
[15] Cao B, Chen Z H. Bifurcation theory model for the glass transition[J]. Physica B, 1999, 266: 152-161.
[16] Fredriksson H, Östlund A, Söderhjelm H et al. Rapidly Quenched metals[A]. Proc. 5th. Int. Conf. on Rapidly Quenched Metals[C].Amsterdam,The Netherlands: North-Holland, 1985, 1: 187.
[17] Davies H A, Lewis B G. Metallic glasses and the avoidance of crystallization in metallic melts[J]. Fara. Disc. Chem. Soc., 1976, 61: 100-109.
[18] Sattinger D H. Topics in Stability and Bifurcation Theory[M]. Berlin: Springer, 1973: 77.
[19] Minorsky N. Nonliear Oscillations[M]. Princeton, Newjersey: Van Nostrand Company, 1962: 213.
[20] Dyre J C. The glass transition and elastic models of glass-forming liquids[J]. Rev. Mod. Phys., 2006, 78(3): 953-972.
[21] Chen H S, Turnbull D. Formation, stability and structure of palladiumesilicon based alloy glasses[J].Acta. Met., 1969, 17: 1021-1031.
Multiple steady states during splat cooling studied by the bifurcation theory
ZHANG Ai-long
(College of Physics and Electronics, Hunan University of Arts and Science, Changde 415000, China)
A splat cooling process of alloy Pd82Si18is modelled to analyze the effect of the heat transfer coefficient, which is difficult to determine experimentally, on solidification variables. It is shown that, multiple-steady-states phenomenon occurs for the heat transfer coefficient ranging from 2.0×105W/(m2K) to 5.0×105W/(m2K), when the temperature in the cold mould0decreases sufficiently slowly from 900 K to 300 K. There is an abrupt temperature drop, with which the glass transition might take place, at the liquid-solid interface, when0approaches a marginal value.
splat cooling; multiple steady states; glass transition
TG 111.3
1672-6146(2012)01-0032-04
10.3969/j.issn.1672-6146.2012.01.009
2012-03-09
湖南文理学院博士科研启动项目(13101009)
张爱龙(1975-), 男,博士, 研究方向为金属玻璃理论及模拟.E-mail: islandwithfire@hotmail.com
(责任编校:刘刚毅)
