基于CF滤波的国际干散货航运市场周期性分析

林国龙，陈言诚

(上海海事大学 科学研究院，上海 201306)

0 引言

国际干散货航运市场是国际航运市场的重要组成部分，影响其波动的因素较多，其中主导影响因素是干散货航运市场的供给与需求关系.供给反映的是干散货航运市场自身规模的发展，需求反映的是国际干散货贸易的发展，而波罗的海干散货运价指数(Baltic Dry Index，BDI)是对供需变动的反映.［1］观察BDI的历史数据，不难发现市场呈现周期性波动，且周期时间长度正在逐渐缩短，分析国际干散货航运市场的周期性特征有助于对该市场形成整体性的理解，也有助于进行宏观决策.

根据STOPFORD［2］的理论，将航运市场的变化具体分为3种不同性质的周期:长周期、短周期和季节性周期，分别呈现波谷、复苏、波峰和衰退等4个阶段，与经济周期有很大的相关性.干散货航运市场的周期性波动主要是由市场供给与需求关系的失衡造成的，当供给大于需求时，市场处于衰退阶段直至波谷;反之，市场处于复苏阶段直至波峰.杜昭玺等［3］选用1999年11月到2008年4月的BDI月度数据作为研究对象，分别对BDI的季节性和周期性波动规律进行研究，得出BDI长期波动趋势，近8 a来BDI的周期在3.0～3.5 a.王磊等［4］运用谱分析方法研究海岬型船平均营运收入与新船价格之间的周期波动关系，得出两者的波动周期为3～5 a，并且新船价格的变化比营运收入变化滞后约4个月.刘子建［5］选用1985—2009年的BDI季度数据作为研究对象，运用小波理论研究干散货市场周期波动，得出BDI长周期是16 a，短周期是4 a.

综上所述，近年来学者对干散货航运市场的周期性研究对象大多只选择BDI指数，主要运用去除趋势和季节、谱分析和小波分析等方法，而没有将两种以上的方法结合起来对干散货航运市场的若干子市场进行整体性研究.本文通过运用CF(Circle－Frequency)滤波与谱分析相结合的方法，研究干散货航运市场的新造船市场、二手船市场、拆解船市场、运费市场和干散货贸易市场的周期性及其相互关系，以达到对干散货航运市场周期的整体性分析.

1 研究框架

研究对象包括干散货航运市场新造船价格(PN)、二手船价格(PS)、拆解船价格(PD)、BDI和干散货贸易量NT.具体研究框架见图1.

2 方法介绍

2.1 Census X12季节调整

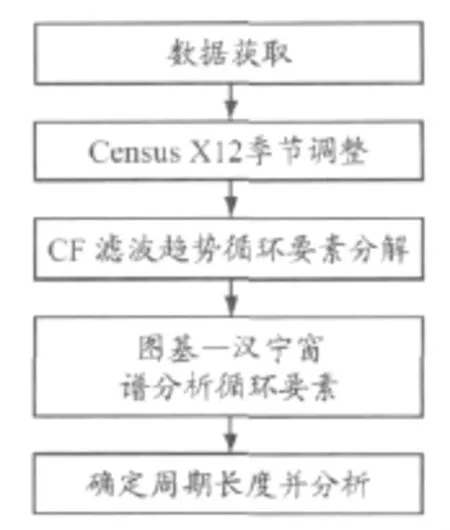
图1 研究框架

Census X12［6］季节调整程序是美国商务部人口普查局在X11方法的基础上发展而来的，将时间序列(Yt)分解成趋势循环要素序列(TCt)、季节要素序列(St)和不规则要素序列(It)，以确保能够反映时间序列运动客观规律的趋势循环要素被分离出来.主要调整模型有4种形式:乘法、加法、伪加法和对数加法模型.本文主要应用乘法模型，其特点是可以避免计量单位的影响，增强不同经济变量之间的可比性，其一般形式为Yt=TCtStIt，具体计算有3个步骤.

(1)季节调整的初始估计，又分为5小步.

①通过中心化12项移动平均计算趋势循环要素的初始估计

②计算季节和不规则要素SI项的初始值

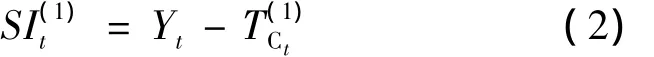
③通过3×3移动平均公式计算季节因子S的初始估计

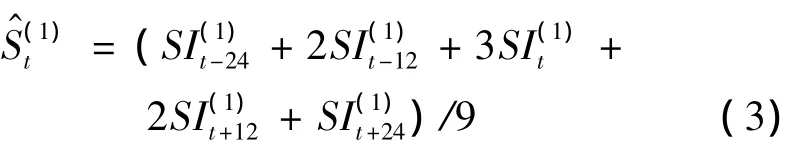
④消除季节因子中的残余趋势

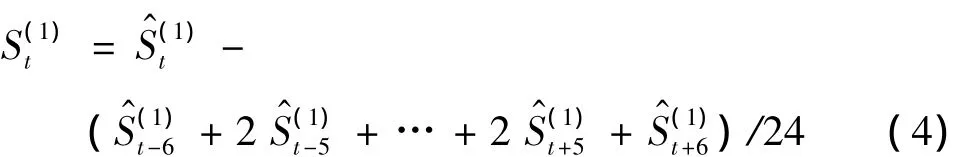
⑤季节调整结果的趋势循环和不规则要素初始估计

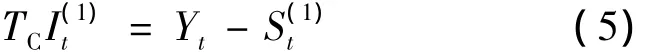
(2)计算暂定的趋势循环要素和最终的季节因子，又分为5小步.

①利用Henderson移动平均公式计算暂定的趋势循环要素

②计算暂定的季节和不规则要素SI项

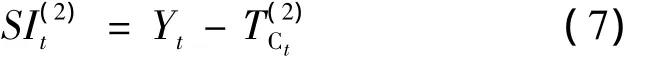
③通过3×5项移动平均计算暂定的季节因子

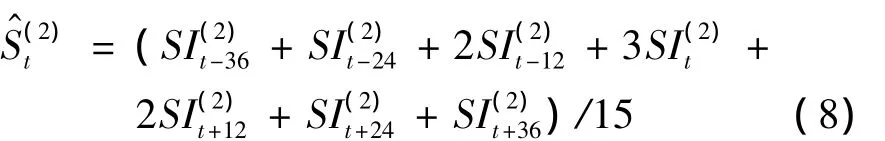
④计算最终的季节因子

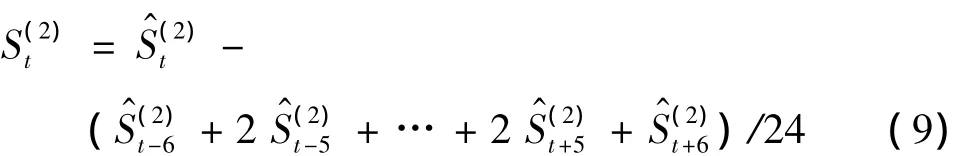
⑤季节调整的第2次估计结果的趋势循环和不规则要素

(3)计算最终的趋势循环要素和最终的不规则要素，又分为2小步.

①利用Henderson移动平均公式计算最终的趋势循环要素

②计算最终的不规则要素

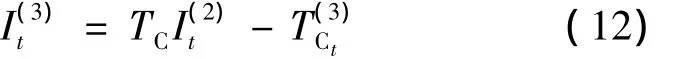
2.2 CF滤波趋势分解

趋势循环要素分解的方法有很多，在研究周期性中广泛使用的滤波技术主要有3种:HP滤波、BK滤波和CF滤波.其中，HP滤波为高通滤波，BK滤波和CF滤波为带通滤波.本文采用CF滤波方法.

CF滤波是一种全样本非对称带通滤波，此方法是众多滤波方法中较新的一种，是 CHRISTIANO等［8］对BK滤波进行改进后提出的，与HP滤波(只过滤掉低频的周期成分而把剩余部分作为周期成分)和BK滤波(过滤掉低频的趋势成分和高频的不规则波动成分，并且会损失样本数据)不同，CF滤波具有充分的灵活性，不但对不同性质的时间序列采用不同的滤波公式，而且在同一时间序列不同时间点的估计也选取不同的阶段和权重［7］，不损失样本数据，能够过滤掉总量在全样本期的趋势.同时，可以根据研究数据的需要分离出特定周期长度的循环要素，并考虑数据的时序特征和平稳性特征，分解出的周期性成分更为客观、准确.其所采用的计量模型［8］如下:

假设yt是从一个总量时间序列xt在2π/w－m到2π/w－

n频带之间分离出来的周期，即

式中:L是滞后算子;B(L)是理想的带通滤波，可以写成

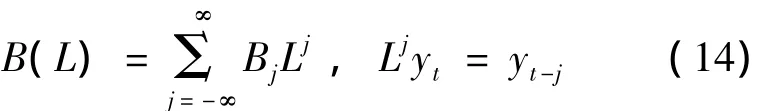
然而，理想带通滤波只适用于无穷数列，因此CHRISTIANO 等［8］提出通过近似估计yt=B(L)xt，并依据残差值平方和期望最小化原则使得在最大程度上近似y，即t

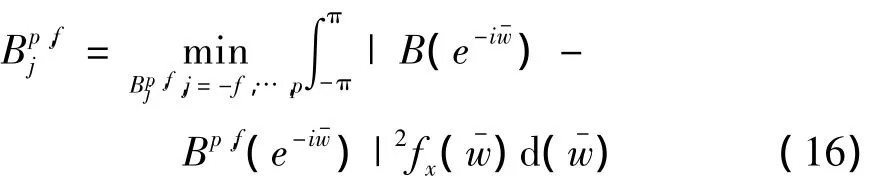
式中:fx()是总时间序列 xt在频带的谱，CHRISTIANO等［8］采用假设数据产生服从随机游走过程的方法求解.

2.3 谱分析

时间序列{Xt|t=0，1，2，…，n}的谱密度或标准谱密度函数是周期波动谱分析的重要内容.一般对谱密度函数进行加窗处理得谱密度的窗谱估计，常见的窗函数有矩形窗、巴特利特窗、图基—汉宁窗、帕曾窗等.在选择窗函数时，窗谱主瓣尽可能窄以获得较陡的过渡带，尽量减少窗谱最大旁瓣的相对幅度以减小肩峰和波纹.在以上几种窗函数中，图基—汉宁窗的旁瓣相对较小，不易产生谱泄露，对输出信号的频率分析精度影响较小，所以本文采用图基—汉宁窗谱估计法［9－10］.其计算步骤如下:

(1)计算时间序列{Xt}的样本自协方差函数R^(k)和样本自相关函数r^(k)

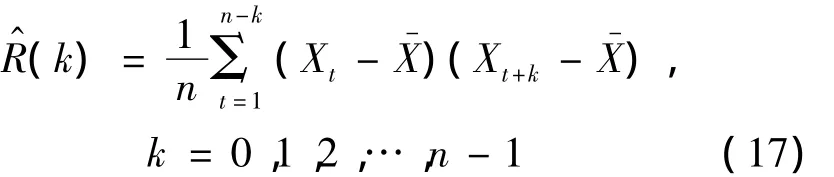
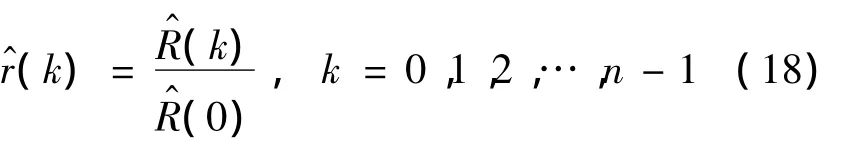
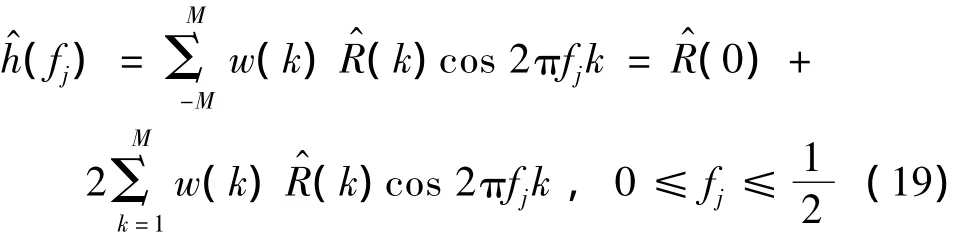
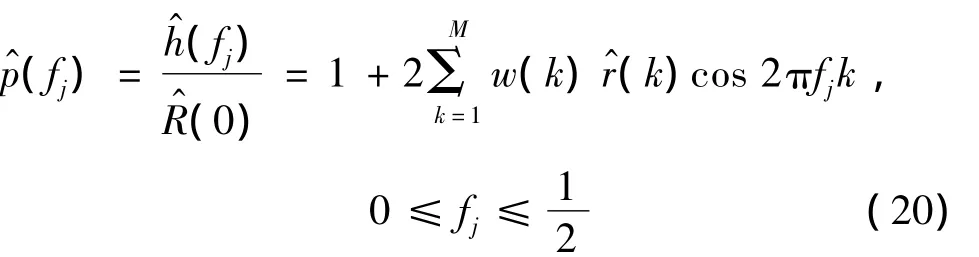
为图基—汉宁滞后窗.

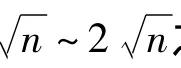
3 实证研究

运用以上理论方法，使用EViews和MATLAB求解，选取干散货航运市场 IBD，PN，PS，PD和 NT等5大市场的月度数据，IBD，PN和PS数据从1985年1月到2011年6月，NT数据从1991年1月到2010年12月，PD数据从1995年11月到2011年6月.(数据来源于Clarkson网站)

3.1 Census X12季节调整

首先对数据取对数处理，分别记为LBDI，LNP，LSP，LDP和LTN.然后用Census X12季节调整法去掉季节和不规则要素，得到只包含趋势循环要素的序列LBDI_TC，LNP_TC，LSP_TC，LDP_TC和 LTN_TC，见图2.

图2 循环趋势要素序列

3.2 CF滤波分析

用CF滤波分析所得到的趋势循环要素序列，考虑到数据的时间长度，将分离长度定为18～84个月的周期成分.将该序列进行趋势循环分解，得到图3所示的趋势(Trend)循环(Cycle)分解图.

从图3可以得到5大市场循环周期波动图(见图4).从图4可知，5大市场的循环周期波动序列的循环周期波动时间呈逐渐缩短且波动幅度呈增大趋势，唯有NT的波动幅度较为平稳，因为干散货主要由铁矿石、煤等不可再生资源组成，其波动幅度有限.观察循环周期波动图，在NT增长的带动下，将会引起IBD的上涨，两者的反应几乎同时进行，呈现同升同跌的趋势，而随后PN，PS和PD也随之上涨.

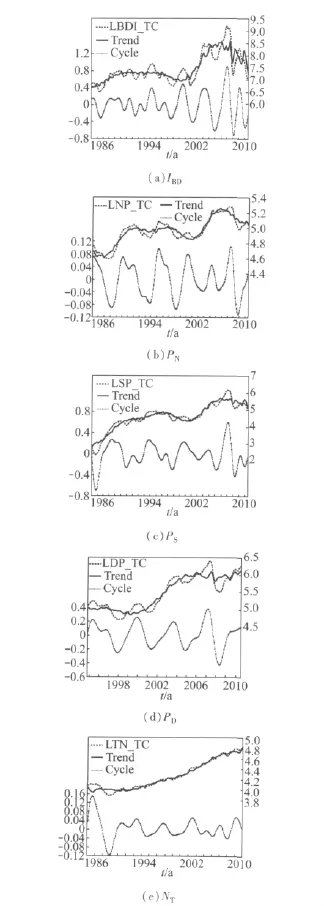
图3 趋势循环分解图

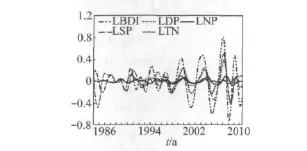
图4 5大市场循环周期波动

为此，运用 Granger因果关系检验［6］分析5大市场循环周期波动之间的相互影响关系.从表1可知，在5%的临界值下，NT与IBD存在单向的影响关系，表示IBD不会影响NT，但NT会影响IBD的变化，而IBD与PN，PS和PD之间呈现相互影响的关系.因为IBD的上涨，引起船舶所有人看好未来市场，船舶所有人会因为较高的运费想要获取更多的收益，作出增加新船订购量和二手船购买量的决策，引起PN和PS也随之上涨，拆解船市场由于干散货市场前景明朗，船舶所有人都不愿意将船舶进行拆解，导致拆解船市场呈现量跌价涨的现象，反之亦然.

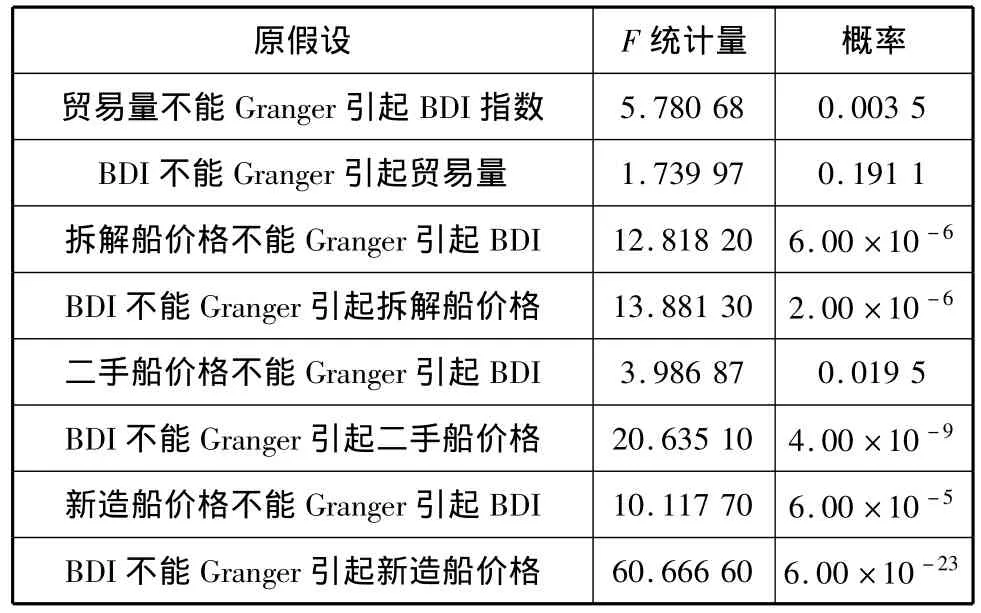
表1 Granger因果关系检验结果

同时，观察循环周期波动图的波谷和波峰时发现，BDI循环周期波动的波谷和波峰都领先新造船市场、二手船市场和拆解船市场大约5～12个月，充分说明BDI作为国际干散货航运市场上的“晴雨表”，成为其他相关市场的领先指标.随着航运市场技术的飞跃发展和市场反应速度的加快，BDI的领先时间正在逐渐缩短.

从图3的循环周期波动图的波动轨迹还能粗略得到循环要素序列的周期情况，为了得到循环要素序列精准的周期，采用谱分析方法计算出各循环要素序列波动的周期.

3.3 谱分析

在进行谱分析时，首先需要对循环要素序列进行平稳性检验，本文采用PP检验［6］，检验出循环要素序列均为平稳序列.随即对循环要素序列进行图基—汉宁窗谱分析，窗函数M分别取60和80，得到图5所示的周期图谱.

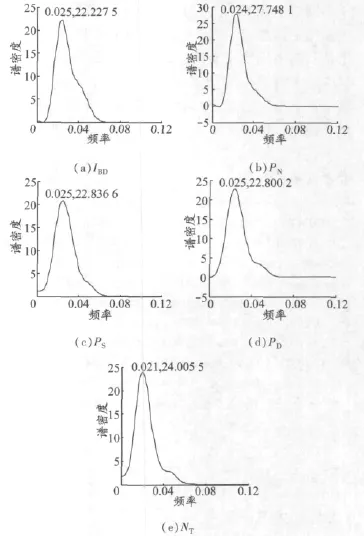
图5 各循环要素周期图谱

从图5可知:PN的频率为0.024，周期约为42个月;PS，PD和IBD的频率都为0.025，周期约为40个月;NT的频率为0.021，周期约为48个月.由此可推出，市场的波动周期在3.5 a左右，这与全球航运市场分析家SHIRISH Nadkarni在其研究航运业周期论文中指出的全球性航运周期已经从原来的7 a左右缩短到最近的3～4 a的结论一致，这正是干散货航运市场供给与需求关系不断变化的结果.在供给与需求平衡状态，世界经济的发展带来干散货贸易量的变化，破坏供给与需求关系的平衡;当需求大于供给时，运费上升，带来新造船和二手船市场的繁荣，市场进入高峰期;随着新造船数量不断增多，拆解船数量减少，导致市场供给大于需求，迫使运费下降，市场进入低谷期，此时拆解船市场变得活跃，致使供给与需求达到新的平衡，如此循环往复地进行着国际干散货航运市场的周期性变化.这为从事干散货航运的经营者进行经营决策提供重要的依据，使其可在市场波动周期的基础上，根据市场的发展趋势和淡旺季状况进行合理决策.

4 结束语

通过运用CF滤波分析国际干散货航运市场中的新造船市场、二手船市场、拆解船市场、BDI和干散货贸易市场的周期性波动，发现干散货航运市场具有以BDI或干散货贸易量为领先指标，继而影响其他3个市场的发展趋势;运用谱分析方法计算干散货航运市场的周期长度，发现市场的波动周期约为3.5 a.目前，干散货航运市场的供给远远大于需求，反映出BDI正处于低谷时期，根据3.5 a的航运市场周期推算，预计要到2013后才能出现航运市场高峰期.干散货航运市场经营者可以根据这个市场周期，结合实际的世界经济形势、干散货贸易需求、新造船、二手船、拆解船市场和其他相关市场状况进行有效的市场预测，合理调节运力结构，以规避风险、提高效益.

［1］ROBERT A.The bulk shipping business:market cycles and shipowners’biases［J］.Maritime Policy ＆ Manage，2007，34(6):577－590.

［2］STOPFORD M.Maritime economics［M］.London:Taylor＆ Francis，2008:93－133.

［3］杜昭玺，李阳，靳志宏.波罗的海干散货运价指数预测及实证分析［J］.大连海事大学学报:社会科学版，2009，8(1):77－80.

［4］王磊，李序颖.海岬型船平均收益与新造船价格波动相关性的互谱分析［J］.上海海事大学学报，2010，31(3):74－77.

［5］刘子建.基于小波理论的国际干散货航运市场周期波动及预测研究［D］.大连:大连海事大学，2009.

［6］高铁梅.计量经济分析与建模:EViews应用及实例［M］.北京:清华大学出版社，2009.

［7］汤铎铎.三种频率选择滤波及其在中国的应用［J］.数量经济技术经济研究，2007(9):144－156.

［8］CHRISTIANO L J，FITZGERALD T J.The band pass filter［J］.Int Econ Rev，2003(44):435－465.

［9］马叶江，胡思继，武旭.运输经济周期波动的谱分析测定方法［J］.北京交通大学学报，2008，7(2):12－15.

［10］王磊，李序颖.基于谱分析的波罗的海干散货运价指数周期研究［J］.数理统计与管理，2011，30(6):1051－1059.