用于视频多播传输的压缩传感实现方法研究*

赵慧民，郭一缜,丁晓艳，朱 立

(1.广东技术师范学院电子与信息学院，广东 广州 510665；2.西安邮电学院通信与信息工程学院，陕西 西安 710121)

在不同信道条件下,研究实现视频数据同时可靠地传输到多用户终端，且满足固定码率和低失真的要求，是目前多播通信系统研究的焦点技术。按照Shannon’s的传统理论，在给定信道容量时，信源和信道编码分部进行实现。但是，在多用户环境下,这种技术很难达到信源和信道的优化编解码。例如，MPEG视频采用可变长编码(VLC)设计，即使出现单个编码错误，也能传播很长时间并导致码率较大失真。因此,传统的多播通信系统存在资源优化分配问题。

根据多播通信的可变信道统计及其系统响应的条件，文献[1]提出一种联合信源信道编码(JSCC)的实现方法。其目的是，把一部分视频失真通过信道编码处理而不是在信源编码时考虑。实际上，JSCC是通过多分辨率编码结合非均匀错误保护 (UEP)实现[1-2]。但这种实现技术增加了系统实现的复杂性。

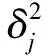
针对视频多播的实际情况，本文基于最新的压缩传感理论，结合信源信道编码技术，提出并实现了一种稀疏表示的视频数据解码方法，旨在降低传输视频数据失真并提高恢复图像的质量[4-5]。

1 压缩传感理论

1.1 图像信号的测量

对于给定的一组稀疏基Ψ∈RN×N，如果图像信号x能表示成Ψ中K个(K≪N)非零系数的线性组合，则称x为K稀疏信号，其表示形式为

ψisi=Ψs

(1)

这里，s∈RN表示K稀疏矢量系数。这说明，信号x在稀疏基Ψ上可通过s的N个系数中K个非零项表示。因此，把x用测量矩阵Φ投影到一个M(M≪N)维的空间上，可得到一个线性测量值y∈RM:

y=Φx=ΦΨs∈RM

(2)

压缩传感理论说明，只要矩阵Φ和Ψ满足约束等距性条件，且s足够稀疏，则通过测量值y可以高概率恢复原图像信号x。

1.2 图像信号的恢复

信号的恢复是指由M次(M≥cKln(N/K))测量向量y重构长度为N(M≪N)的稀疏信号x的过程。Candes 等证明了信号重构问题可以通过求解最小l0范数问题加以解决[5-6],即

(3)

(4)

问题(P1)可以转换为如下最小l1范数问题:

(5)

Candes等说明了，当测量矩阵为I.I.D随机高斯矩阵N(0,δ2)时，有条件：

(6)

公式(5)和(6)构成了本文恢复视频图像的基础。

2 提出的实现方案

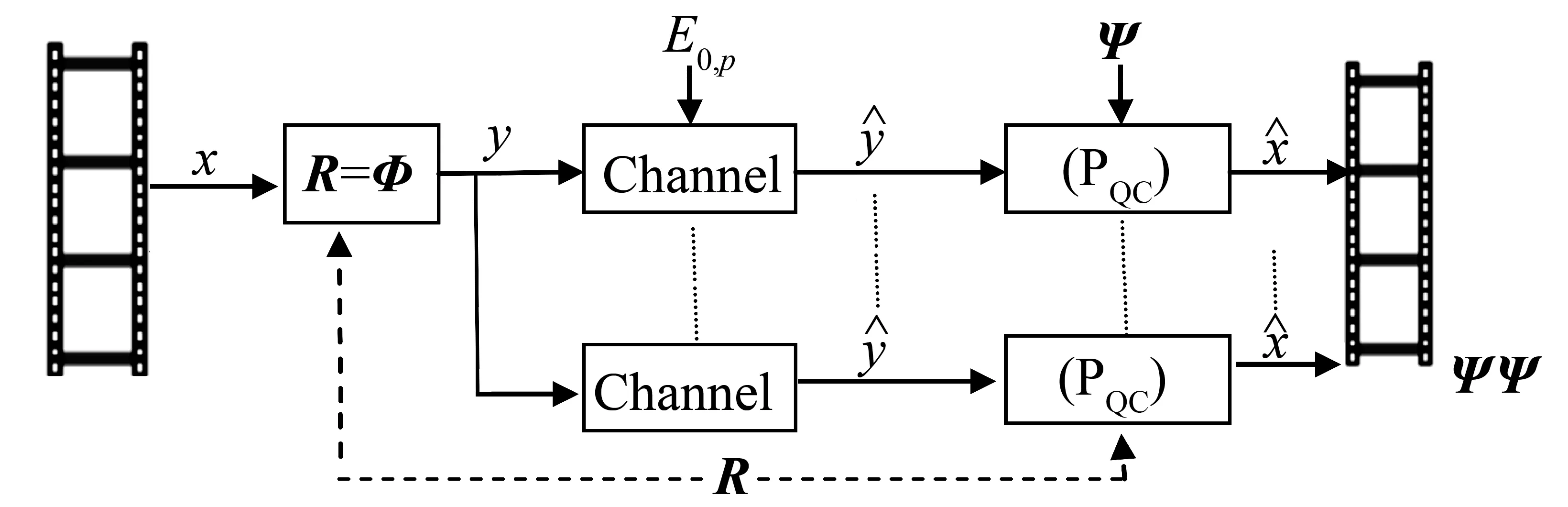
图1 多播通信系统研究的目标对象 Fig.1 Research object of the multicast communication system

2.1 信道模型

假设灰度图像被分解为n×n块，一个块的数据通过矢量长度为N=n2列矩阵表示。对每一块数据通过稀疏基Ψ变换得到x，用视频帧的每一个块数据x减去帧均值，然后通过满秩随机矩阵R=Φ∈RN×N对x进行测量得到测量值y。这些测量数据y通过块交织并成为传输的数据包。其中，随机矩阵R可以用高斯随机矩阵G、正交高斯随机矩阵G⊥、贝努利B以及哈达玛矩阵H实现。而通常的稀疏基可以根据信号本身的特点灵活选取,常用的有离散余弦变换DCT基、快速傅里叶变换FFT基、离散小波变换DWT基、Curvelet基、Gabor基以及冗余字典等。

为了分析传输性能，这里假设两种可能的信道模型。在两种情况下，我们都可以直接使用模拟值进行测量转换和基带传输。

第一种信道模型是包丢失率为p的加性高斯白噪声(AWGN)信道，其噪声值加到测量值y使信道信号噪声比(CSNR)满足条件[8]：

/

(7)

第二种信道模型是无噪声理想网络信道。这种情况就是有界无穷CSNR噪声信道。其研究的目的是，为了折中有噪信道和有损信道之间的性能参数之间的关系。

2.2 数据解码处理

压缩传感测量数据y被解码之前，按照传输包丢失模型，需要对每个块构造随机矩阵。然后，估计噪声级参数。如果编码器使用随机矩阵R∈RN×nN来生成测量数据y，那么，一个给定块中的N个测量数据之中，可通过S∈{1,2,…,N}进行索引，其基数性为|S|=M。则，我们在接收端构造的随机矩阵形式为：

ΦT={(RT)i|i∈S}

(8)

因此，在稀疏基下，根据视频帧内图像系数的分布特性及其视频帧间相关性，我们研究通过如下方法提高视频图像恢复的性能。

2.2.1 视频帧内的重加权解码 在变换域，利用图像系数的分布特性，可以改善图像的恢复质量。我们定义一个对角加权矩阵Λ如下：

(9)

式中，参数0<γ≪1是si的调节因子，因此，重加权l1范数实际上近似等于l0范数，即有关系式：

‖Λs‖1=∑i|Λiisi|=

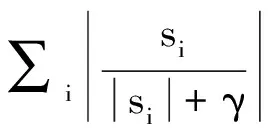
(10)

则，重加权l1范数最小化形式为：

(11)

代入参数q=Λs,上式可以写为：

.t.ΦΨΛ-1q‖2<ε

(12)

即有

(13)

但自然图像系数并非I.I.D均匀分布，因此，在一帧内，我们使用每个系数的方差作为幅度估计，并按照下式关系在重加权最小化计算中引入此参数：

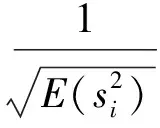
(14)

2.2.2 视频帧间解码 由于一个连续视频帧的相关性取决于运动矢量的特性，因此，借助于Prades-Nebot和Marcia等研究的分布视频编码DVC(Distributed Video Coding)的原理结果[9]，在不增加解码器复杂性的情况下，我们提出一种基于帧间相关性的运动矢量解码方法，以实现多帧接收数据的解码及其连续图像的重构。

首先考虑两个连续帧之间的解码。设前一帧(即帧1)作为下一帧(帧2)的参考，在此两帧之间估计局部运动矢量。对于帧2所要恢复图像的j块，我们取帧1对应的j块周围可能的取值路径作为扫描矢量进行稀疏表示，其形成的矩阵设为Ψ(j)，但它不是一个完备基。因此，需要通过运动矢量使两个帧高度相关，才会形成一个完备基。这时，最佳原子的索引，就是围绕块j在两个帧之间对运动矢量v的估计。

运动矢量v估计之后，两帧稀疏基的公共部分组成一个联合基，并最终生成一个超完备字典使s高度稀疏。最终，我们得到的稀疏基形式如下：

(15)

这里，变换Tv(Ψ)(·)表示运动矢量v(j)生成的某种转移矩阵。如果sjoint表示了两个连续图像数据块的稀疏系数，那么，连续两个帧的稀疏值系数(s1,s2)表示如下：

Ψs=Ψ

(16)

其中，每个数据块的大小决定了运动估计的搜索空间，而使用循环转移变换T(·)可优化稀疏基的联合设置。同样的方法可以应用于3个或更多连续帧的稀疏值表示。

3 实验结果

为了更好地估计噪声信道和有损信道对CS解码的影响，在定义信道各种丢失率p和CSNR的情况下,我们用MATLAB对视频football序列进行实验，并用峰值信噪比PSNR作为比较的度量单位。PSNR定义如下：

(17)

1)测量矩阵和稀疏基的选取:为了更好地确定实验参数之间的折中关系，结合不同的测量矩阵R和稀疏基Ψ，实验在各种参数下的结果如图2所示。图2中，R=G表示高斯随机矩阵，R=G⊥为高斯正交随机矩阵，R=HD代表哈达玛矩阵。Ψ=DT为DCT基，Ψ=WT表示离散小波基。由图可见，当G⊥和D结合并对图像压缩数据解码时，图像具有最好的恢复功能，而其它情况稍差，但这种差别很小。

2)重加权解码：在不同的CSNR噪声环境下，图3说明了经过重加权l1范数处理后图像的恢复结果。可见，当包丢失率p较大时，重加权l1范数解码恢复的图像比仅采用l1范数对图像恢复的PSNR提高了1-2 dB增益[10]。

图2 应用不同测量矩阵Φ和稀疏基Ψ恢复图像的性能比较

图3 分别采用l1范数和重加权解码恢复图像的性能比较

3)帧间编码:使用8×8块进行运动估计和图像重构。图4在不同的CSNR噪声环境下，说明了基于运动矢量解码与稀疏解码恢复图像的性能比较曲线。总体而言，在较低CSNR时，基于运动矢量解码形成的过完备基比稀疏解码生成的完备基改善了1 dB的增益。

4)与软投影解码比较：在各种相同条件下，使用与R=G⊥与Φ=D(即本文最好的配置方案)结合重加权l1范数解码和软投影方法进行性能比较，结果如图5所示。图中在较低信道噪声和较高的包丢失率情况下，本文实现的重加权l1范数解码方法具有较好的性能。而在较高信道噪声和较低的包丢失率时，本文方法和软投影技术性能相当。

4 结论与讨论

基于压缩传感理论，在较高的传输包丢失率和一定的信道噪声环境下，本文提出了一种应用于视频多播技术的重加权l1范数解码和基于运动矢量的帧间编码，并在此技术应用条件下，研究了各种测量矩阵和稀疏基表示。本文的优点是，编码器简单可靠且能根据用户的数量调整资源分配问题；而在解码端，可自由选择稀疏基表示和视频帧的相关性模型。其缺点是，增加了接收端的复杂性，需要解决优化解码问题。未来的工作，根据压缩传感技术特性，在传输少量边信息情况下，进一步研究视频序列的相关性以实现更高的图像质量和图像传输的安全性问题[11-12]。

图4 基于运动矢量解码与稀疏解码恢复连续图像的性能比较

图5 本文和软投影方法恢复图像的性能比较

参考文献：

[1]HE Z,CAI J,CHEN C.Joint source channel rate-distortion analysis for adaptive mode selection and rate control in wireless video coding[J].IEEE Transactions on Circuits and Systems for Video Technology,2002 (12):511-523.

[2]赵慧民，方艳梅.一种非均匀错误保护实现最优码率分配的技术[J].中山大学学报：自然科学版，2007，46(1)：43-47.

[3]JAKUBCZAK S,RAHUL H,KATABI D.One-size-fits-all wireless video[G].HotNets,2009.

[4]杨海蓉,张成,丁大为,等.压缩传感理论与重构算法[J].电子学报，2011(1):142-148.

[5]CANDES E,WAKIN M,BOYD S.Enhancing sparsity by reweighted l1 minimization[J].Journal of Fourier Analysis and Applications,2008(14): 877-905.

[6]DONOHO D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4): 1289-1306.

[7]李树涛,魏丹.压缩传感综述[J].自动化学报,2009,35(11):1369-1377.

[8]赵慧民，朱立，张光昭.率失真最优自适应量化及其系数阈值的设定[J].中山大学学报：自然科学版，2004，43(3)：32-35.

[9]PRADES-NEBOT J,MA Y,HUANG T.Distributed video coding using compressive sampling[R].Proceedings of the Picture Coding Symposium ,2009.

[10]MARCIA R,WILLETT R.Compressive coded aperture video reconstruction[C]∥Proc European Signal Processing Conf(EUSIPCO 1),2008.

[11]SEBERT F,ZOU Y M,YING L.Toeplitz block matrices in compressed sensing and their applications in imaging[C]∥Proceedings of International Conference on Technology and Applications in Biomedicine.Washington D C,USA: IEEE,2008: 47-50.

[12]GOYAL V,FLETCHER A,RANGAN S.Compressive sampling and lossy compression[J].IEEE Signal Processing Magazine,2008,25(3): 48-56.