带交叉扩散项的捕食模型非常数正解的存在性*
2012-05-09王利娟姜洪领
王利娟,姜洪领
(1.陕西师范大学数学与信息科学学院,陕西 西安 710062;2.宝鸡文理学院数学系,陕西 宝鸡 721013 )
本文考虑如下带交叉扩散项的捕食食饵模型:
(1)
其中u,v分别代表食饵和捕食者的密度,Ω是Rn(n≥1)中具有光滑边界∂Ω的有界区域,∂ν表示单位外法向量的方向导数,边界条件表示它们生活在同一个封闭的环境,常数d1,d2分别是u,v的扩散系数,d2d3是交叉扩散系数,参数α,β,a,b,δ均为正常数。
对于捕食模型,国内外已有许多研究,并且取得了很多有意义的成果,诸如捕食问题正平衡态解的存在性、稳定性和惟一性、局部和全局分歧等。有关这些模型的背景、研究成果和进展,有兴趣的读者可参看文献[1-8]。对于d3=0且功能反应函数为Holling-Tanner型函数的模型,文献[9]利用Lyapunov方法研究了其平衡态正常数解的全局稳定性,文献[10]讨论了其非常数正解的存在性和不存在性。对于d3≠0即带有交叉扩散项的模型,文献[11]讨论了反应函数为Holling-Tanner型函数时模型平衡态正解的先验估计和非常数正解的存在性。但是Holling-Tanner型函数只与变量u有关,这是食物依赖型的反应函数,说明捕食者的捕食行为仅仅由食饵决定,这有悖于一些物种的实际观测结果。因此我们引入较Holling-Tanner更合理的Beddington-DeAngelis功能反应函数来进一步刻画生态系统,研究物种的共存条件。模型(1)对应的平衡态方程为:
(2)
其中d3≥0,记J=-▽(d2v+d2d3uv)=-d2d3v▽u-(d2+d2d3u)▽v,如果d3>0,那么-d2d3v▽u表示大群食饵者避开捕食者的侵害。对模型更详细的生物意义和背景可参看文献[ 4,12-14]。
显然,(2)有惟一的一个正常数解(u*,v*),其中

v*=δu*,(m=a+bδ)
本文主要研究模型(2)非常数正解的存在性。
1 正解的先验估计
为了得到正解的估计,首先引入下面的两个引理。

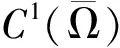
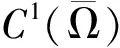

Δw+c(x)w=0,x∈Ω;∂νw=0,x∈∂Ω
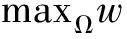


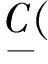

≤,≤
(3)
令w=d2(1+d3u)v,则w(x)满足方程

(4)

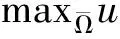
又由于(4)等价于
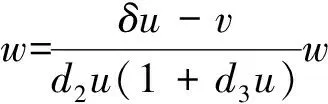
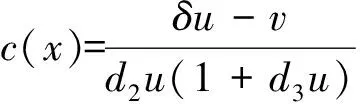



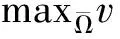
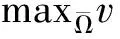
假设u(x),v(x)没有下界,则存在参数列(d1,i,d2,i,d3,i)=(d1,d2,d3),其中d1,i,d2,i≥D1,d3,i≥0,使得模型(2)对应的正解列(ui,vi)满足
→0或者→0,i→∞
(5)
由于(ui,vi)满足方程
(6)
对(6)式两端在Ω上积分得

(7)

2 非常数正解的不存在性
设0=λ0<λ1<λ2<……是-Δ算子在Neumann边界条件下的特征值,其中λi的代数重数记为mi≥1。

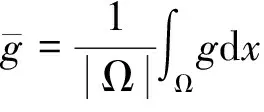
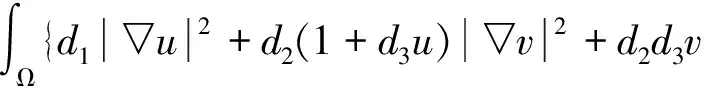

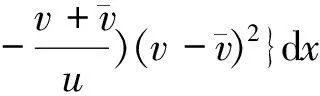
由定理1和ε-Young不等式,有
▽u|2+d2(1 +d3u)|▽v|2]dx≤
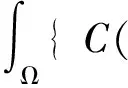

其中C(ε)只依赖于Λ,Ω,ε和D。
≤


3 非常数正解的存在性
令w(d3)=(1+d3u)v,w*(d3)=(1+d3u*)v*,为了方便将w(d3)和w*(d3)分别记为w和w*。令U*=(u*,w*),U=(u,w),那么模型(2)等价于
(I-G)U=0
(8)
其中
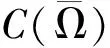
-(I-DUG(U*))(y,z)=μ(y,z),(y,z)≠(0,0)
(9)
由Leray-Schauder度理论知,如果0不是(9)的特征值,那么
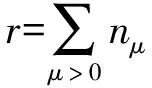
(10)
其中nμ是方程(9)的正特征值的代数重数。显然,方程(9)等价于
-d1(μ+ 1)Δy+
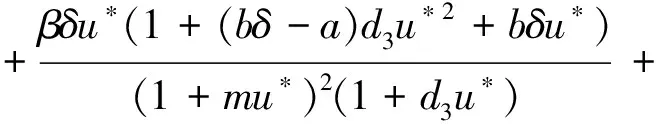
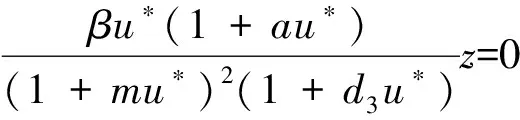
-d2(μ+ 1)Δz+

∂νy=∂νz=0,x∈∂Ω
(11)
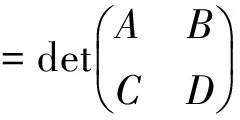

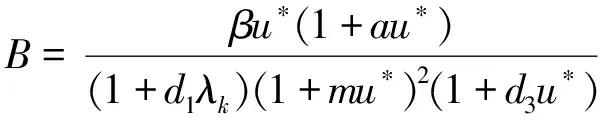

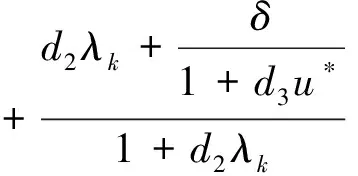
记Pk(μ)=0的正解μ的代数重数为lμ。由(10)式知,对任意的整数k≥0,Pk(0)≠0,那么

(12)
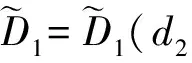
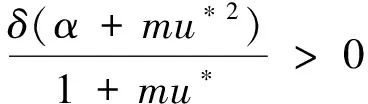
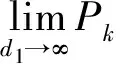

证明记Pk(μ)关于μ的常数项为Π(k),那么直接计算得
Π
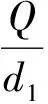
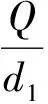
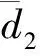
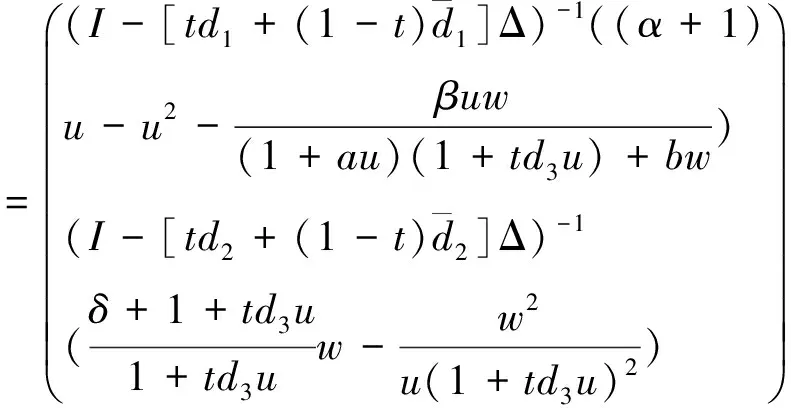


deg(I-G(·;0),Θ,0)=index(G(·;0),U*)=1
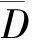
deg(I-G(·;1),Θ,0)=
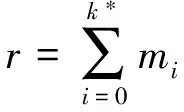
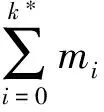
参考文献:
[1]CHEN W Y,PENG R.Stationary patterns created by cross-diffusion for the competitor-competitor-mutualist model [J].J Math Anal Appl,2004,291: 550-564.
[2]DU Y H,LOU Y.S-shaped global bifurcation curve and Hopf bifurcation of positive solutions to a predator-prey model [J].J Differential Equation,1998,144: 390-440.
[3]KUTO K.Stability of steady-state solutions to a prey-predator system with cross-diffusion [J].J Differential Equation,2004,197: 293-314.
[4]KUTO K,YAMADA Y.Multiple coexistence states for a prey-predator system with cross-diffusion [J].J Differential Equation,2004,197:315-348.
[5]LOU Y,NI W M.Diffusion vs cross-diffusion: an elliptic approach [J].J.Differential Equation,1999,154: 157-190.
[6]PANG P Y H,WANG M X.Strategy and stationary pattern in a three-species predator-prey model [J].J Differential Equation,2004,200:245-273.
[7]SCHREIBER S J.Coexistence for species sharing a predator [J].J Differential Equation,2004,196: 209-225.
[8]WANG M X.Non-constant positive steady states of Sel’kov model [J].J Differential Equation,2003,190: 600-620.
[9]PENG R,WANG M X.Global stability of the equilibrium of a diffusive Holling-Tanner prey-predator model [J].Appl Math Lett,2007,20: 664-670.
[10]PENG R,WANG M X.Positive steady states of the Holling-Tanner prey-predator model with diffusion [J].Proc Roy Soc Edinburgh (A),2005,135: 149-164.
[11]PENG R,WANG M X,YANG G Y.Stationary patterns of the Holling-Tanner prey-predator model with diffusion and cross-diffusion [J].Appl Math Comp,2008,196: 570-577.
[12]DUBEY B,DAS B,HASSAIN J.A predator-prey interaction model with self and cross-diffusion [J].Ecol Model,2002,141: 67-76.
[13]NAKASHIMA K,YAMADA Y.Positive steady states for prey-predator models with cross-diffusion [J].Adv Differ Equat,1996,6: 1099-1122.
[14]RYU K,AHN I.Positive steady-states for two interacting species models with linear self-cross diffusions [J].Discrete Contin Dynam Syst,2003,9: 1049-1061.
[15]LOU Y,NI W M.Diffusion,self-diffusion and cross-diffusion [J].J Differential Equation,1996,131:79-131.
[16]LIN C S,NI W M,TAKAGI I.Large amplitude stationary solutions to a chemostat systems [J].J Differential Equation,1988,72: 1-27.
