使用怀特检验判断生物量模型的异方差性
2012-05-08申屠惠良
申屠惠良
(国家林业局华东林业调查规划设计院,浙江 杭州 310019)
使用怀特检验判断生物量模型的异方差性
申屠惠良
(国家林业局华东林业调查规划设计院,浙江 杭州 310019)
为了在生物量建模过程中得到回归模型的最优估计,针对回归模型存在的异方差性,提出用怀特检验方法来定量分析模型,再结合残差分布图来辅助判断,并应用怀特检验方法和残差分布图实例分析了普通最小二乘法拟合栎类生物量模型结果存在异方差性,建议采用加权最小二乘法拟合栎类生物量模型。
生物量;模型;怀特检验;异方差性
生物量建模过程中,要求模型的误差项必须满足零数学期望、独立和等方差,这样才能得到回归模型的最优估计,而误差项的方差经常会随着自变量的变化,产生规律性的增加或减少,即不满足等方差,也就是回归模型存在异方差性。如何判断建立的回归模型存在异方差性,本文采用怀特检验方法来定量分析模型,再结合残差分布图来辅助判断。
1 怀特检验的原理
生物量模型表达式为:

式中,M表示生物量,D为胸径,H为树高,V为材积,a、b为常数。
怀特检验是通过建立辅助回归模型的方式来判断异方差性,在生物量建模应用过程中设定如下辅助回归模型:

式中,E2为残差平方,ai为辅助回归模型的参数,υ为满足古典回归模型基本假设的误差项。
怀特检验辅助回归模型的原理是,将残差平方与胸径、树高、材积的一次项、二次项和交叉乘积项建立回归方程,拟合产生回归模型的参数项和误差项,再根据建立的辅助回归模型计算残差平方的拟合值,分析残差平方的原始值和拟合值之间存在的关系,可以判断回归模型的异方差性。
假定辅助回归模型的R2值在零假设条件下不存在异方差性,也就是辅助回归模型的回归结果不存在异方差性,则R2与样本容量的乘积服从分布。在生物量建模应用过程中,设定上侧分位数置信区间为“0.05”,即α = 0.05,且自由度为3,当nR2大于上侧分位数值,说明生物量模型存在异方差性,也就是回归模型不满足“独立、正态、等方差”的基本假设。
2 残差分布图判别法
3 实例分析
生物量建模数据,按样本的部位可以分解为树干、树枝、树叶和树根,各部位可以单独建立回归模型,在实例分析中采用2010年采集的栎类数据,且将样本各部位生物量数据组合成为一个总体,使用怀特检验和残差图判别法来验证回归模型的异方差性。
3.1 怀特检验
原始采集的生物量建模数据因天气、样本所在的地理位置等原因,部分样本不符合建模要求,称为扰动数据。剔除扰动数据以后,实际样本数量n =52,自由度为p = 3个,分别是D、H和V,使用回归模型表达式为式(1),经普通最小二乘法拟合,结果见表1。

表1 普通最小二乘法拟合结果Table 1 Fitting statistics by ordinary least squares
由此可以建立栎类总体生物量的回归方程:
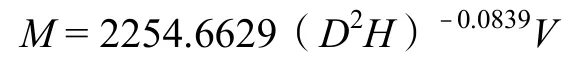

表2 怀特辅助回归模型拟合结果Table 2 Fitting statistics by associated regression model

式中,Q为辅助回归模型的残差平方和,U为辅助回归模型的离差平方和。
由此获得的计算结果如表3。

表3 怀特检验结果Table 3 White test
栎类总体生物量数据如果使用普通最小二乘法进行拟合,从怀特检验结果表中可以看出,nR2值大于上侧分位数(xα2),回归模型存在异方差性,也就是说,回归模型拟合结果不是最优解,需要将模型进行变换,采用加权最小二乘法进行估计,消除异方差性。
3.2 残差分布图
回归模型是否存在异方差性,也可以从残差平方分布图中判断。按普通最小二乘法回归后获得栎类总体生物量样本的拟合值()和残差平方值(),将拟合值()作为X轴,残差平方值()为Y轴,绘制残差平方分布图(图1)。
从残差平方分布图中可以看出散点的分布成发散趋势,残差平方随拟合值有显著变化,说明普通最小二乘法拟合结果存在异方差性,和怀特检验的定量分析是一致的。
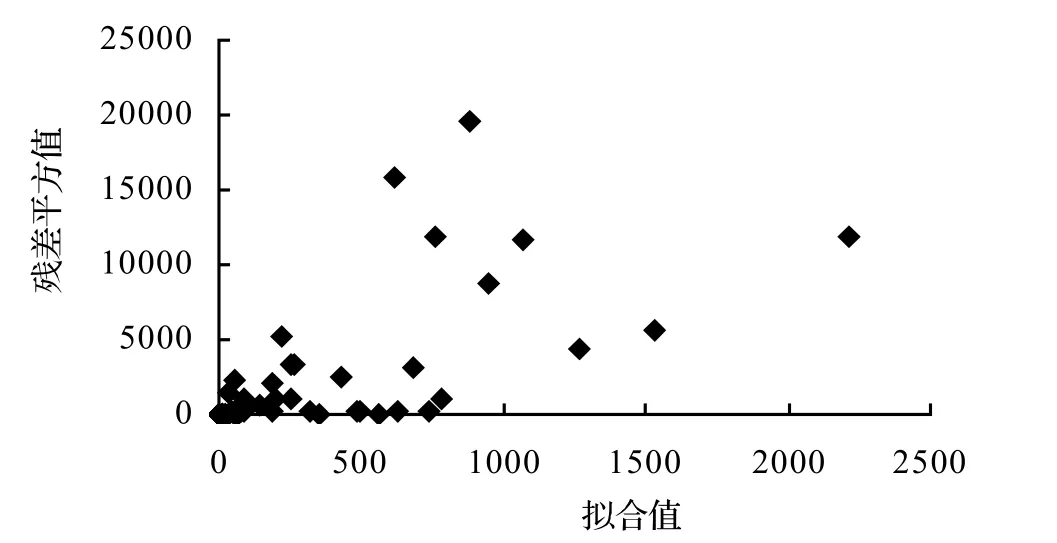
图1 生物量残差平方分布Figure 1 Residuals distribution
[1] 唐守正. 多元统计分析方法[M]. 中国林业出版社,1984.
[2] 张会儒,唐守正,胥辉. 关于生物量模型中的异方差问题[J]. 林业资源管理,1999(1):46-49.
[3] 彭伟,陈圣滔. 回归模型中异方差的检验方法[J]. 钦州学院学报,2007,22(6):29-31, 42.
White Test for Heteroskedasticity of Biomass Model
SHENTU Hui-liang
(East China Forest Inventory and Planning Institute of State Forestry Administration, Hangzhou 310019, China)
In order to have the optimal estimation during regression model for biomass, White test was recommended to quantitative analyze model, associated by residuals distribution. Application of White test and residuals was conducted on analysis of biomass model for Quercus L. fitted by ordinary least squares, the result showed that there had heteroskedasticity. Therefore, weighted least squares were recommended to fit biomass model for Quercus L.
biomass; model; white test; heteroskedasticity
S718.55+6
A
1001-3776(2012)03-0043-03
2011-11-15;
2012-03-03
申屠惠良(1960-),男,浙江东阳人,工程师,从事林业调查规划设计相关的林业技术研究。
