智能算法中粒子群优化研究和实现

张雁，肖伟

摘要：粒子群优化(PSO)算法是一种新颖的演化算法,它属于一类随机全局优化技术,通过粒子间的相互作用在复杂搜索空间中发现最优区域。该文介绍了PSO算法的基本原理、应用领域，并用matlab实现了该过程。

关键词：粒子群算法优化应用；智能算法；编程语言matlab

中图分类号：TP311文献标识码：A文章编号：009-3044(2012)02-0429-03

1导论

有优化作用的粒子群算法是主要应用在计算智能领域中。相比早期的智能算法如经典的蚁群算法和鱼群算法等，它又是又一类群体智能的优化算法。该算法最早由Kennedy和Eberhart在1995年提出的。该算法的灵感来源于对鸟类捕食行为的研究。我们观察在鸟类捕食时，对所有鸟来说，找到食物最有效、简单的的数据信息就是由当前距离食物最近的周围区域的鸟群提供。粒子群算法就从这种生物种群行为特征受到启发并借鉴应用于求解优化问题的。在算法中可知优化问题每次的潜在存在的解集合都是由搜索空间中假定的“粒子”的状态决定，每个粒子的适应度值由目标函数决定的，它们飞翔的方向和距离由粒子的速度决定了。粒子由自身及同群同伙伴的飞行经验协调性地且动态地调整进行，即粒子自己单个个体具备的最优解和整个种群所具备的最优解。如此反复在解空间中不断搜索，如遇满足要求停止。本测试用例就是用PSO算法来求标准测试函数的极值，表明该算法在系统极值寻优中的有效作用。

2原理

可以视为第i个粒子的周围附近粒子所能得到的最优位置，上述方法也有“局部PSO算法”的提法。比较而言，全局PSO算法收敛快，数值在局部最优附近容易聚集。相反局部PSO收敛速度会慢一点，但不易走入局部最优。

3算法实现

3.1算法流程

①群算法参数初始化，群体规模，每个粒子的位置xi和速度,Vi

②对应计算每个粒子的适应度值Fit[i]；

③对应于每个粒子，比较它的适应度值和个体极值，如存在Fit [i]> pbes (i),则用Fit [i]替换掉pbes (i);

④对应于每个粒子，比较它的适应度值Fit[i]和全局极值gbes(i),如存在Fit [i]> pbes (i)则用Fit [i]代替gbes(i)；

⑤根据公式（1），（2）更新替换粒子的速度xi和位置Vi；

⑥如遇结束条件满足退出(误差足够好或到达最大循环次数)，否则重复步骤②。

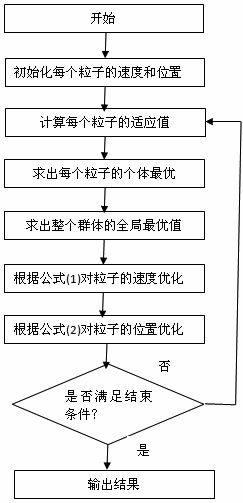
图1 PSO算法流程图

3.3实现结果

在本实验中，采用matlab实现该算法，如下是算法的显示结果：

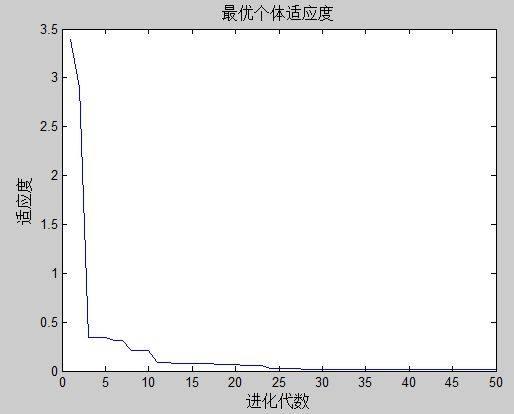
图2 PSO实现结果（c1=0,c2=4）

4应用

PSO算法简易实现,没有太多参数需要调整,且不需要可微可导信息和与之相关的此类的信息。PSO可作为连续优化和混合整数非线性问题和排列组合优化问题的优化方法[2]。PSO早期应用于诸如神经等网络初步训练上，稍后PSO进一步可以用来确定在神经网络中的实质结构。如今广泛应用于在神经网络训练为后的函数优化、模糊性系统控制与其他智能算法的应用领域。

4.1函数优化

粒子群算法原理与收敛性的研究都是为了更好研究和解决函数的优化问题，通常象这一类问题都是相当复杂的，问题特征表现为规模之大、维数之高、数学性质上可体现为非线性、非凸和不可微等微积性质，大量极小局部存在函数分布里。相对早期的传统的优化确定性算法解决这类问题速度较快，反应灵敏度高，初值的选择上体现出相应的的要求，局部特性上可见易陷入局部最小。提到另外具有优化全局性的算法，如智能遗传算法、退火模拟算法、进化规划等，它们各自的不同的机理和结构单一，难以实现在高维复杂函数等方向上的高效优化。但PSO算法综合这些优缺点，实现高效优化对复杂高维函数的作用。

4.2神经网络的训练

PSO算法现在主要是在训练神经网络的3个大的方面（网络几何拓扑结构及函数传递、连接时权重的设置、智能学习采用算法）。每个粒子可完整勾勒表达出神经网络的相关的所有参数，反复更新来实现对这些参数的优化，由此达到训练的功效。相比同类型的学习算法如误差反向传播算法，使用粒子群算法在神经网络的方面的优点在于不借助于可微可导等微分性质，进而使用一些不可微的在函数之间传递信息。大概率情况下所能得到的结果比误差反向传播算法要好，速度也更快些。

4.3参数优化

粒子群算法选用在连续的各类问题和离散的各类问题的参数优化。目前有信号处理机器人路径规划、模糊控制器的设计和模式识别等问题

4.4组合优化

由“01”串的编码方式实现的粒子群算法在许多组合优化问题中有序结构的表达问题以及约束条件处理问题等上尚需有更合理的解决方案和措施。所以问题的不同，提相应问题的特定粒子表达方式不同，也可以通过重新定义算子来解决。已解决了多种TSP、VRP以及车间调度等问题的优化方案。

5结束语

粒子群算法是新型的群体智能的进化算法,其研究也开始兴起,远没有像遗传算法和模拟退火算法稳健发展，有一定的系统的分析方法和一定的数学基础,许多问题要进一步地分析，给出方法。

可喜的是目前我国大量学者在对PSO算法的适用性和方法性的研究上有了新的研究动态[4],能让粒子群算法能在更多优化研究工作上带来更多的新的启发和思路。

参考文献：

[1] Kennedy J , Eberhart R C. Particle Swarm Optlmization. Proc[R].IEEE Int ,Lconf.on Neural Networks. IEBE Service Center, Pisca-taway , NJ ,1995 (4) :1942-1948.

[2] Eberhart R,Kennedy J.A New Optimizer Using Particle Swarm Theory[C].In:Proc of the Sixth International Symposium on Micro Machine and Human Science,Nagoya,Japan,1995:39-43.

[3] Richards M, Ventura D. Choosing a starting configuration for particle swarm optimization [A]. in: Proc. IEEE Int. Joint. Conf. Neural Net? work [C],2004(3):2309–2312.

[4]何妮,吴燕仙.粒子群优化算法的研究[J]科技信息,2008(6):179-220.

[5]王万良,唐宇.微粒群算法的研究现状与展望[J].浙江工业大学学报,2007,35(2):136-141.

[6 ]谢晓锋,张文俊,杨之廉.微粒群算法综述[J].控制与决策,2003,18(2):129-134.

[7]徐海,刘石,马勇,等.基于改进粒子群游优化的模糊逻辑系统自学习算法[J].计算机工程与应用,2000 (7):62- 63.