有理数运算法则教学体会
2012-04-29陈富金
陈富金
摘要 在现实生活中会遇到许多实际问题,比如温度的上升或下降,收入的增加或减少等,这些都是引入负数的实际需要,也是学习更高段数学内容的需要。因此,加深对有理数的认识,是为学习有理数的运算作准备。
关键词 有理数;运算法则;教学
有理数的运算是初等数学的基本运算,掌握有理数的运算是学好后续内容的重要前提,因此,学生要加强对有理数运算法则的理解,特别是会用法则进行运算,并应用有理数运算法则解决实际问题。
七年级数学起始阶段有两个主要任务,一是扩展数域,引进负数,建立有理数集;二是通过用字母表示数,建立代数式,为从数的运算过渡到式的运算奠定基础。可见,《有理数》和《代数初步知识》两部分在初中代数中的地位和作用。然而,代数式的加减法运算又完全依赖于有理数的运算,而有理数的运算又源于其法则,所以说,有理数的运算法则是代数运算的基础中的基础。因此,教师讲授有理数法则效果的好与差,将直接影响到学生今后的学习。
对于有理数的运算,简单地说,就是“判别类型,运用法则”。对于有理数的几种运算类型,学生比较容易区分,而有理数的几个运算法则,学生容易混淆。因此,为了使学生透彻地理解法则,正确地运用法则,在进行有理数法则的教学中,我在历届的教学活动中都作了如下两点尝试:
第一,借助負数的意义,通过日常生活中的具体事例,帮助学生理解运算法则中符号的确定。
我们知道,任何一个有理数(0除外)都是由它的符号和绝对值两部分构成的,有理数的四则运算与小学中的四则运算根本的区别就在于运算结果的符号。因此,如何确定运算结果的符号,是有理数法则教学的重点和难点,为了使学生理解法则中符号的确定,先通过日常生活中的实例,说明正数和负数的意义,使学生对“+”号和“-”号有一个感性认识,然后通过归纳、总结,导出法则,使学生形成理性认识。
在有理数加法法则的教学中,首先向学生提出一个这样的问题:甲、乙两队进行拔河比赛,当你不在场的时候,你凭什么来判断哪个队赢呢?这样一问,学生给愣住了,稍后,一位学生回答:“哪个队的拉力大就哪个队赢”。教师说:“这位同学回答得非常正确,把问题说到点子上”。紧接着把话题一转:“若设甲队的拉力为正向拉力,乙队的拉力为负向拉力,若正向拉力大于负向拉力,绳子就向甲队移动,移动到规定距离,就甲他赢;反之就是乙队赢”。在此基础上,教师进一步引导学生把上面的感性认识转化为理性认识,讲解:“我们用一个正数来表示甲队的拉力,用一个负数来表示乙队的拉,在两队拉力的共同作用下,绳子移动的结果就是一个正数与一个负数的和,绳子移动的方向就是这个和的符号,移动的距离就是和的绝对值;当绳子向甲队方向移动时,说明这个和是一个正数,当绳子向乙队方向移动时,说明这个和是一个负数。可见,和(包括它的符号和绝对值)是由两队拉力(即正、负数的绝对值)的大小确定的”。这样,学生就不难得出有理数运算法则中的“异号两数相加,取绝对值较大的加数的符号,用较大的绝对值减去较小的绝对值”。
第二,利用图表,帮助学生比较、区分法则。
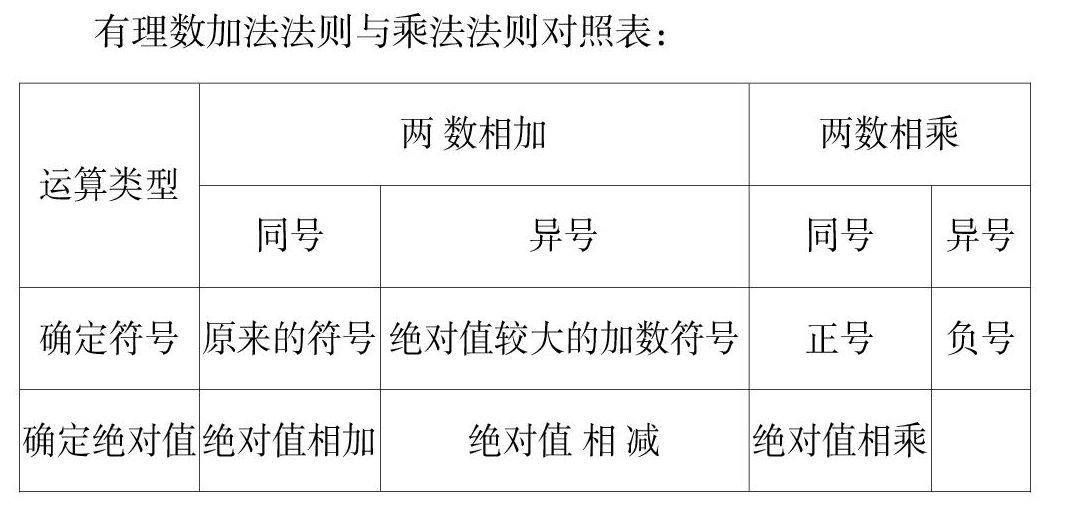
有理数的四则运算法则中,主要是加法法则和乘法法则,学生对两个法则的符号容易混淆,对异号两数相加时,把绝对值相加还是相减,有时还分不清,且对法则的内容也不易记忆。因此,在单元小结中,将这两个法则演绎成下表,以帮助学生辨认和区分。
有理数加法法则与乘法法则对照表:
上面的对照表,既体现出两个法则中运算结果的符号的确定和绝对值的确定,又能把两个法则加以比较对照,这对学生记忆、区分法则很有帮助。
同时,教师应注重培养学生良好的运算习惯,以减少不必要的失误。如不少学生在运算时由于贪快或粗心,当结果是负数时,往往漏掉结果中的负号,针对这一问题,教师强调学生要把每一步运算分成两步进行:一是先定符号;二是再定绝对值。书写时,如果结果是负数,应先写上符号,再计算绝对值。
运用上面的方法进行有理数法则教学,对学生理解法则、运用法则指导计算很有帮助,会收到事半功倍的效果。
