主副拱协作体系柔性系杆拱桥拱肋刚度优化
2012-04-26石雪飞
石雪飞, 徐 凯
(同济大学桥梁工程系,上海 200092)
0 引言
主副拱协作体系(斜靠式)柔性系杆拱桥外形独特新颖、造型美观,富有曲线美和力度感,在城市桥型特别是宽桥桥型的选择中具有明显的优势[1]。该桥型无风撑横梁,拱肋是由主拱和斜靠的副拱构成的组合拱,是一种受力复杂的空间组合体系,除了具有一般拱桥的受力特点以外,还具有明显有空间效应。
目前对斜靠式拱桥结构体系的研究还不多。文献[2]结合昆山玉峰大桥对大跨度无推力斜靠式拱桥的设计进行了概述。文献[3]对斜靠式拱桥主拱和斜拱的施工做了介绍。文献[4]对斜靠式拱桥主副拱刚度参数进行了分析,并探讨了刚度比对结构稳定的影响。文献[5]对影响内力的参数,如矢跨比和拱梁刚度以及影响稳定性的参数,如斜拱倾角、横撑数量、横撑刚度及位置等进行了相关研究。
上述研究的背景桥梁结构形式为刚梁刚拱梁拱协作受力体系,且未提出刚度比优化目标,没有确定性结论。研究对象为主副拱协作体系柔性系杆拱桥。桥面横梁由主副拱肋的4根吊杆共同吊起,可视为倒置的弹性地基梁。桥面荷载首先作用于桥面板后传递至横梁,再由吊杆传力至拱肋。本文确定了拱肋刚度优化目标,实现了主副拱协作体系柔性系杆拱桥拱肋刚度的优化。
1 桥梁概况
该桥由双提篮系杆拱及两侧边孔V型刚构组成,主桥跨径120m。刚构的斜腿与基础固结,对应的主副拱肋在拱脚处通过刚构横梁与边孔V型刚构固结,拱和边孔刚构形成稳定的整体结构体系。全桥设两片拱肋,每片拱肋由主、副拱肋各一肢组成。主拱肋位于铅直面内,副拱肋位于与铅直面夹角为9°的斜平面内。主拱肋处设系杆平衡拱的水平力,整个组合拱桥为无水平推力的自平衡结构。结构布置见图1。
本桥采用四片拱肋共同受力,每个横梁设置主、副共四根吊杆,与一般系杆拱桥两片拱肋有较大区别,需要对主副拱肋进行优化。
2 优化目标及优化参数
优化目标:在满足结构强度、刚度及稳定性条件下,调整主、副拱截面大小,当主、副拱控制截面在荷载作用下的内力与主、副拱控制截面抗力对应成比例,材料的利用率达到最大,则认为此时主、副拱截面是合理的。__________

图1 背景桥梁三视图
优化时保持矢跨比、拱肋线型不变,主副拱肋的刚度仅由主副拱肋的截面控制。故本文对主副拱体系的优化即是对主副拱截面的优化。
优化截面采用与原截面相同的截面形式,是原截面放大(或缩小)后的截面。原截面形式和尺寸如图2所示。现定义优化截面和原截面高度比值为截面放大系数,记作α。主拱截面放大系数为α1,副拱截面放大系数为α2。
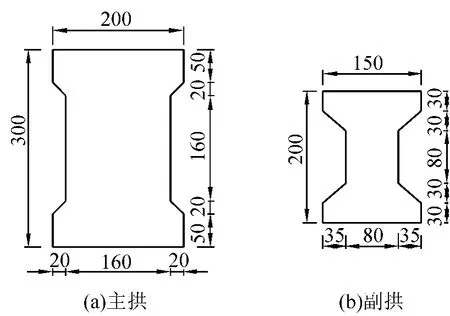
图2 原设计主、副拱截面尺寸(单位:cm)
3 优化参数计算
拱肋所受荷载主要包括:①施工阶段荷载,包括拱肋自重和横梁自重;②成桥阶段荷载,包括二期恒载和活荷载。
拱肋所受荷载作用,除了拱肋自重效应,均由吊杆传递至拱肋结构。用拱肋结构的某一控制截面的内力反映整个拱肋结构随主副拱肋截面变化的受力状态,应保证所选取的控制截面及控制内力具有代表性。经计算分析,选定拱顶截面为控制截面,拱顶截面弯矩为控制内力,以反应主副拱肋截面参数发生变化时拱肋内力效应的变化情况。
3.1 拱肋自重作用下优化参数计算
主副拱肋均为无铰拱,是变截面超静定结构。当拱肋截面发生变化时,结构的刚度也随之变化。对变截面超静定结构,刚度的变化又会影响其内力分布情况。通过不断调整主拱截面放大系数α1和副拱截面放大系数α2,获得自重荷载作用下主、副拱拱肋拱顶截面弯矩随截面放大系数的变化情况。由于拱肋的自重效应与其截面大小成正比,即与截面放大系数的平方α2成正比,故通过二次多项式拟合数据点,获得主副拱拱顶截面弯矩的表达式。
拱肋自重作用下,主、副拱截面弯矩随主拱截面放大系数α1及副拱截面放大系数α2变化情况如表1、表2所示。
根据表1、表2数据,绘出主拱拱顶弯矩随主拱截面放大系数α1及副拱截面放大系数α2变化图,并进行曲线拟合,如图3、图4所示。
据此获得拱肋自重作用下主副拱拱顶弯矩的参数表达式
主拱
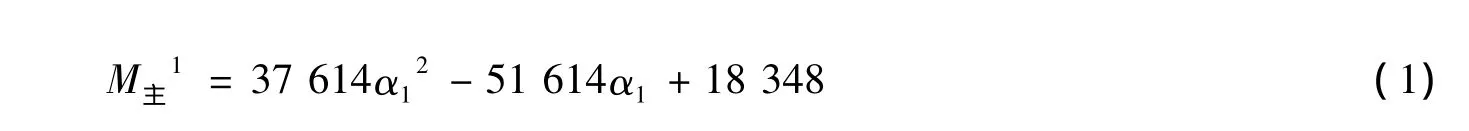
副拱

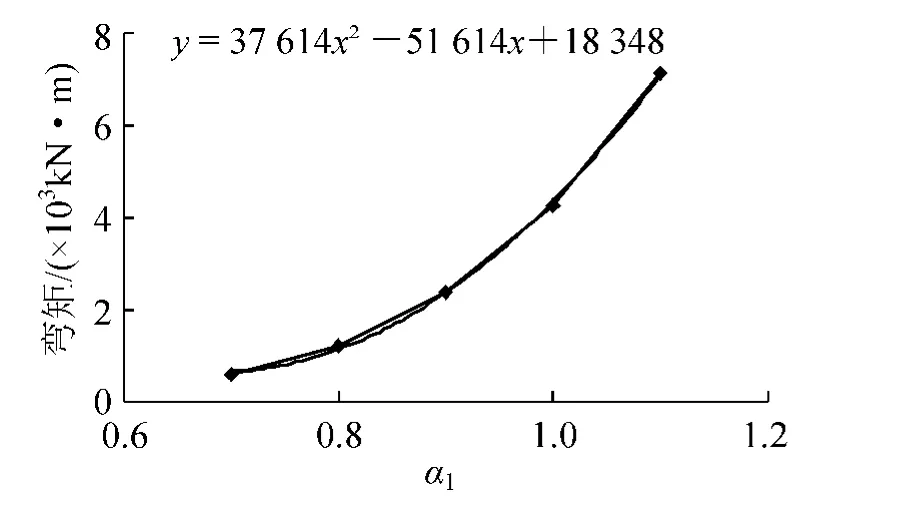
图3 拱肋自重作用下主拱拱顶弯矩随α1变化图

图4 拱肋自重作用下副拱拱顶弯矩随α2变化图

表1 拱肋自重作用下主、副拱截面弯矩随α1变化表
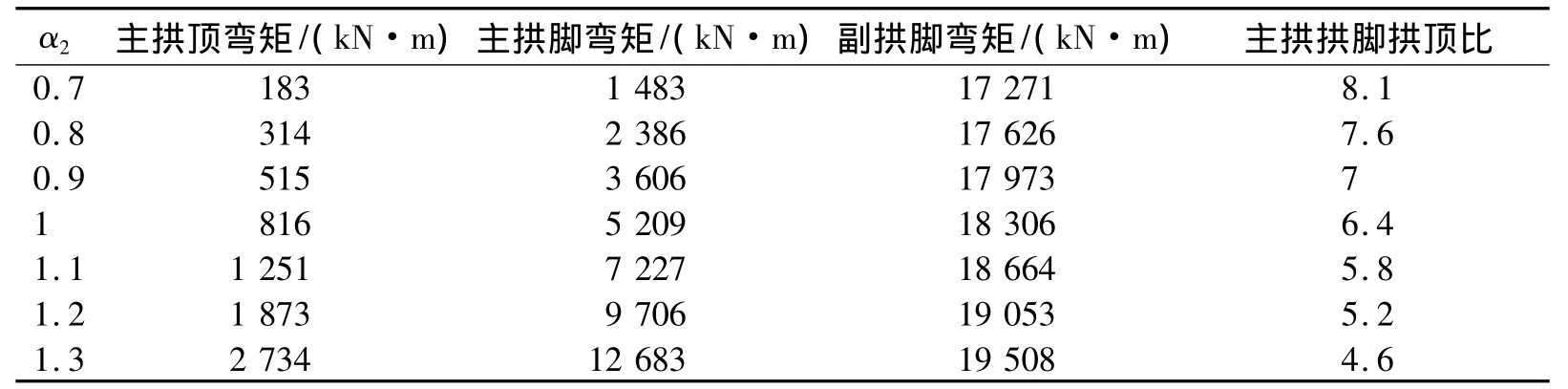
表2 拱肋自重作用下主、副拱截面弯矩随α2变化表
3.2 横梁自重作用下优化参数计算
采用与拱肋自重荷载相同的分析方法,通过不断调整主拱截面放大系数α1和副拱截面放大系数α2,获得横梁自重荷载作用下主、副拱拱肋拱顶截面弯矩随截面放大系数的变化情况,并通过多项式拟合数据点,获得主副拱拱顶截面弯矩的表达式。
横梁自重荷载作用下,主、副拱截面弯矩随主拱截面放大系数α1及副拱截面放大系数α2变化情况如表3、表4所示。
根据上表数据,绘出主拱拱顶弯矩随主拱截面放大系数及副拱截面放大系数变化图,并进行曲线拟合,如图5、图6所示。
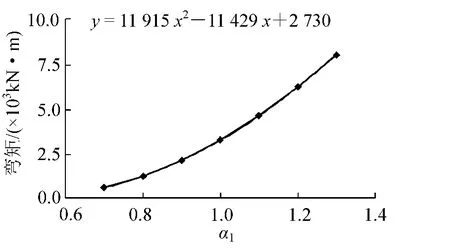
图5 横梁自重作用下主拱拱顶弯矩随α1变化图

图6 横梁自重作用下副拱拱顶弯矩随α2变化图
据此获得横梁自重荷载作用下主副拱拱顶弯矩的参数表达式
主拱

副拱

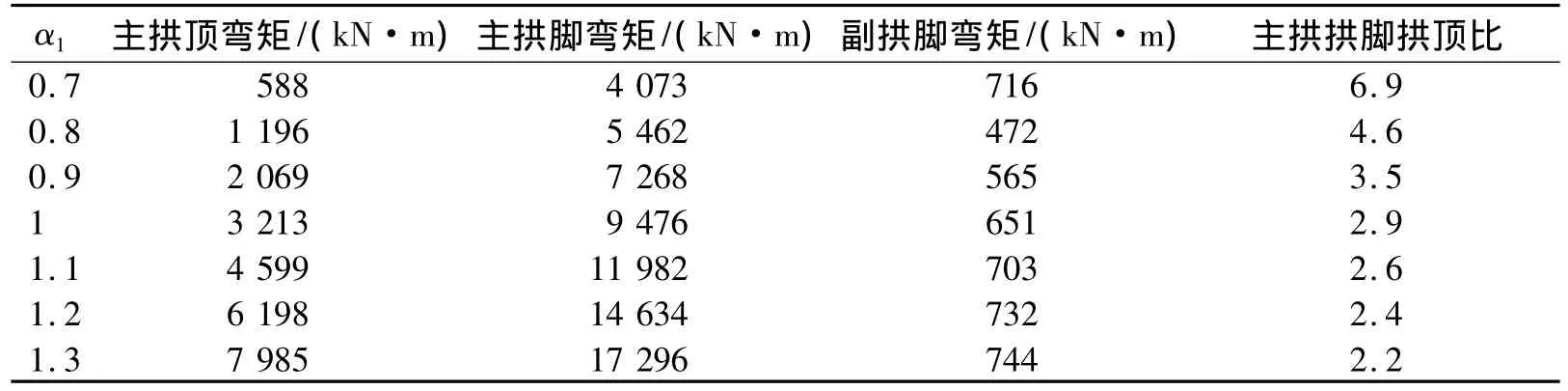
表3 横梁自重作用下主、副拱截面弯矩随α1变化表

表4 横梁自重作用下主、副拱截面弯矩随α2变化表
3.3 成桥阶段荷载参数计算
为简化计算,成桥阶段活荷载仅考虑车道荷载和人群荷载,并将其效应值换算成均布荷载作用于横梁上。车道荷载按双向6车道全桥满布布置,并考虑多车道横向和纵向折减。车道荷载集中力分摊至各片横梁。人群荷载根据人行道布置,计算其总的荷载效应后,换算成均布荷载作用于横梁。荷载效应值按正常使用极限状态长期效应组合采用。
成桥阶段荷载作用于横梁,通过主副吊杆力最终作用于主副拱肋。前面式(3)、式(4)计算了横梁自重效应的参数表达式。成桥荷载与横梁自重都通过主副吊杆传力至拱肋,故可参考横梁自重效应的参数表达式,推导出成桥阶段荷载的参数表达式。
原设计方案中,横梁自重引起的主拱吊杆力为570 kN,副拱吊杆力为190 kN。成桥荷载引起的主副拱吊杆力分别为814.4 kN和164.1 kN。据此获得成桥阶段吊杆力荷载作用下主副拱拱顶弯矩的参数表达式
主拱
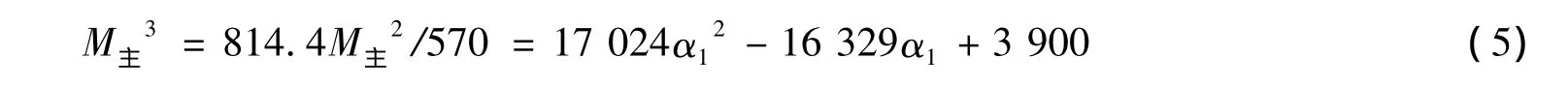
副拱

3.4 截面抗力参数计算
原设计主、副拱截面为钢筋混凝土截面,其截面抗弯承载力可用截面抗弯模量表示。截面抗弯模量与截面放大系数α3成正比。主拱截面惯性矩为I=4.3 m4,梁高为ymax=1.5m;副拱截面惯性矩为I=0.92 m4,梁高为ymax=1.0m。则有主副拱抗力为
主拱
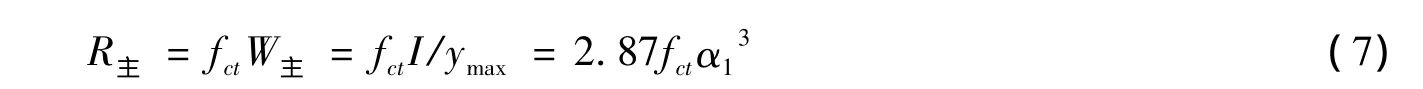
副拱

4 截面参数优化计算及结果
主副拱肋截面的优化目标为:调整主副拱截面大小,使得主、副拱控制截面内力在荷载作用下与主、副拱控制截面抗力对应成比例,此时主、副拱截面比例是合理的。据此列出优化方程式

代入上述各参数表达式,得到α1、α2关系式。运用Matlab得到α1、α2在可行域内的关系曲线,见图7。
从图7可以得出满足优化目标的主、副拱截面放大系数对应关系。当副拱截面放大系数采用原设计截面,即副拱截面放大系数为1.0时,对应的主拱截面放大系数为0.8。故优化方案主拱截面放大系数取0.8,副拱截面放大系数取 1.0。
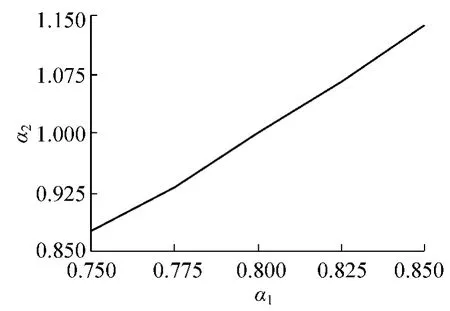
图7 主、副拱截面放大系数关系曲线
5 优化方案与原设计方案对比
有限元模型计算得到原设计方案和优化方案主副拱截面效应和抗力见表5。
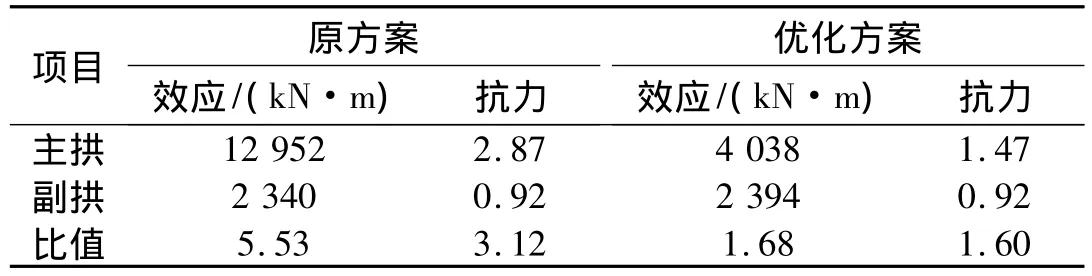
表5 原设计方案与优化方案对比
可见,效应与抗力的比值由原设计方案的1.78变为1.05,约等于1,优化目标实现。优化后的方案,拱肋截面受力合理,混凝土材料得到了充分利用。
6 结论
以主、副拱控制截面在荷载作用下内力与主、副拱控制截面抗力对应成比例为优化原则下对主副拱肋截面进行了优化。研究发现,当副拱截面采用原设计截面,主拱截面放大系数取0.8时可以实现上述优化目标,使拱肋截面受力合理,混凝土材料充分利用,该主副拱协作体系柔性系杆拱桥拱肋截面得到优化。需要注意的是:为简化计算,成桥阶段活荷载仅考虑车道荷载和人群荷载,并将其效应换算成均布荷载作用于横梁上。在实际活载作用下拱肋的受力情况会有所不同。提出的优化方法可用于类似桥梁结构初步设计时截面优化。
[1]肖汝诚,孙海涛,贾丽君,等.斜靠式拱桥[J].上海公路,2004(4):22-26.
[2]肖汝诚,孙海涛,贾丽君,等.昆山玉峰大桥——首座大跨度无推力斜靠式拱桥的设计研究[J].土木工程学报,2005,38(1):78-83.
[3]潘寿东.斜靠式系杆拱桥主、斜拱圈安装施工技术[J].石家庄铁道学院学报,2006,19(1):122-127.
[4]阳霞.斜靠式拱桥结构体系与稳定性分析[D].长沙:中南大学土木工程学院,2011.
[5]李莹.斜靠式梁拱组合体系桥梁设计理论研究[D].上海:同济大学土木工程学院,2006.
