一种OFDM系统中叠加导频的信道估计方法

段 鹏

(中国电子科技集团公司第20研究所通信事业部，陕西西安 710068)

由于传输速率高和抗多径干扰等特点，OFDM技术近年来已在各个系统中得到广泛应用。信道估计作为其关键技术在传输质量中起到至关重要的作用。目前，由于其不占用带宽的传输特点，基于叠加导频的信道估计方法得到了广泛的关注。此方法在插入导频估计［1－2］、半盲估计［3］和盲估计［4］中都得到一定的研究和应用。文献［5］提出，在发送端首先利用导频序列与发送数据进行相关运算，将相关性最小的导频叠加到数据上发送。文献［6］中提出了利用接收序列的一阶统计特性将导频序列与未知数据分离进行信道估计的方法。但现有的方法总是不能将未知数据与导频完全分离，即导频中除有噪声干扰外还伴有未知数据的干扰。

提出了一种新的信道估计方法:利用 Mounir Ghogho等人提出的利用循环导频序列经过FFT变换后，能量集中在频域中某些频点上的特点［7］，将叠加导频从接收数据中完全分离出来，并利用PN序列在时域中进行信道估计。由于此方法利用PN序列的自相关性，所以在低信噪比时性能显著，通过仿真及与传统方法进行了比较，并进一步分析了参数的设置与信道估计的MSE之间的关系。

1 信道模型的建立

OFDM的收发系统如图1所示，在发送端数据首先进行QPSK调制，再经过串并转换，将叠加导频序列插入数据中进行IFFT变换，最后加上循环前缀(CP)送至中频。数据经过多径时变信道后到达接收端，接收数据首先去掉循环前缀，然后进行FFT变换，在频域进行信道估计与均衡，也可以在时域进行信道估计与均衡。设发送端信号的离散表达式为

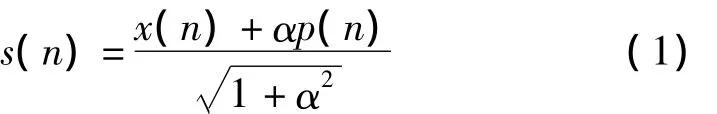
式中，x(n)表示要发送的未知数据;p(n)表示导频序列;s(n)表示叠加后的发送数据;α表示功率分配的比例系数，以保证设离散多径时变信道模型为 h=［h(0)，h(1)，…，h(L－1)］，其中L为信道总路径数，经过多径信道并加上高斯白噪声干扰，则接收信号表示为

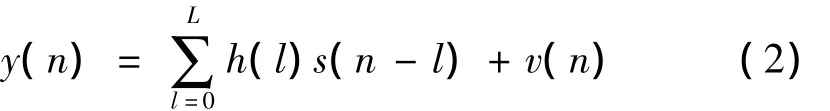
式中，y(n)表示接收信号;h(l)为多径信道;v(n)为高斯白噪声。由式(1)可进一步得到接收信号的表达式

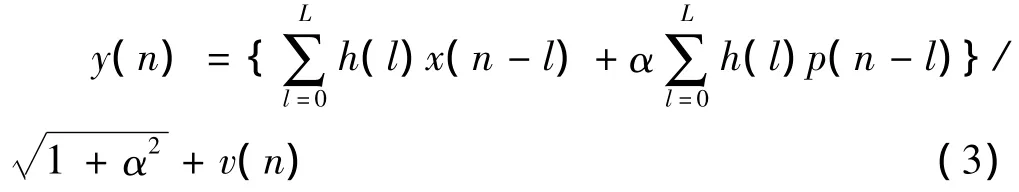
在广义平稳非相关散射(WSSUS)信道模型下，信道的自相关函数为［8，10］

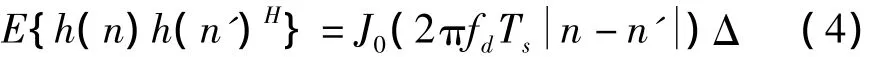
式中，J0(·)表示零阶贝塞尔函数;fd为最大多谱勒频移;Ts表示采样周期;Δ 表示 diag(，…，);diag(·)表示对角矩阵。

图1 OFDM收发系统的原理框图

2 叠加导频信道估计方法

2.1 方案的提出

将接收端的信号去除掉循环前缀后进行FFT转换，得到频域表达式

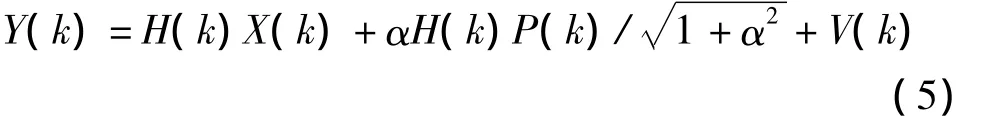
根据Mounir Ghogho提出的理论，如果p(n)使用循环序列，那么在频域中P(k)的能量只集中在p(n)序列周期的整倍数频点上。设子载波个数为N;p(n)的周期为P，D=N/P，且D为整数，那么p(n)的能量只集中在频点 k=qD 上，q=0，1，2，…，P －1，其余各频点的值均为零。如果将未知发送数据在时域中进行简单的线性变换，可以使其在频域中某些点为零。这样在频域中就相当于将导频插入到未知数据为零的某些频点上，这些频点上的数据只与导频有关不受未知数据的干扰。由于分离出来的导频信号只在某些频点上有值，无法在频域中直接均衡，同时估计的信道参数受到噪声的干扰较大，尤其是在低信噪比情况下。

文献［9］提出利用PN码进行时域信道估计，可以大幅降低噪声对导频的影响，并且计算复杂度较低，但这种方法需要插入导频序列进行估计，降低了系统的带宽利用率。

根据上述方法，提出一种利用循环PN码作为叠加导频在时域进行信道估计的方法。

2.2 新的信道估计方法

由于在发送端将导频信号设计成循环PN序列，那么此序列在频域中也具备Mounir Ghogho序列的特性。本文所选用的PN序列为m序列，其自相关性可表示如下

导频序列设计为 p(n)=［W，W，…，W］，其中 W=［m(0)，m(1)，…，m(P)］，此序列共有 D=N/P 个 W，这样序列既具有循环特性又具备PN码的自相关特性。利用文献［8］中对未知发送数据进行处理，设

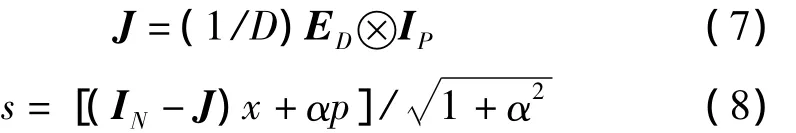
这里ED表示D阶全1矩阵;IP和IN分别表示P阶和N阶单位阵;⊗表示Kronecker乘积;s，x，p分别表示忽略时间参数的发送序列、未知数据序列和导频序列。如果设，则式(8)可改写成

则此时的S已经具备Mounir Ghogho序列的特性。在接收端，将接收到的信号去除循环前缀后，进行FFT变换得到Y(k)，再将导频序列不为零的频点取出组成新的序列

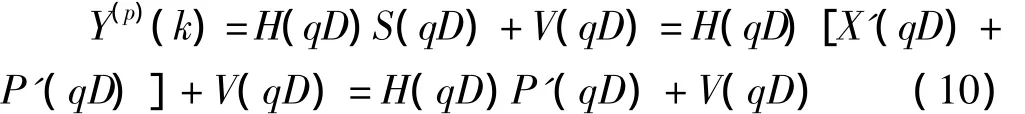
式(10)中，Y(p)(k)即在接收序列Y(k)里每隔D－1个元素取出后组成的新序列，由于数据序列在频点qD，q=0，1，2，…，P －1 上等于零，所以 Y(p)(k)只与导频序列有关而不受未知数据干扰，并对此序列进行P=N/D点IFFT变换得到式(11)

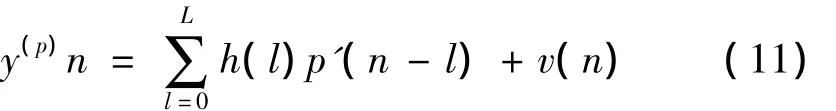
式中，v(n)为经过IFFT变换后的噪声序列。由式(11)可以看出，经过IFFT变换后的Y(p)(n)，相当于一个PN序列不叠加未知数据经过信道后的接收序列。

将得到的时域数据与由PN序列组成的循环行列式 Ψ进行相乘，再左乘得到信道的估计值

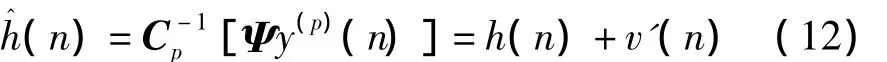
式(12)中，Ψ 为一个的方阵，且 Ψ =［W，W(1)，…，W(P)］T，W为一个m序列，W(j)为将W向右循环移位j个单位的向量;Cp为P×P的方阵，其主对角线为P，其余值为－1。v'(n)=Ψv(n)，由于噪声序列与PN序列的相关性很小，所以相关运算后的噪声功率相比于信道估计参数功率降低为1/P。最后将估计出的时域参数再经FFT后转化到频域进行信道均衡。

2.3 计算复杂度分析

所提出方法的复杂度主要由式(12)决定，可以看出，要计算(n)需要进行2P2次乘法运算。虽然要计算Cp的逆，但是此矩阵是一个固定矩阵，在接收端可以提前计算好，这样可以大大降低计算量。

3 系统仿真与结果分析

针对OFDM系统中叠加导频的信道的特性，采用新的信道估计方法，在Jack［10］信道模型下进行计算机仿真。信号幅度衰落服从瑞利分布特性，相位服从均匀分布。载波频率为2 GHz，子载波间隔为7.5 kHz，最大多谱勒频移fd=250 Hz和fd=150 Hz，多径个数为5条，各径幅度的衰落由R=exp(－τdi/τav)表示，τdi表示各径的时延，τav表示平均时延。仿真的子载波个数 N 分别为 128、256、512、1024、2048，循环前缀CP=32，基带数字调制选用QPSK，PN序列选用m序列。D选为4，则 P为 N/4。这里信道估计的均方误差(MSE)由式(13)计算。

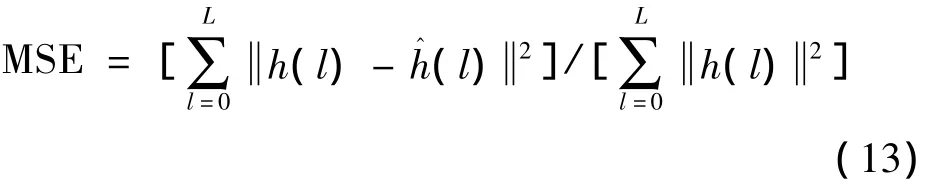
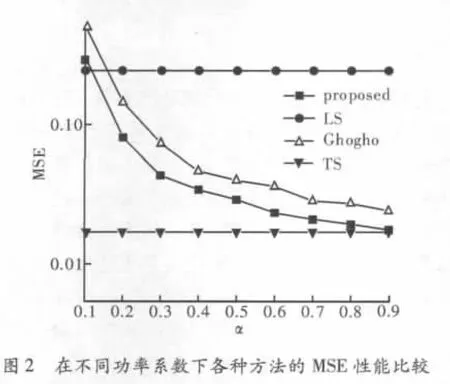
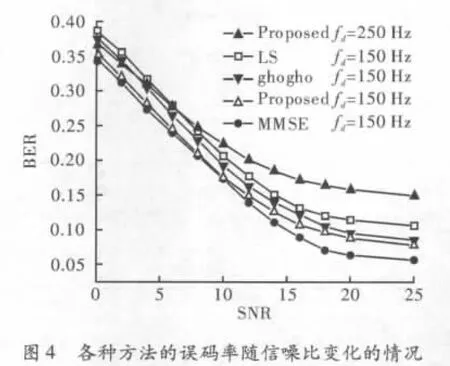
图2显示了在SNR=6 dB，fd=150 Hz时，各种方法信道估计的MSE随功率分配系数变化的曲线。从图中可以看出建议方法的性能随功率分配系数增大而提升，并最终接近于TS方法，这意味着此方法可以将导频完全从接收数据中分离出来。图3表示在不同子载波个数的情况下信道估计的MSE随信噪比变化的情况。可以看出在信噪比较低时子载波个数较大的MSE性能较为突出，这是由于m序列的周期长，相对降低噪声干扰的能力强［9］，反之在高信噪比时，性能与较少子载波个数的情况相近。图4，图5分别表示新方法和传统方法的误码率和信道估计的MSE比较结果。其中Ghogho指Mounir Ghogho所提方法在时域补零后在频域进行均衡的信道估计结果。其中子载波个数 N=256，α =0.5，fd=150 Hz和 fd=250 Hz。可以看出在fd=150 Hz时，在低信噪比情况下，建议方法与MMSE的性能相近，并好于LS、Ghogho的性能。但在fd=250 Hz时，此方法在高信噪比时性能随信噪比变化不明显，曲线趋于平坦。

4 结束语

提出了一种结合周期导频和PN序列特点的基于叠加导频的信道估计方法。由于周期性导频经FFT变换后，能量集中在某些点上，因此可以将其从接收数据中完全分离出来，而不受传输数据影响。利用PN序列自相关性的特点在时域进行信道估计能够进一步降低噪声对导频的干扰。实验结果表明所提出的新方法有如下优点:(1)不占用传输带宽，有较高的频谱利用率。(2)可以将导频较为干净地从接收数据中分离出来，尤其是在低信噪比时性能更为优越。(3)BER和MSE的性能优于传统叠加导频方法。(4)计算复杂度较低。

［1］ EDFORS O，SANDELL M，VAN DE BEEK J J，et al.OFDM channel estimation by singular value decomposition ［J］.IEEE Trans on Communications，1998，46(7):931 －939.

［2］ MA X，GIANNAKIS G，OHNO S.Optimal training for block transmissions over doubly － selective fading channels［J］.IEEE Transsctions on Signal Processing，2003，51(5):1351－1366.

［3］ CAI X，AKANSU A N.A Subspace method for blind channel identification in OFDM systems［C］.New Orleans，LA:Proc.ICC，2000:929 －933.

［4］ MUQUET B，DE COURVILLE M，DUHANMEL P.Subspace－based blind and semi_blind channel estimation for OFDM systems［J］.IEEE Trans on Signal Processing，2002，50(7):1699－1712.

［5］ TSUZUKI F，OHTSUKI T.Channel estimation with selective superimposed polit sequences under fast fading environments［J］.ICIEC Trans on Communications，2006，E89 － B(2):556－563.

［6］ TUGNAIT J K，LUO W L.On channel estimation using superimposed training ans first order statistics［J］.IEEE Communications Letters，2003，7(9):413 －415.

［7］ GHOGHO M，MCLEMON D，HEMANDEZ E A，et al.Channel transmission using data－dependent superimposed training ［J］.IEEE Signal Processing Letters，2005(12):226－229.

［8］ YANG Qinghai，KYUNG SUP KWAK，FU Fenglin.Superimposed training for estimation doubly－selective OFDM channels［C］.USA CA:CAC，2007:12 －14.

［9］ XU Guoping，WEI Qun，ZHANG Xin，et al.New OFDM channel estimation algorithm with low complexity［C］.2007 IEEE 65th Vehicular Technology Conference－VTC2007－Spring，2007:2257 －2260.

［10］ JAKES W C.Microwave mobile communications［M］.New York:Wiley Press，1974.