曲面片的可展切曲面及其映射分析

毛 昕， 杨静林， 马明旭

（东北大学机械工程与自动化学院，辽宁 沈阳 110004）

曲面片的可展切曲面及其映射分析

毛 昕， 杨静林， 马明旭

（东北大学机械工程与自动化学院，辽宁 沈阳 110004）

论文以微分几何可展曲面理论为基础，提出了过曲面曲线构造其可展切曲面的方法，得出了可展切曲面的表达形式，对可展切曲面进行了分类，通过建立两曲面间的映射关系，实现了它们间整体与局部的映射分析，较准确地把握曲面的变形情况，并通过实例对方法进行了验证。曲面片可展切曲面的方法可以应用于曲面设计、曲面近似展开和纹理映射等方面。

几何计算；可展切曲面；曲面映射；变形分析

可展曲面在工程中有着广泛的应用，可展曲面的构造与逼近近年来得到广泛和深入的研究[1~6]。在曲面结构设计中，经常遇到过曲面上一条曲线设计与该曲面相切曲面的情况，若相切曲面为可展曲面，会给加工制造带来方便。在不可展曲面近似展开时，往往用可展曲面对其进行局部置换，若可展曲面与不可展曲面有很好的接近程度，便会提高近似展开的精度。另外在近似展开的误差分析、纹理映射的变形控制等场合，还需要建立两块曲面间的映射分析，掌握变形情况。文献[7-9]在回转曲面近似展开的误差分析中，利用回转曲面的可展切柱面进行展开并分析展开误差。在此基础上，本文提出了过曲面上曲线构造其可展切曲面的一般性方法，得出了可展切曲面的表达形式，并通过建立两曲面间的映射关系，实现了它们间的映射分析。

1 可展切曲面的构造

1.1 过曲面曲线的可展切曲面

如图1所示，曲面Σ的方程为：r =r( u,v)，Σ上的任意曲线Γ对应参数 u = u(t),v =v(t)，其方程为 r =r (u (t),v(t) ) =r( t )。在Γ曲线上任意点t处，Σ有确定的切平面 St；随参数t的变化，沿曲线Γ形成一个切平面族

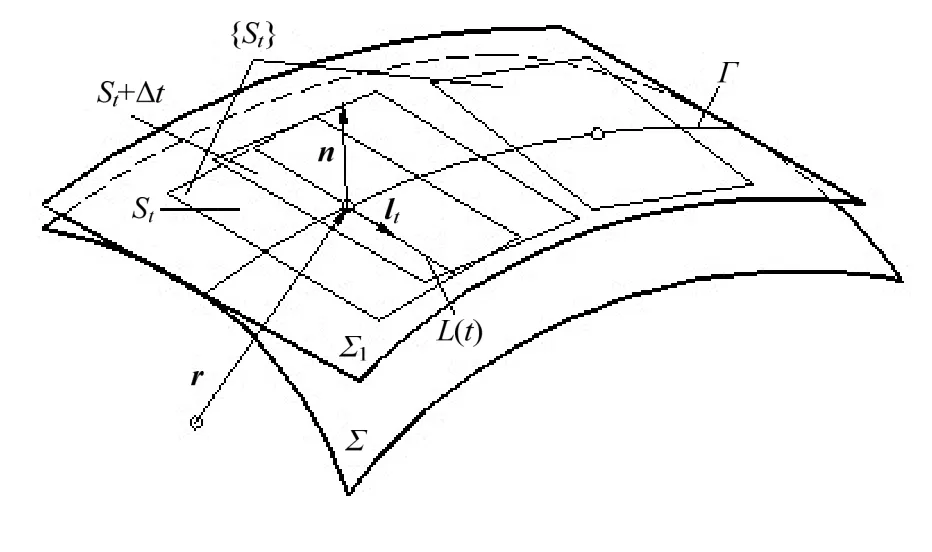
图1 曲面片及其可展切曲面

式中： n( t)为Σ在t处的单位法矢，R为Σ在t处的切平面矢量， p(t)为原点到该切平面的距离。一般地，{St}非平行面族和共轴面族，于是{St}存在一个包络曲面 Σ1。因为 Σ1上的点同时必为{St}中某个平面上的点，即 Σ1上的点均满足式（1）。对式（1）取微分有(R ⋅n′(t) −p′(t)) dt+ n( t)⋅ d( R) =0，因为 n(t)⋅ d (R) = 0, dt ≠0，所以(R ⋅n′ (t) − p′(t)) =0，于是 Σ1上的点应同时满足

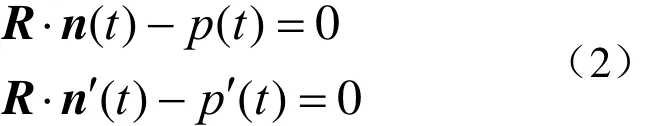
从式（2）中消去参数 t，即得曲面 Σ1。下面证明 Σ1为直纹可展曲面。

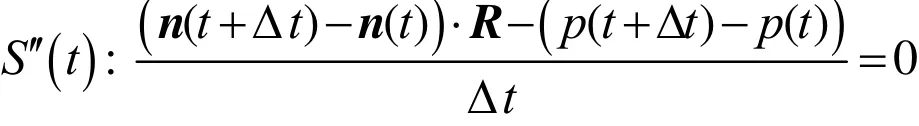
在{St}中取平面 St:n(t) ⋅ R − p(t) =0和St+Δt:n (t +Δt ) ⋅ R − p(t +Δt )=0，两平面相交于一条直线，显然这条直线也在平面上。当 Δ t→ 0，平面 St′′→ St′ : n ′(t)⋅R−p′(t) = 0，这时，相交直线趋向它的极限位置Lt， Lt称为{St}在 St上的特征线。因为 Lt满足式（2），所以 Lt⊂ Σ1；又因为 Lt在 St上，所以St沿 Lt与 Σ1相切。由连续性可知，Σ1是单参数特征线族{Lt}的集合，即 Σ1是直纹曲面， Lt是Σ1的直素线。

设沿特征线 Lt方向的单位矢量为 l( t)（见图2），这时， Σ1的方程可写为

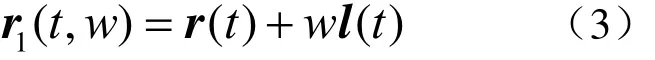
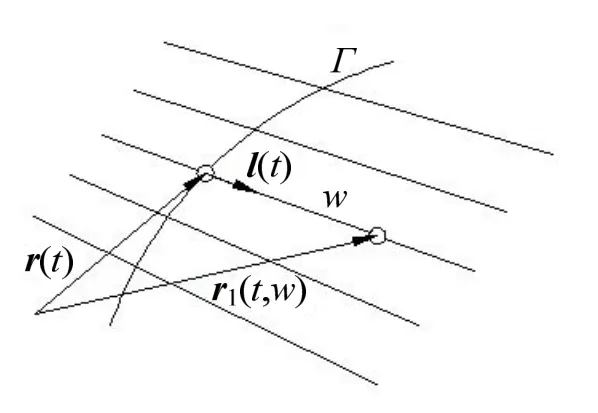
图2 可展切曲面的表达

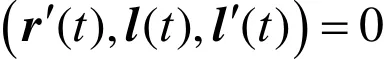
即 Σ1为可展曲面[10]。

由前面可知 Σ1的法矢为 n (t,w ) =(r′(t)+ wl′ (t) )× l( t)，且其方向不随w的值而改变。又由于(r ′ (t) ,l( t) ,l′ (t )) =0，所以 l′ (t)、 r′(t)和l( t)三矢量共面且均在切平面 St内，因此在Γ曲线上任意参数t处，曲面Σ和 Σ1的法矢共线，即具有公共的切平面，因而Σ和 Σ1两曲面沿Γ曲线相切。

于是，对于曲面Σ，沿其上任意曲线Γ:r = r (u(t),v(t) ) =r( t)，存在一可展曲面 Σ1沿曲线Γ与Σ相切，称 Σ1为Σ的可展切曲面。

1.2 可展切曲面的表达与分类

对于曲面 r =r( u,v)，沿其上曲线Γ（ u = u(t),v = v(t) ,r =r( t)），可展切曲面 Σ1可直接用式（3）来求取，式中

即

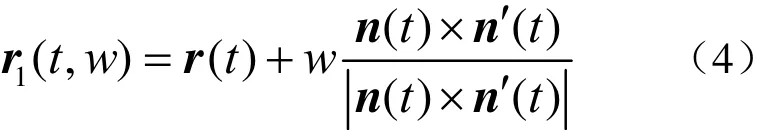
曲面 Σ1的种类可用直素线方向的单位矢量 l( t)的情况来划分。当 lt为常矢量时，Σ1一般为柱面，特殊地，若 r( t)为平面曲线，且 lt在曲线平面内，或 r( t)为直线， lt不与 r( t)同向，这时 Σ1为平面；若 r( t)为直线，且 lt与 r( t)同向，这时，{St}为过 r( t)的面束，Σ1退化为与 r( t)共线的直线。当 lt不是常矢量时，若 lt交于一点，总存在过该点的常矢量 r，使 r1(t,w)= r +wl( t)，这时， Σ1为锥面；若 lt不交于一点，则存在数量函数 λ( t)，使 l( t) =λ (t)r′(t)，即 lt为 r( t)在t处的切矢，这时，Σ1为切线曲面，r(t)即为切线曲面的脊线。

2 可展切曲面与原曲面间的映射与分析

2.1 曲面间的映射

应用中有时要建立可展切曲面1Σ 与原曲面Σ间的映射关系并分析两曲面间的变形情况。图3中，Σ上的点A对应1Σ 上的点A1，如果这种对应是一一的和连续的，便确定了相应的映射关系。为便于分析，可以通过参数变换使两曲面定义在相同的参数域上，得到曲面对 (,)uvr 和1(,)uvr 或 (,)twr 和1(,)twr 。参数间的函数关系一般要根据映射点间的几何关系求得，曲面采用不同的参数域会有不同的参数曲线。

图3 曲面片与其可展切曲面间的映射

2.2 映射分析

2.2.1 整体映射分析

整体映射分析从整体上度量两曲面间几何要素的相对变化情况。

1） 相对参数曲线长度变化

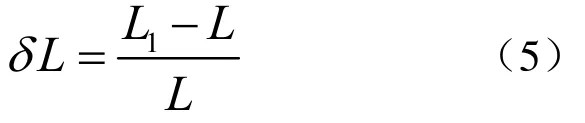
式中，L和1L分别为曲面Σ和1Σ 上对应参数曲线的长度。

2） 相对面积变化

式中，S和1S分别为曲面Σ和1Σ 上对应区域的面积。

3） 相对参数曲线交角变化

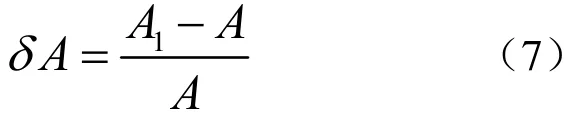
式中，A和1A分别为曲面Σ和1Σ 上对应参数曲线的交角。

2.2.2 局部映射分析

局部映射分析通过度量一对对应点在对应方向上微分长度的变化，来更深入地揭示两曲面间的变形情况。首先引入长度比的概念

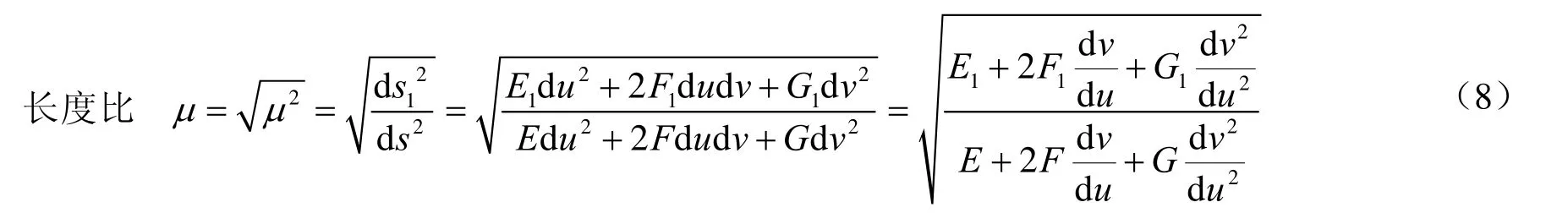
式中，ds和1ds分别为曲面Σ和1Σ 在对应点处的微分弧长，E、F、G和E1、F1、G1分别为两曲面的第1基本量，由上式可见，长度比是曲面上点(u, v)和切方向d/dv u的函数，它的值反映了该点、该方向上微分长度的变化。

1） 极值变换曲线 指曲面映射中长度变化取极值的曲线，该曲线上任意点的切矢方向是该点处长度比取极值的方向。

这是关于极值切方向d/dv u的一元二次方程，解之有

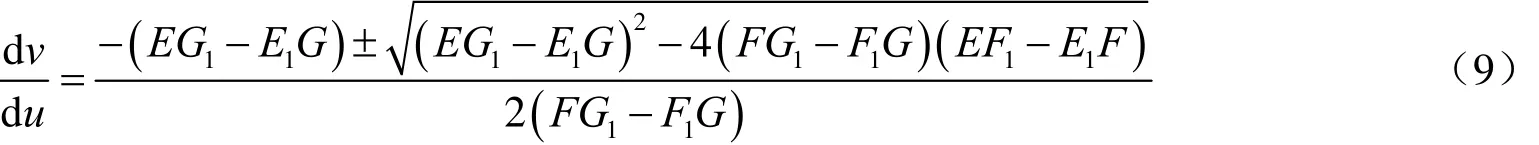
上式即为极值变换曲线的微分方程式，两族解分别对应最大和最小变形曲线。

2） 等距变换曲线 指曲面映射中长度没有变化的曲线，该曲线上任意点的切矢方向是该点处长度比等于1的方向。在式（8）中令 1μ=并整理有

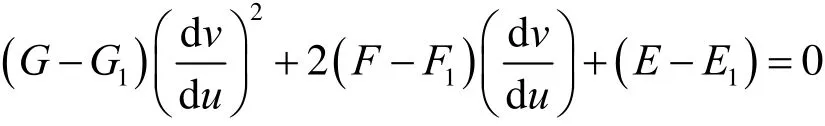
这是关于等距方向d/dv u的一元二次方程，解之有

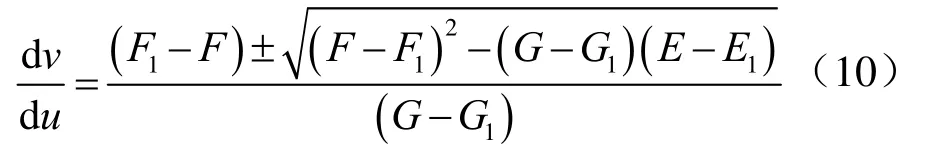
上式即为等距变换曲线的微分方程式，两族解分别对应两族等长变换曲线。下面以双曲抛物面为例说明其可展切曲面的构造及映射分析。

3 应用举例

3.1 双曲抛物面的可展切曲面

双曲抛物面的方程

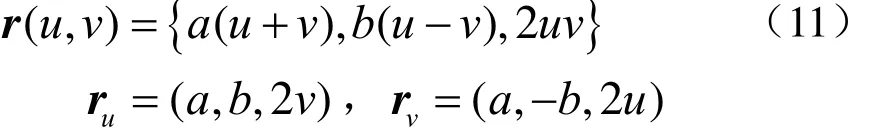
取 Γ 曲线为 y= 0的截线，这时有b(u − v) = 0,即 u = v，令 u = t,v = t，并代入双曲抛物面的方程，可得该截线的方程：r(t) ={2 at, 0,2t2}，该截线为在xoz平面内且经过原点的抛物线。将 u = t,v = t代入法矢公式有

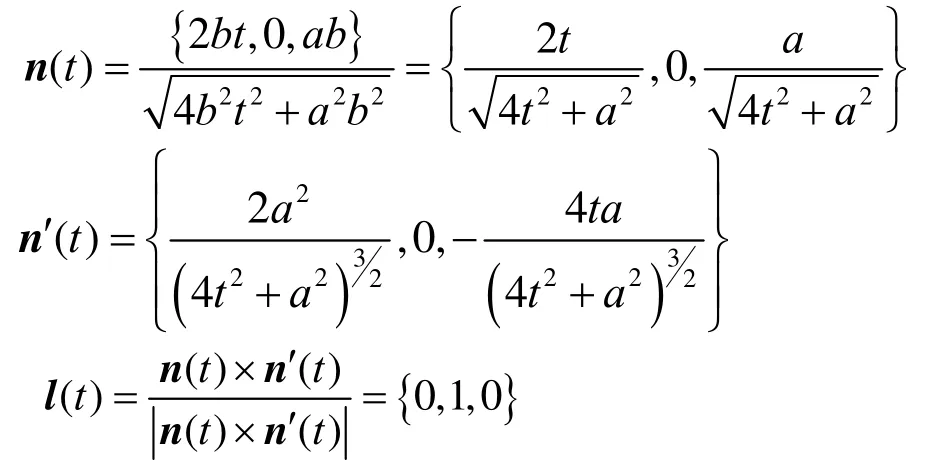
由于 l( t)为常矢量（y方向的单位矢量），所以，可展切曲面为过抛物线 r (t) ={2 at, 0,2t2}，且母线与y轴平行的抛物柱面，具体地

3.2 双曲抛物面与其可展切曲面间的映射分析

3.2.1 建立映射关系

映射时，设双曲抛物面上的点A沿z轴方向映射到抛物柱面上点A1， A和A1具有相同的x和 y坐标，根据式（11）和式（12）有a(u + v) = 2 at,b(u - v) = w ，从中可解出将其代入式（11），得到以 ,tw为参数的双曲抛物面方程

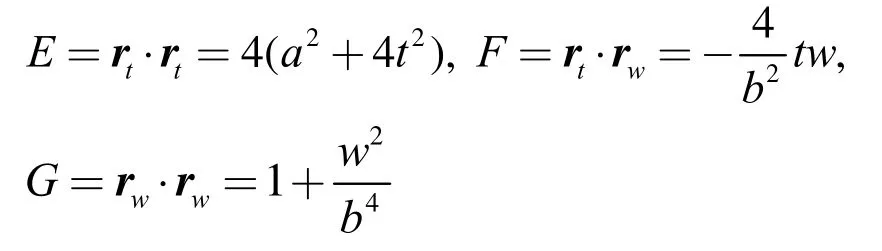
由式（12），可得抛物柱面的第1基本量r1t={2 a,0,4 t } ,r1w={0,1,0}

3.2.2 映射分析

1） t曲线长度的相对变化

对于t曲线有

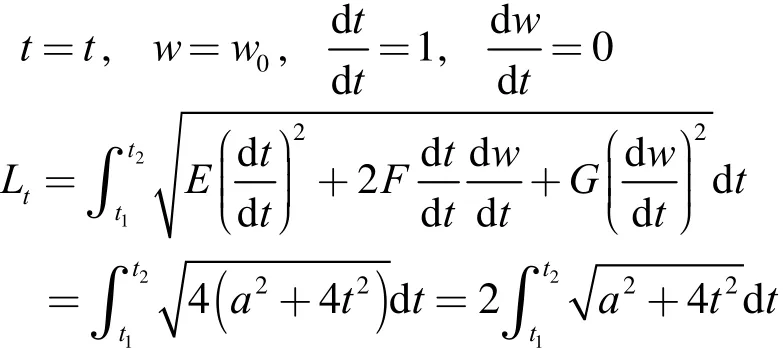
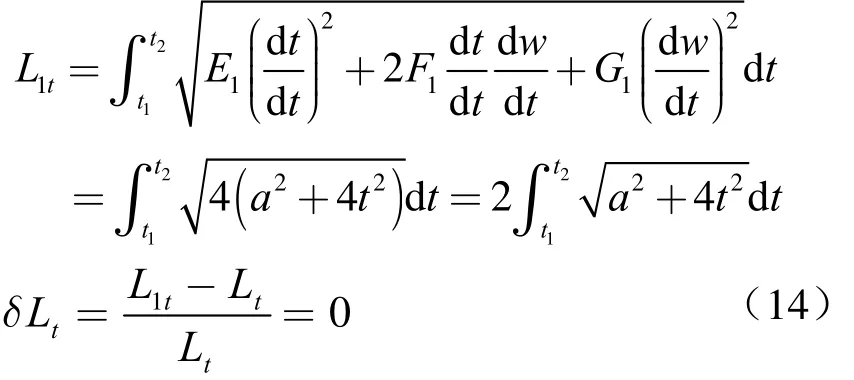
可见，t曲线相对长度的变化为零，即两曲面对应的t曲线具有相同的长度。

2） w曲线长度的相对变化

对于w曲线有

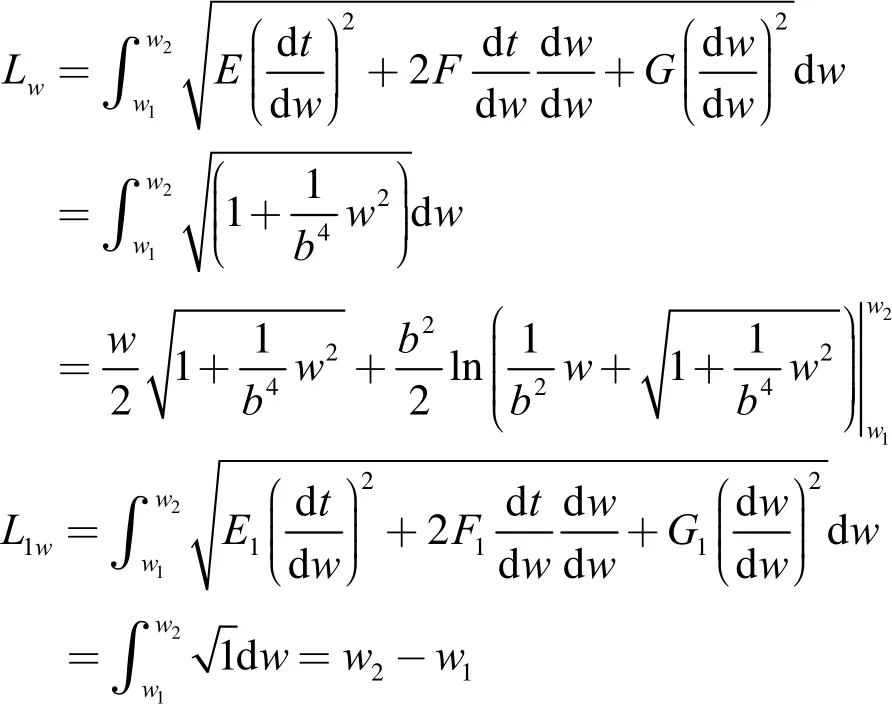
式（15）为w曲线相对长度变化的表达式，图 4为相对长度变化曲线（ a = 3,b = 2，w1= 0,w2= w ）。由图4可见，随着w的增加，w曲线的相对长度变化迅速增大。

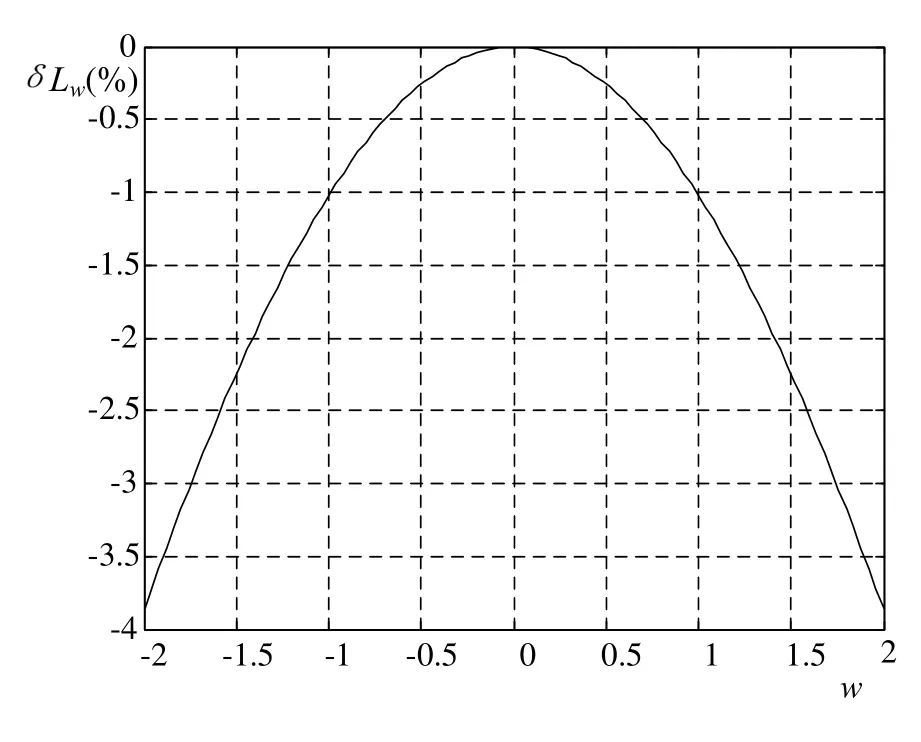
图4 w参数曲线相对长度变化

3） 对应区域面积的相对变化

式（16）是对应区域面积相对变化的表达式，图 5是对于区域 t1= 0,t2= t;w1= 0,w2=w的面积相对变化情况（ a = 3,b = 2），由图5可见，参数t对相对面积变化影响较小，而参数w则影响较大。

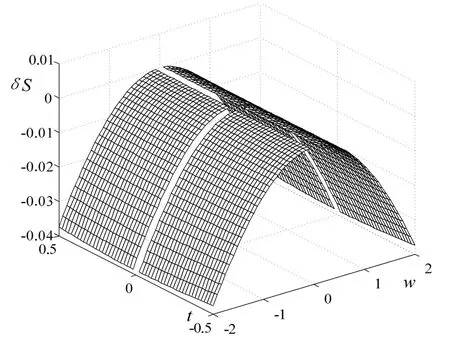
图5 对应区域面积的相对变化

4） 参数曲线交角的相对变化

对于抛物柱面，因为10F= ，所以1/2 A π=对于双曲抛物面有

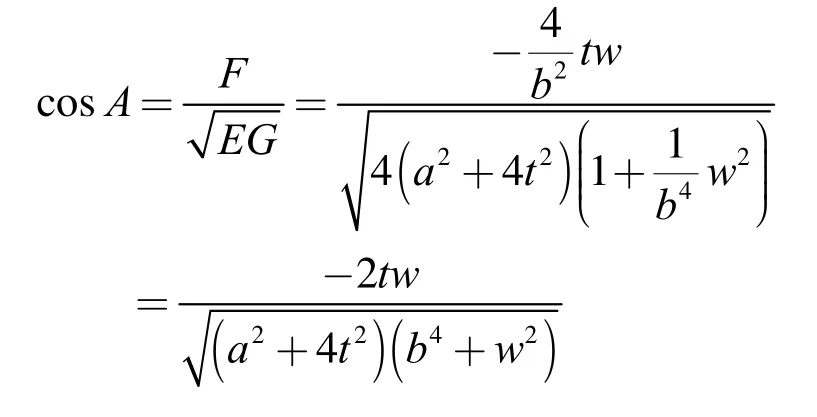
式（17）是参数曲线交角相对变化的表达式，显然，对于Γ曲线：因 为w =0, 所以有δA= 0。图 6是参数曲线交角的相对变化曲线（ a = 3,b = 2），图6中显示，参数曲线交点离原点越远，交角相对变化越大，且变化值相对于曲面原点呈中心对称分布。

5） 极值变换曲线

由式（9）有

图6 参数曲线交角的相对变化

解此微分方程，可得两族极值变换曲线。图7是过点 t= 0.5， w=−5 ,−4 ,… ,5的极值变换曲线，其中一条变形取最大值，另一条取最小值。图8是极值变换曲线在双曲抛物面上的映射结果。

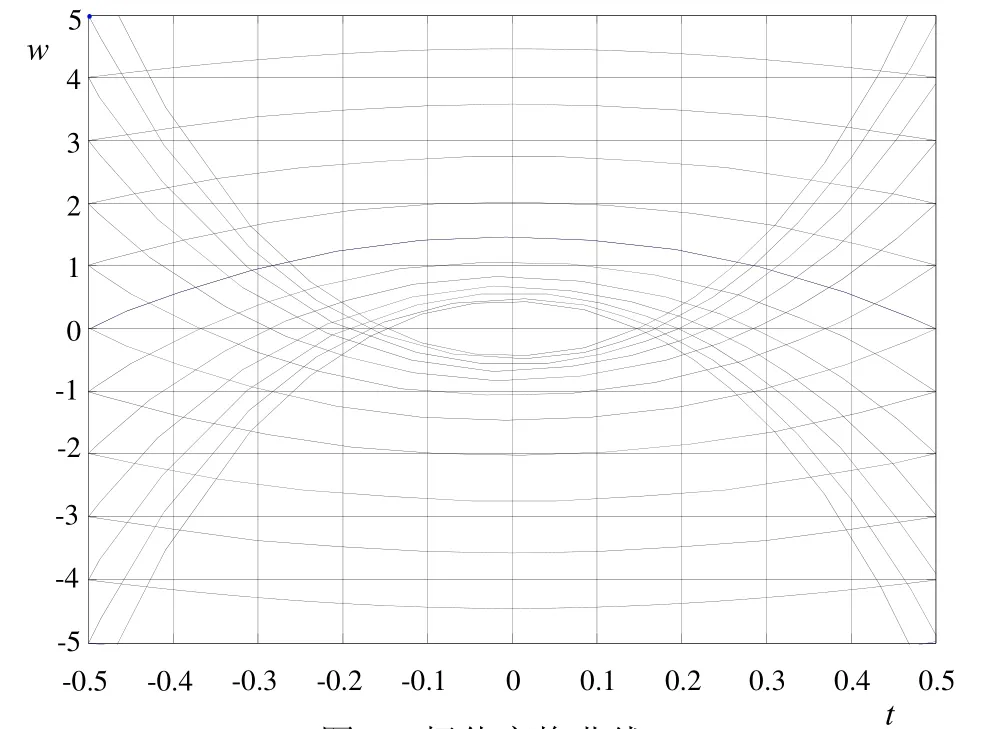
图7 极值变换曲线

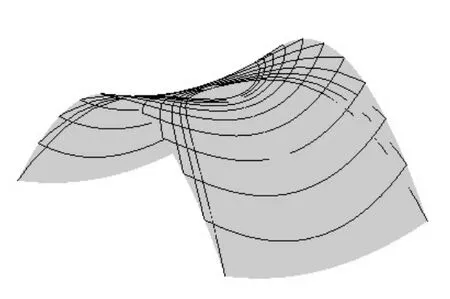
图8 双曲抛物面上的极值变换曲线

6） 等距变换曲线

由式（10）有

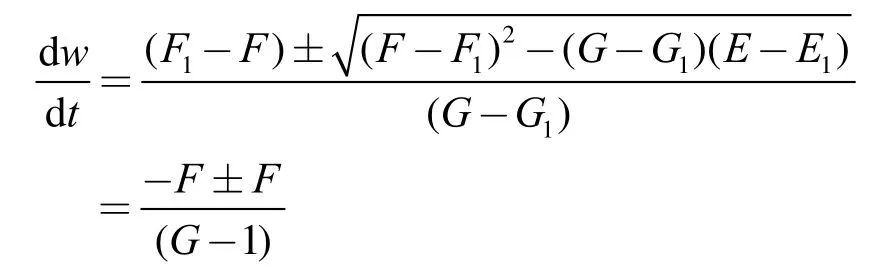
解此微分方程可得另一族等距变换曲线。图9是过点 t= 0.5，w =− 5,− 4.75,− 4.5…诸点的等距变换曲线，图 10为其在双曲抛物面上的映射结果。

7） 综合分析

在双曲抛物面与其可展切柱面的映射中，因t曲线长度没有变化，所以两曲面在t参数方向上有着很好的接近程度；而在w参数方向上，随着参数的增大，w曲线的长度以近平方速度迅速增大，这也导致对应区域面积变化以相同趋势迅速增大和两曲面的迅速离开；参数曲线交角变化随着两参数的增加约呈线性趋势增加。过曲面上任意对应点，随着切方向变化，长度比分别两次取极值和零值，对应着过该点的两条极值和两条等距变换曲线。在双曲抛物面近似展开和平面与双曲抛物面的纹理映射时，t参数方向可取较大范围，而w参数方向上应取较小范围以控制误差；纹理中主要几何要素若取在等距变换曲线上，能有效控制映射中的变形。

图9 等距变换曲线

图10 双曲抛物面上的等距变换曲线

4 结 束 语

本文提出了构造曲面片的可展切曲面及它们间映射分析的方法，并给出了应用举例。曲面片的可展切曲面可以应用于曲面结构设计、不可展曲面的近似展开、平面与曲面间的纹理映射等场合，有利于提高曲面成形及曲面映射的精度；曲面片与其可展切曲面间的映射分析便于较准确地把握曲面的变形情况，可用于曲面近似展开的精度分析与误差校正、纹理映射时的变形控制等场合。

[1] Aumann G. A simple algorithm for designing developable Bezier surfaces [J]. Computer Aided Geometric Design, 2003, 20(8-9): 601-619.

[2] 王树勋, 叶正麟. 可展 Bézier曲面的设计[J]. 计算机工程与应用, 2007, 43(23): 21-23.

[3] 陈志飚, 赵 耀, 严 俊. 船体曲面柔性敷设块的展开[J]. 工程图学学报, 2006, 27(1): 119-123.

[4] 杨继新, 刘 建, 肖正扬, 等. 复杂曲面的可展化及其展开方法[J]. 机械科学与技术, 2001, 20(4): 520-521.

[5] 李 亮, 邓建松. 近似可展曲面的构造及应用[J].高等学校计算数学学报, 2006, 28(4): 374-384.

[6] 孟雅琴. 可展曲面的构造与插值研究[M]. 上海: 上海交通大学出版社, 2010: 3-25.

[7] 毛 昕, 侯 悦. 不可展回转曲面近似展开的精度分析[J]. 工程图学学报, 1998, 19(3): 1-10.

[8] 毛 昕, 侯 悦. 回转曲面近似展开的数学模型[J].工程图学学报, 1999, 20(4): 1-6.

[9] 丁 森. 不可展曲面近似展开中若干问题的研究[D].沈阳: 东北大学, 2011.

[10] 梅向明, 黄敬之. 微分几何[M]. 北京: 人民教育出版社, 1981: 87-110.

The developable tangent curved surface of a surface patch and mapping analysis between them

Mao Xin, Yang Jinglin, Ma Mingxu
( Mechanical Engineering and Automation School, Northeast University, Shenyang Liaoning 110004, China )

Based on the developable curved surface theory of differential geometry, the method to construct the developable tangent curved surface passed a curve on a curved surface is put forward, the expression form and type division of the developable tangent curved surface is given, the overall and partial mapping analysis between two surfaces is realized through establishing the mapping relationship of them and the deformation of surface is grasped accurately. The method is validated by example and can be applied to the design and approximate development of curved surface and surface texture mapping.

geometry calculation; developable tangent curved surface; mapping between surfaces; deformation analysis

TB 21

A

2095-302X (2012)06-0031-07

2011-04-17；定稿日期：2011-06-07

毛 昕（1954-），男，吉林长春人，教授，硕士，主要研究方向为计算机图形学及辅助设计、理论与应用图学。E-mail：ddmx54@sina.com