堰塞坝漫顶溃决过程数值模拟
2012-04-17钟启明陈生水赵联桢
钟启明,陈生水,赵联桢,任 强,曹 伟
(1.南京水利科学研究院岩土工程研究所,江苏南京 210029;
2.南京水利科学研究院水文水资源与水利工程国家重点实验室,江苏南京 210029;
3.南京林业大学土木工程学院,江苏南京 210037)
地震、降雨等自然灾害往往引发大规模滑坡和山体崩塌,使受灾区域河流阻塞,形成天然堰塞坝。堰塞坝的工作条件、坝体几何特征以及坝体物质组成和内部结构都与人工土石坝存在明显差别。首先在工作条件上,因没有溢洪道和其他泄洪设施,上游持续来水使坝前水位快速上涨,堰塞坝很容易发生漫顶溃决;其次从坝体形态来看,堰塞坝坝顶一般凹凸不平,存在天然凹槽,且体型多呈不规则形状,沿河流方向堆积范围明显超过狭窄河谷的宽度;再者从坝体结构来讲,因坝体材料没有经过人工筛选和施工碾压,大部分堰塞坝结构疏松,不均匀性强,坝体材料多为砾石、粗颗粒,粗细混杂,粒径级配范围变化大[1-2]。调查表明[3],90%的堰塞坝都在其形成1a内溃决。一旦发生溃决,所产生的洪水或泥石流将对下游产生严重危害。因此,有必要研究堰塞坝漫顶溃决机理及溃决过程,为正确评估堰塞坝溃决致灾后果、科学制定堰塞坝溃决防洪应急预案提供技术支撑。
1 堰塞坝溃决机理和溃决过程分析
目前关于堰塞坝溃决机理和溃决过程的研究工作主要参考人工土石坝的成果,对于如何合理模拟宽级配堰塞坝材料在高强度水流侵蚀条件下的非平衡冲刷特性的研究工作很少涉及。王光谦等[4]提出在堰塞坝溃坝模型中考虑溃口水力冲刷和重力坍塌扩展,但是该模型使用的冲蚀公式是在恒定均匀流条件下建立的一般平衡冲蚀公式;黄金池[5]利用水槽试验结果,将高强度水流非平衡冲刷公式引入到溃口扩展模型,并将溃口垂直下切、横向扩展、坝坡溯源冲刷3种过程结合起来建立堰塞坝溃坝数学模型,但是该模型的冲蚀公式主要基于室内平面水槽试验,泥沙粒径范围为0.18~13.00mm,无法合理反映堰塞坝边坡上砾石、块石等大粒径滑坡堆积物的起动问题,且冲蚀公式中的参数不易获取。
要正确模拟堰塞坝漫顶溃决过程,需要从堰塞坝材料粒径范围宽的特点入手,同时考虑坝体密实度、坝体材料强度、下游坡度、漫顶水流流速的影响。笔者基于上述考虑,根据堰塞坝坝体材料的宽级配特性,建立描述堰塞坝漫顶溃决溃口发展规律与流量过程的数值模型,并利用该模型对唐家山堰塞坝的溃决过程进行数值模拟,验证了该模型和计算方法的合理性。
2 堰塞坝漫顶溃决过程数值模型
2.1 宽级配坝体颗粒临界起动流速
堰塞坝漫顶溃决过程中水流的冲蚀过程以及非均匀岩土颗粒的起动具有非恒定的特性。假设水流作用下忽略颗粒间的黏性特征,首先根据堰塞坝坝体土石料颗粒的受力情况求得颗粒起动的临界流速(图1)。
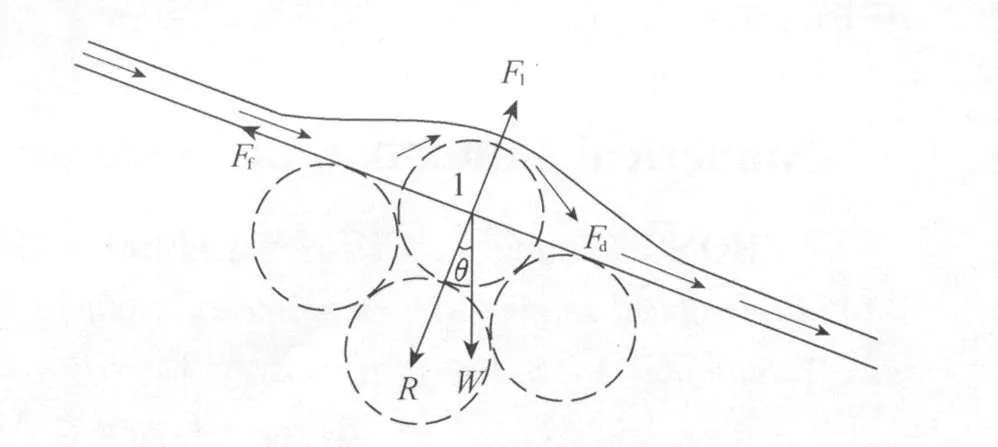
图1 土体颗粒在坝坡上的受力示意图Fig.1 Forces acting on a soil particle along dam slope
对土体代表颗粒1而言,考虑水流作用下岩土体颗粒所受的力一般有重力W、水流拖曳力Fd[6]、上举力Fl[6],其表达式分别为

式中:ρs——土颗粒的密度;ρw——水的密度;d50——土颗粒的平均粒径;g——重力加速度;Cd——拖曳力系数,一般取0.4[7];v——水流流速;Cl——上举力系数,一般取0.1[7]。
需要指出的是,堰塞坝体土石料级配宽泛,最大粒径和最小粒径相差很大。为此,引入与水流方向垂直的附加作用力R(图1)来考虑粗颗粒对细颗粒的阻拦、遮蔽作用以及细颗粒对粗颗粒的包围、填实作用。由于目前对R的研究很少,尚无精确理论公式,可近似假定R与颗粒的平均剪力成比例[8-11],即

其中
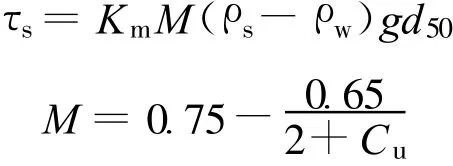
式中:R——附加作用力;φ——比例系数与颗粒面积系数的乘积;τs——不均匀颗粒的平均剪力;Km——无因次系数;M——紧密系数,代表颗粒组成的密实程度,反映颗粒组成的不均匀程度和细颗粒填充孔隙的程度[9];Cu——不均匀系数。
由式(4)可得

其中

式中K为系数,可以根据不均匀颗粒起动流速试验资料及天然河流实测资料确定,在0.785~1.727范围内变化,此处取1.3[9]。
如图1所示,土颗粒起动时受到的摩擦力可表示为

式中:Ff——土颗粒受到的摩擦力;φ——土颗粒间的内摩擦角;θ——坝坡坡角;c——土体的黏聚力。通过受力分析可知,土颗粒1起动的临界条件为

将式(1)(2)(3)(5)(6)代入式(7)可得土颗粒在坝坡上的临界起动流速:

2.2 临界起动流速公式验证
唐家山堰塞坝溃决过程中,现场测量得到坝体颗粒的起动流速为2.4m/s[12],因此,可利用该起动流速来验证本文提出的临界起动流速公式的合理性。根据相关资料[13],计算参数取值为:d50=0.03m,c=60kPa,M=0.75,θ=23°,φ=45°,g=9.8m/s2,ρs=2.6×103kg/m3。将上述参数代入式(8),可计算得出临界起动流速vc=2.12m/s(如不考虑附加力作用,临界起动流速为1.35m/s),与实测结果基本一致,验证了宽级配颗粒起动流速的合理性。
2.3 坝顶溢流冲刷速率
当土体颗粒在水流作用下起动后,在溃坝水流的作用下,坝顶溃口和下游坝坡发生冲蚀,由于坝体材料粒径级配范围变化大,因此在分析不同土体陡水槽冲蚀试验结果[14-16]的基础上,选择d90与d30为代表粒径,笔者建议了一个计算堰塞坝土石料冲蚀率的经验公式:
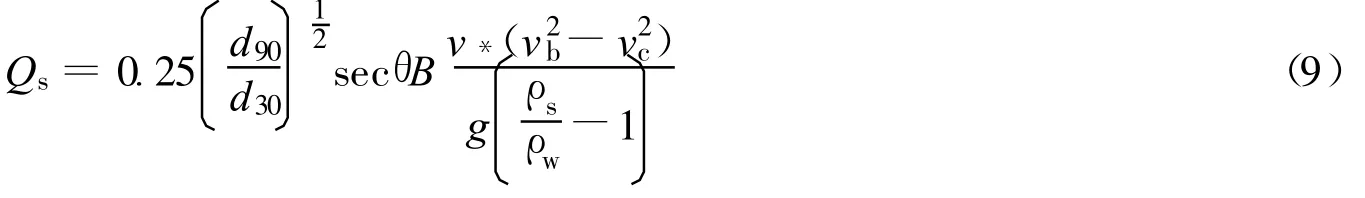
其中
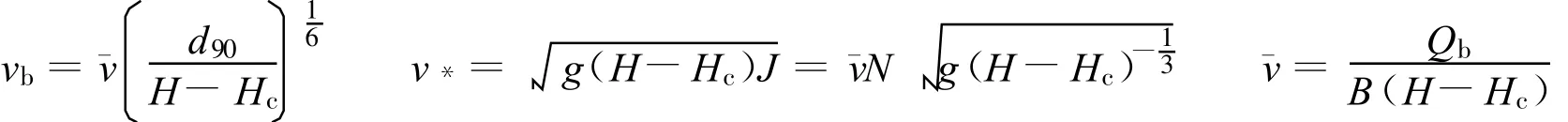
式中:Qs——水流冲蚀率;d90——小于某粒径土石料质量分数为90%所对应的颗粒粒径;d30——小于某粒径土石料质量分数为30%所对应的颗粒粒径;B——溃口宽度;v*——摩阻流速;vb——溃口底流速;¯v——水流平均流速;H——堰塞湖水位高程;Hc——溃口底部高程;J——水力梯度;N——溃口处糙率;Qb——溃口流量。
当漫顶溃坝发生后,水流沿着初始溃口冲蚀下游坝坡,溃口流量可采用以下宽顶堰公式计算:

式中m为流量系数,此处可取0.5[17]。
2.4 冲蚀公式验证
建议的坝体材料冲蚀公式可反映筑坝材料颗粒级配、密实度、强度、渗透通道倾角和坝坡、摩阻流速及水流速度对冲蚀量的影响,公式中各物理量意义明确且易于测定。为了验证所建议公式的合理性,运用该公式对4种不同土体的单宽冲蚀量进行计算分析,计算结果与陡水槽冲蚀试验结果[14-16]的对比见图2。从图2可以看出,计算结果位于试验结果的变化区域内,这表明从工程应用角度来看,所建议的坝体材料冲蚀公式是可以接受的。

图2 水流流速与单宽冲蚀率的关系Fig.2 Relationship between flow velocity and erosion rate
2.5 溃口发展
土石坝漫顶破坏溃口发展状况见图3。坝体初始溃口形状并非一直保持不变,而是随漫顶水流流速的增大和坝体冲蚀的加剧不断加深加宽,时间段增量Δti内水流下切深度增量为

时间段Δt内水流下切深度增量为

式中j为Δt时段内的时间步长数。
如果不考虑溃口边坡失稳和坍塌引起的溃口横向扩展,溃口底部的冲蚀速率应和溃口边坡的冲蚀速率大体相等,因此假定溃口的深度和宽度以同样的速率发展[18],则水流对坝体溃口两侧的直接冲刷形成的溃口宽度增量ΔB可表达为

时间段Δt内水库水位变化量为

式中:Qin——入库流量;Sa——库水位为H时的水库面积。
溃口受到水流的连续冲蚀发生垂向下切和横向扩展,边坡也随水流冲蚀变得越来越陡,当垂向下切深度达到临界深度时,溃口边坡发生间歇性失稳坍塌(图3)。临界深度可采用极限平衡方法导出[18]:
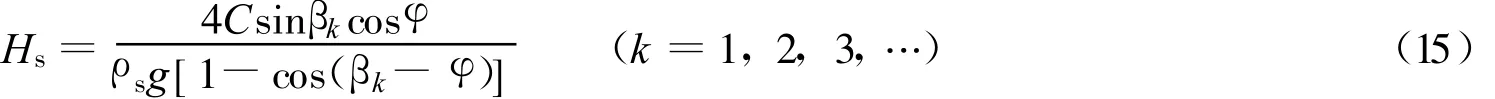
式中βk为溃口边坡临界坡角。
3 数值计算方法
可通过迭代计算来对上述溃坝数学模型进行求解,以模拟堰塞坝漫顶破坏溃口发展过程,得出溃口流量过程线。为证明所建议模型的有效性和合理性,针对堰塞坝漫顶引起的溃坝问题,进行溃坝洪水过程计算,计算实例为唐家山堰塞坝,具体求解过程见图4,图中Hbm为溃口最终底高程,Bu为溃口最终顶宽,Bm为溃口最终底宽。

图3 土石坝漫顶破坏溃口发展示意图Fig.3 Breach development of earth-rocKdam due to overtopping failure
4 模型验证
“5.12”汶川大地震堵江形成的堰塞坝中以唐家山堰塞坝规模最大,对下游威胁也最大。坝体位于北川县城上游4.6km涪江支流通口河峡谷中,其堰塞坝体积约为2037万m3,按我国堰塞湖坝体等级划分,唐家山堰塞坝属于极高危险、溃决损失极严重的Ⅰ级风险堰塞坝[19]。
堰塞体的基本形状为宽顶堰,上游坡度18°~22°,下游坡度35°~40°。顺河向堰顶宽度为150m左右,堰塞体除表部少量为碎石土外,主体为基岩滑坡形成的巨石、孤块石,其中下部岩性为弱风化~微风化,仍保持原地层层序关系,破裂岩体结构密实,强度高。坝体最大坝高124.4m,顺河向底长803.4m,顶长300.0m左右,宽611.8m,体积约为2.037×107m3,坝底高程为669.5 m,上游坡度约为20°,下游平均坡比为1∶1.28[19]。经过应急抢险,截至2008年6月1日,堰塞坝顶开挖出1条梯形泄流槽,断面形状为梯形,两侧边坡为1∶1.5。泄流渠堰顶高程为740.4m,底宽8 m,深13m,总长695m,上游平缓段纵坡为0.6%,下游陡坡段纵坡分别为24%和16%[19]。
由于泄流槽经2次爆破,6月10日才开始泄流,所以选取6月10日0:00为起始计算时间。根据上述基本条件,计算时间步长取Δt=0.02h,计算时间设定为20 h。其他计算参数如下:堰塞体高度为124.4m,堰塞体横河向顶宽为611.8m,堰塞体顺河向长度为300.0m,下游平均坡比为1∶1.28,初始溃口宽度为8.0m,初始溃口深度为13m,上游入库流量为0m3/s,堰塞体平均粒径为0.03m,粒径比d90/d30为30,堰塞体孔隙率为0.4,堰塞体材料平均密度为2.6×103kg/m3,内摩擦角为45°,堰塞体下游平均坡角为23°,堰塞体黏聚力为60kPa,紧密系数为0.75,流量系数为0.5。
计算得出唐家山堰塞坝溃坝洪峰流量出现在坝体溃决后11.8h,洪峰流量为6137.4m3/s(实测最大值为6500.0m3/s[19]),见图5。图6为溃口发展过程,溃口顶宽202.0m,底宽120.7 m,深度22.0m(实测溃口呈上宽下窄的“倒梯形”,其开口宽145.0~225.0m,底宽100.0~145.0m,坡高10.0~60.0m[19])。由图5~6可知,计算结果与实测资料接近,表明笔者所建议的堰塞坝溃坝数值模型和数值计算方法是合理的。

图4 堰塞坝漫顶溃决数值模拟流程Fig.4 Flow chart of numerical simulation of barrier dam breach due to overtopping failure

图5 溃口流量过程对比Fig.5 Comparison of calculated and observed discharge hydrographs at breach
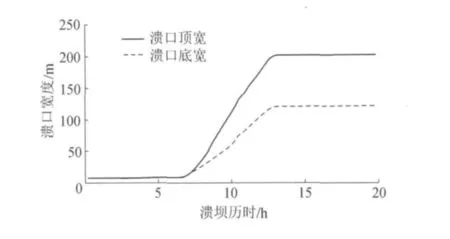
图6 溃口发展过程Fig.6 Breach development
5 结 语
根据堰塞坝坝体土石料的宽级配特性,建立描述堰塞坝漫顶溃决过程中溃口发展规律与流量过程的数值模型。该模型引入与水流方向垂直的附加作用力来考虑粗颗粒对细颗粒的阻拦、遮蔽作用以及细颗粒对粗颗粒的包围、填实作用。基于不同土体陡水槽冲蚀试验结果,针对宽级配堰塞坝材料在高强度水流侵蚀条件下的冲蚀特性,提出了一个能反映坝体材料颗粒级配、密实度、强度、坝体坡度、水流速度及摩阻流速对冲蚀量影响的土体冲蚀公式,公式中各物理量意义明确且易于测定。利用该模型对唐家山堰塞坝的溃坝过程进行模拟计算,得出的溃口发展规律与溃坝洪水流量过程与实测结果接近,验证了该模型和计算方法的合理性,从而为正确评估堰塞坝溃决致灾后果、科学制定堰塞坝溃决防洪应急预案、减轻因堰塞坝溃决造成的损失提供了一种新的有效手段。
[1]任强,陈生水,钟启明,等.堰塞坝的形成机理与溃决风险[J].水利水电科技进展,2011,31(5):30-34.(REN Qiang,CHEN Shengshui,ZHONG Qiming,et al.Formation mechanism and breaching failure risKof barrier dams[J].Advances in Science and Technology of Water Resources,2011,31(5):30-34.(in Chinese))
[2]邓明枫,陈宁生,胡桂胜,等.松散及弱固结堰塞体溃坝形式与流量过程[J].水利水电科技进展,2011,31(1):11-14.(DENGMingfeng,CHEN Ningsheng,HUGuisheng,et al.Outburst patterns and discharge process for weakly consolidated and loose barrier dams[J].Advances in Science and Technology of Water Resources,2011,31(1):11-14.(in Chinese))
[3]COATA JE,SCHUSTER RL.The formation and failure of natural dams[J].Geological Society of America Bulletin,1988,100(1):1054-1068.
[4]王光谦,钟德钰,张红武,等.汶川地震唐家山堰塞湖泄流过程的数值模拟[J].科学通报,2008,53(24):3127-3133.(WANG Guangqian,ZHONG Deyu,ZHANGHongwu,et al.Numerical simulation of dischargeprocess for Tangjiashanbarrier lake due to Wenchuan earthquake[J].Chinese Science Bulletin,2008,53(24):3127-3133.(in Chinese))
[5]黄金池.堰塞坝漫顶溃口流量变化过程的数值模拟[J].水利学报,2008,39(10):1235-1240.(HUANG Jinchi.Numerical modeling of flow through breach of landslide dams[J].Journal of Hydraulic Engineering,2008,39(10):1235-1240.(in Chinese))
[6]钱宁,万兆惠.泥沙运动力学[M].北京:科学出版社,2003.
[7]韩其为,何明民.泥沙起动规律及起动流速[M].北京:科学出版社,1999.
[8]李荣,王迎春.非均匀沙起动规律研究[J].泥沙研究,1999(2):27-32.(LI Rong,WANG Yingchun.Study on laws of threshold motion for non-uniform sediment[J].Journal of Sediment Research,1999(2):27-32.(in Chinese))
[9]秦荣昱,王崇浩.河流推移质运动理论及应用[M].北京:中国铁道出版社,1996.
[10]王协康,敖汝庄.泥沙起动条件及机理的非线性研究[J].长江科学院院报,1999,16(4):39-41.(WANG Xiekang,AO Ruzhuang.Nonlinear study on sediment incipient motion condition and its mechanism[J].Journal of Yangtze River Scientific Research Institute,1999,16(4):39-41.(in Chinese))
[11]杨具瑞,方铎,何文社,等.非均匀沙起动规律研究[J].水利学报,2002,33(10):82-86.(YANG Jurui,FANG Duo,HE Wenshe,et al.Study on laws of incipientmotionfor non-uniform sediment[J].Journal of Hydraulic Engineering,2002,33(10):82-86.(in Chinese))
[12]LIU Ning,CHEN Zuyu,ZHANG Jianxin,et al.Draining the Tangjiashan barrier lake[J].Journal of Hydraulic Engineering,ASCE,2010,136(11):914-923.
[13]胡卸文,黄润秋,施裕兵,等.唐家山滑坡堵江机制及堰塞坝溃坝模式分析[J].岩石力学与工程学报,2009,28(1):181-189.(HUXiewen,HUANG Runqiu,SHI Yubing,et al.Analysis of blocking river mechanism of Tangjiashan landslide an dambreaking mode of its barrier dam[J].Chinese Journal of RocKMechanics and Engineering,2009,28(1):181-189.(in Chinese))
[14]MEYER-PETER E,MULLER R.Formulas for bed load transport[C]//Proceedings of Second Meeting International Association for Hydraulic Research.Stockholm:IAHR,1948:39-64.
[15]SMARTG M.Sediment transport formula for steep channels[J].Journal of Hydraulic Engineering,ASCE,1984,110(3):267-276.
[16]范家骅,陈裕泰,金德春,等.悬移质挟沙能力水槽试验研究[J].水利水运工程学报,2011(1):1-16.(FAN Jiahua,CHEN Yutai,JIN Dechun,et al.Experimental studies on carrying capacity of suspended load[J].Hydro-Science and Engineering,2011(1):1-16.(in Chinese))
[17]李家星,赵振兴.水力学[M].南京:河海大学出版社,2001.
[18]SINGH V P.Dam breach modeling technology[M].Dordrecht,Netherland:Kluwer Academic Publisher,1996.
[19]刘宁,张建新,林伟,等.汶川地震唐家山堰塞引流除险工程及溃坝洪水演进过程[J].中国科学E辑:技术科学,2009,39(8):1359-1366.(LIU Ning,ZHANG Jianxin,LIN Wei,et al.Drainage reinforcement project and dam breaKflood process of Tangjiashanbarrier due to Wenchuan earthquake[J].Science in China E:Technological Sciences,2009,39(8):1359-1366.(in Chinese))
