阀体后90°圆形弯管内部流场PIV测量及POD分析

谢 龙，靳思宇，2，王玉璋，于建国

（1.上海交通大学动力机械与工程教育部重点试验室，上海 200240；2.中国船舶重工集团公司第704研究所，上海 200031）

0 引 言

弯管流动受到诸多因素的影响，尤其是在弯管前端存在阀门时，弯管内的流场呈现出十分复杂的流动特性，如在管内壁附近形成二次流动分离区、管外侧产生大尺度涡街，这些现象不利于流体输运的平稳性能，造成流体总压和能量的损失，并且特殊的流动结构还对管道噪声特性有着重要影响。

弯管流动的研究一直受到内流研究者的关注［1－7］。文献［2－3］中分别采用基于重整化群方法提出的RNG k－ε湍流模型和大涡模拟（Large Eddy Simulation，LES）对弯管内部流场进行数值模拟，揭示了管道横截面上的二次流动及沿流向的压力分布。文献［4－6］中分别采用旋转探针技术、激光多普勒测速仪、CTA热线风速仪和五孔探针对不同曲率直径比Rc／D（Rc、D分别代表曲率平均半径和弯管的水动力直径）的圆形或方形截面弯管内部流场进行了试验研究。已有文献的研究主要关注无阀门、大曲率直径比90°弯管的流动特性，对弯管前段存在阀门，或Rc／D＜1.0的圆截面弯管流动，无论试验还是理论研究都进行得比较少，而这类弯管在工业中应用却十分广泛，因此，已有研究对工程应用贡献有限。

针对这种情况，结合某工程实际问题，对前端配置蝶阀，Rc／D＝0.75、D＝200mm的90°圆截面弯管内部流场进行了PIV测量及POD分析。研究结果对进一步揭示阀体后弯管内流动特性具有重要参考价值；为以后继续研究管道噪声与流场涡结构特性等之间的关系打下了基础，对于弯管降噪的研究具有重要意义。

1 试验设备

试验装置主要包括管路系统、试验段和PIV测量系统［7］。管路系统为试验搭建的低速循环水槽。试验工质水由磁力泵驱动，通过变频仪调节水泵转速，以达到对试验段流速的控制。循环水从水箱引流，由磁力泵驱动并经过整流进入试验测量段，通过试验段后，用电磁流量计测量流速，控制流量为226.08～452.16m3／h，对应于来流速度为2～4m／s。本次试验工质水含有大量粒子，试验前经测试，粒子具有良好的跟随性、光散射性且分布均匀，满足示踪要求，故试验中不需要额外添加示踪粒子。

试验段结构如图1所示。其中，Rc／D＝0.75，D＝200mm。在试验段前端，安装控制开度的一次偏心蝶阀（其阀杆轴心偏离了蝶板中心，从而使得蝶板上下端不再成为回转轴心），蝶阀偏心距30mm，阀杆轴心与弯管入口平面距离L＝112mm，试验中蝶阀保持全开的开度。均匀来流在蝶阀以及弯管的约束作用下产生复杂流动，试验测量区取在流速变化剧烈的弯管段，如图1中阴影部分所示。以蝶阀所处位置为参考将测量区分为外侧区域和内侧区，取区域间的交界线（虚线）为特征线。试验段有机玻璃窗口处于弯管上部以及外侧面，分别用于拍摄与激光照明。图2为试验测量区域截面示意图，试验测量段的拍摄截面以管中心为基准面，选取在z向彼此相距10mm的9个水平测试截面。

高分辨率PIV测量系统基于Dantec Dynamics公司的二维粒子图像测速系统构建。主要组成为：双谐振脉冲式Nd：YAG激光器、高分辨率工业相机FlowSense 4MMKII（分辨率为2048pixel×2048pixel）、同步时序控制器Timer Box 80N75及PIV应用软件。其中，激光器片光源镜头及相机通过二维坐标架实现纵向位移的精确控制，相机工作频率7.4Hz，跨帧延时100μs，所拍摄试验段图像与实际尺寸之间的转换通过拍摄标尺图像进行图像标定来完成。互相关图像分析采用先进的多重网格迭代计算、多重自适应变形窗口算法、判读区交叠查询及互相关峰值确定的高斯拟合方法，计算结果可达±0.1pixel的亚像素精度［8］，并对处理出的矢量场进行进一步的相干性过滤及局部有效性判定，所分析出的速度场真实反映了高分辨率流动瞬态图像所记录的实际流动信息。

图1 试验段弯管结构示意图Fig.1 Schematic diagram of the bend of measured section

图2 拍摄截面Fig.2 Shooting section

2 结果与分析

2.1 PIV测量结果

图3为阀体后弯管流场的瞬态速度矢量图及特征线上的速度分布。流动的典型特征为流体在弯管圆弧内壁的作用下顺时针转向与来流垂直的方向。因蝶阀对来流的有效阻滞作用面积较小，阀体后形成的分离区内速度与来流流速相差不大，从而不能造成强烈的剪切流动并形成弯管段内可以观测的较大尺度的涡旋结构。内侧壁面涡流的生成因为大尺度均匀来流的存在而受到抑制，因此图3（a）中弯管内侧速度矢量分布均匀；外侧矢量方向沿流向存在不规则摆动，且幅度逐渐变小直至最后出口段所有矢量互相平行，对比已有弯管研究结果［1］，可以推论外侧有小尺度的涡旋从蝶阀后的分离流中生成并脱落。利用瞬态速度场减去时均速度场得到脉动速度场，提取脉动速度场中蝶阀所处位置流线上的速度分布，如图3（b）所示，弯管外侧流体沿流向存在逐渐减弱的速度起伏波动，表明该特征线上存在沿流动方向逐渐减弱的涡列。

图4为时均速度矢量图及以速度云图为背景的流线图。弯管内侧为流动高速区［1］，原因是弯管段存在由外侧指向内侧的压力梯度，在此压力梯度作用下在垂直于流向的横截面上产生一组上下反对称的涡流二次流，且涡核位置随着流动的发展逐渐偏向弯管内侧，截面上下两侧近壁面流动由外侧指向内侧，中间部分由内侧指向外侧［2－3］，该二次流与弯管主流的矢量和形成了内侧高速区，且流向以小角度向弯管外侧偏离该处弯管同心圆的切线方向。弯管外侧矢量分布均匀，说明瞬态场中观察到的涡街的时均流动效果为0。可以得出结论，阀体后扰流在弯管外侧区域产生的涡流结构具有宏观不可测性，但阀体后扰流在向下游输运的过程中会引起当地速度脉动，而所有脉动信息中涡结构对流场贡献权重大于流动噪声，因此可以从速度脉动中提取旋涡结构的信息。

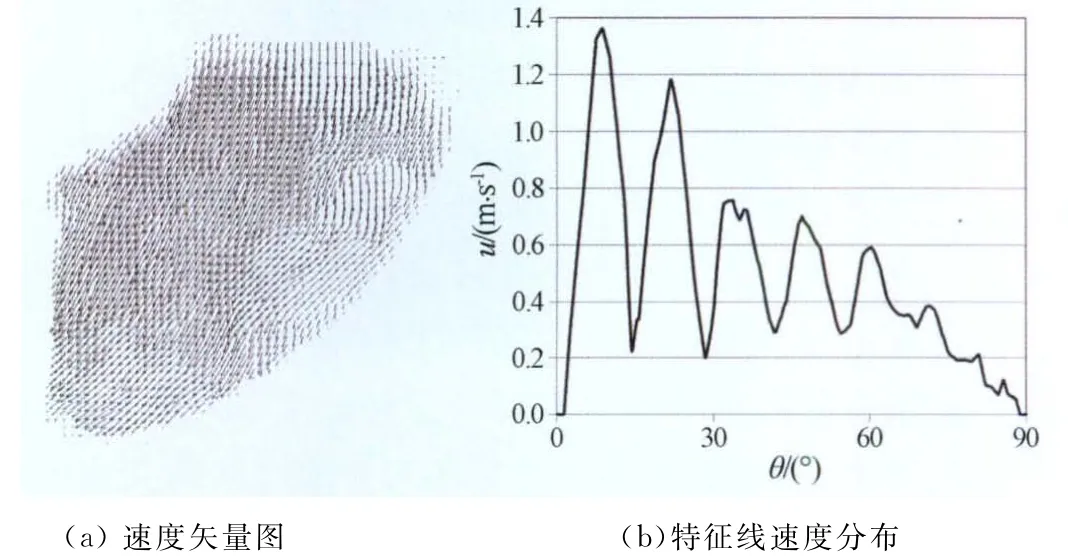
图3 瞬态流场Fig.3 Transient flow field

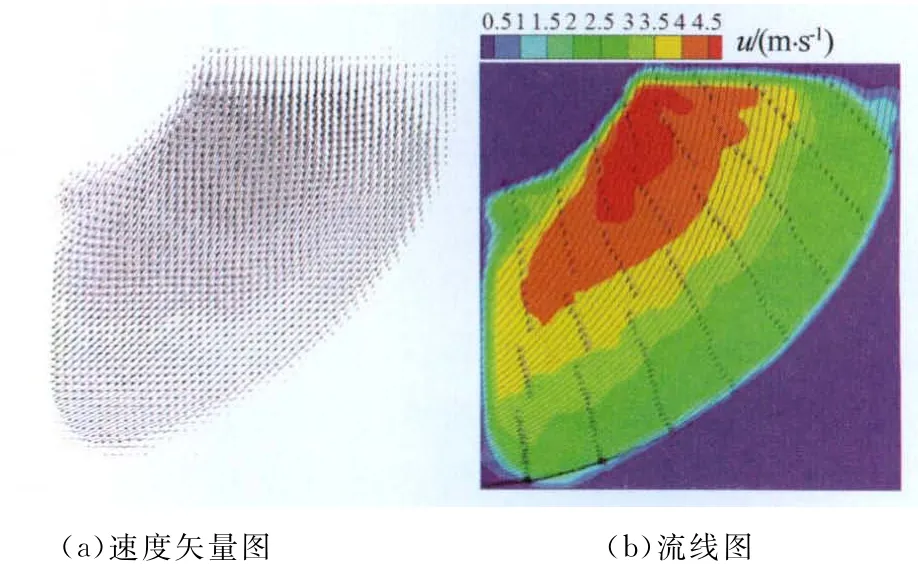
图4 时均流场Fig.4 Time－averaged flow field

2.2 流场POD分析

本征正交分解（POD）基于主元分析（PCA）思想，根据Karhunen－Loève展开将流场进行分解，按能量比计算出各阶模态，识别流动中的大尺度能级结构。POD之于PIV相当于LES之于CFD，POD对流动系统的识别旨在获得多维度系统的低维度近似描述，准确把握住主导的流动结构，对复杂流动进行合理的降阶研究。本征正交分解已经被广泛用于各种湍流速度场、涡量场、压力场等的研究中［9－11］。本次试验采用由Sirovich提出的快照POD法（snapshot POD）［12］，将速度场分解为时均速度场和脉动速度场，即u（x）＝ū＋u′（x），然后再对脉动速度场进行本征正交分解，全部流动信息便分解为时均流动（0阶模态）与脉动流动（分解为1，2，…阶模态）。给出0mm截面位置在3m／s来流速度工况下的POD分析结果。

图5为脉动速度场各模态能量分布（不包含0阶模态）。弯管速度脉动场的1阶模态占据了脉动动能的14.6%，在脉动流场中占据支配地位，适于用来描述典型的脉动；2～3阶模态的能量贡献次之，所占脉动动能比例分别为9.2%和6.8%，可认为这些模态对脉动流场起了重要作用。而后曲线的下降及后续的平整意味着高阶的模态对总动能的贡献很低，可以简单描述为流动噪声，如短暂的外部扰动、大尺度涡引起的高频小尺度结构或者耗散涡等。由于弯管中的涡街是脉动流的载体，因此脉动场的低阶模态中包含了弯管中的涡结构信息。

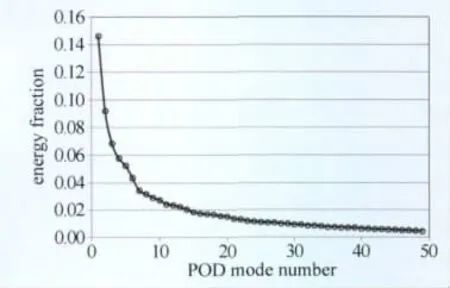
图5 POD模态能量分布Fig.5 POD modes energy distribution

1～3阶模态包含了阀体后扰流在弯管流场中产生的旋涡结构，除了简单的流线识别外，涡的识别方法有Calilean分解方法、LES分解方法、Reynolds分解方法、小涡分解方法、涡量方法和旋涡强度（swirling strength）方法［13］等。图6给出了1～4阶模态流动相干结构以涡量为背景的速度矢量图，其中表征时均流动的0阶模态前文已给出，图6中可见4阶模态已不具备明显的流动结构特征，再次说明4阶及其以上模态表征流动噪声。1～3阶模态中涡列中涡核间距离较为恒定，涡核出现位置近似处于蝶阀安装位置所在流线，且涡量数值分布为一正一负交替排列，说明沿流线旋涡旋转方向相反，这表现为典型的卡门涡街特征。过程为：在蝶阀前缘分离的剪切层，由于流体的粘性剪切作用使得剪切层卷起形成旋涡，而阀体两侧剪切层内涡对的相互吸引和相互作用，最终导致旋涡从阀体两侧剥离脱落，形成卡门涡街，以较高频率脱落的涡随流体进入弯管段，弯管横截面上的涡流二次流将卡门涡向外侧挤压，弯管外侧轮廓对涡流的向外侧发展产生束缚，同时旋涡本身从剪切层脱落以后相互吸引、相互作用，3种原因共同作用下使得旋涡的运动轨迹不断向阀体所在位置流线靠近，因此弯管中涡街的各个涡出现的位置近似在同一流线上；弯管横截面上二次流向外侧的偏移挤压及外侧壁面效应使涡外围能量随着流线逐渐削弱，同时随着卡门涡向下游的不断输运，涡的旋转与周围流体产生摩擦也耗散了部分涡能量，因此可清晰观测到涡量沿流线逐渐减弱的过程。根据涡量的定义ω＝▽×u，涡量方法除了识别出流场中的涡核，同时也反映了弯管流场中大量剪切运动信息。除脉动场中的涡结构以外，模态1中可以观测到由弯管内侧指向外侧的二次流动［2－3］；模态2中在弯管出口段还观测到大尺度不规则回流区，该回流由出口管外壁对出口斜射流的反作用逆压梯度引起；在弯管内壁出口位置也存在小尺度的涡流，这是由于内壁出口位置的局部低速区压力较高，与高速区形成的低压之间存在压力梯度，从而引起局部回流；流场中涡流区与二次流区以外为大范围的低速区。

图6 低阶POD模态相干结构Fig.6 Coherent structures of low POD modes

将流动状态投影到各POD模态，可以用若干基模态的线性组合来表示流场，即POD模态重构，模态重构可以还原主要流动结构。模态在重构具体流场时所承担的主要意义所占的比重由其对应的POD系数表征，图7给出了所研究时间范围内模态1的POD系数的时变图。POD系数随时间以类似正弦曲线的方式正负交替波动代表了该模态对应的流动结构随时间以正反作用交替的方式影响流动特性。由于该模态代表的是涡结构，因此其在流场中的作用体现为涡结构的顺时针与逆时针旋向交替。这是由于卡门涡街中涡旋总是以成对的旋转方向相反的反对称涡形式交错排列，流场中的固定空间点随时间受到不同旋向涡的作用。本次试验采用的高分辨率相机没有很好的时间分辨特性，只采样到流场中涡流旋向真实交替过程的几个片段，因此观测到的旋向交替过程中表现为正负值之间的大幅度波动，故试验不能反映实际流动中涡流旋向的交替频率，即卡门涡街脱落频率，但可以预计涡流旋向交替随时间的变化形态表现为一个周期很短的正弦函数［10］，且该频率远大于试验观测到的频率。

图7 模态1POD系数时变图Fig.7 Time－varying graph of POD coefficient value of mode 1

1～3阶模态中弯管外侧涡结构的能量逐渐减弱至很低的水平，4阶及以上模态已不具备明显流动结构特征，说明这3个模态中包含了阀体后弯管流场中由蝶阀扰流引起的大部分涡结构信息。排除时均流动与流动噪声，利用1～3阶模态重构流场可以还原弯管脉动场中由阀体后卡门涡引起的流动结构，得到无噪声情况下脉动流场的合理压缩。由于卡门涡以很高的频率从阀体后脱落，可以预计重构出的涡街中涡的旋向与强度随时间变化存在较大差异。针对还原的涡结构信息进行进一步分析可以揭示涡的流动特性，利用旋涡强度分布识别重构脉动场中的涡结构，用笛卡尔坐标下速度梯度张量的复特征值虚部分析能够使涡结构显示出来，并量化局部旋涡运动的强度，这一复特征值虚部定义为局部旋涡运动的旋涡强度。正特征值意味着流场中存在剪切流动，而不存在涡结构；负的旋涡强度表明该处有涡结构存在，而局部最小值则可以用来识别涡核的位置。图8给出弯管脉动流场信息POD重构出的典型涡街结构，其中计算结果只返回流场中的负特征值，而将正特征值全部设为0（红色区域），以排除剪切作用的影响。图中可以清晰观察到处于脱落过程中的卡门涡，涡列中相邻涡旋向交替、涡核位置近似处于同一流线、脱落过程中涡能量逐渐衰减。此外，“淹没”在下游主流中的旋涡也能从云图中观察到。

图8 旋涡强度分布Fig.8 Distribution of swirling strength

进一步的研究可以基于利用脉动主导模态重构的脉动场，对流场的降阶研究可以降低问题的复杂度，增强研究的针对性，且低阶模型具有较高精度。对固定来流流速、变观察截面的研究表明：由于阀体圆形结构在靠近上下端时尺寸逐渐变小，阀体对来流的有效阻滞作用减小，故相对于中间截面，上下两侧截面位置上阀体后涡流强度减小且其分离点更靠前，并以较小能量汇入主流，在弯管前的直管段内其能量已被大部分消耗，因此在弯管中仅有微弱的表现；在弯管横截面上涡流二次流的挤压下弯管中涡出现的位置在径向产生较大的指向外轮廓的偏移；同时观察到两侧截面上涡脱落频率小于中间截面，说明蝶阀后卡门涡街脱落频率与该截面上蝶阀长度正相关。对固定观察截面、变来流流速的研究表明：试验中阻流体迎面宽度恒定不变，卡门涡街脱落频率随来流流速成正比线性变化，因此在所研究流速范围以内，流场中的涡结构不随流速产生显著改变，随着流速的变化旋涡强度做近似线性变化。综上所述，弯管中的脉动大尺度结构为位于弯管外侧壁面附近的涡街，因此如果能改进该区域的脉动流，使该区域大尺度结构消除或弱化，将有利于流体输运的平稳性能在整体上的提高，进而有效降低流动噪声。改进方式包括调整蝶阀安装位置；将阀体背离来流部分补齐，使其表面接近流线型，从而消除旋涡的脱落；改进弯管外侧面结构或配合脉动缓冲器使用等。

3 结 论

（1）流体流经蝶阀在弯管中形成卡门涡街，涡流结构宏观不可测，可以从脉动速度场中提取旋涡结构信息；

（2）弯管中涡结构信息包含于低阶POD模态，低阶模态流动相干结构中涡列处于蝶阀安装位置所在流线，涡核间距恒定，相邻涡旋向相反，涡脱落过程中涡能量逐渐衰减；

（3）脉动场的模态重构可以准确还原弯管中的涡结构，弯管中间截面涡流强度大于上下两侧截面，蝶阀后卡门涡街脱落频率与该截面上蝶阀长度正相关，并随来流流速做近似线性变化。消除或减弱外侧壁面附近的大尺度涡结构将有利于流体输运平稳性能在整体上的提高，并降低流动噪声。

［1］ 江山，张京，伟吴崇，等.基于FLUENT的90°圆形弯管内部流场分析［J］.中国舰船研究，2008，3（1）：37－41.

［2］ 丁珏，翁培奋.90°弯管内流动的理论模型及流动特性的数值研究［J］.计算力学学报，2004，21（3）：314－321.

［3］ 梁开洪，曹树良，陈炎，等.入流角对圆截面90°弯管内高雷诺数流动的影响［J］.清华大学学报，2009，49（12）：1971－1975.

［4］ SUDO K，SUMIDA M，HIBARA H.Experimental investigation on turbulent flow in a circular－sectioned 90－degree bend［J］.Experiments in Fluids，1998，25（1）：42－49.

［5］ WILLIAMY，BENNY K.Experimental investigation of dilute turbulent particulate flow inside a curved 90°bend［J］.Chemical Engineering Science，2006，61（11）：3593－3601.

［6］ 尚虹，王尚锦，席光，等.90°圆截面弯管内三维紊流场试验研究［J］.航空动力学报，1994，9（3）：263－266.

［7］ 谢龙，靳思宇，于建国，等.阀体后90°圆形弯管内部流场PIV分析［J］.上海交通大学学报，2011，45（9）：1395－1399.

［8］ 万津津，施鎏鎏，余俊，等.贴壁方柱湍流场TR－PIV实验研究［J］.实验流体力学，2009，23（2）：31－35.

［9］ 阳祥，丁鹏，李增耀，等.基于POD方法的湍流大尺度信息提取与分析［J］.工程热物理学报，2010，31（6）：1019－1022.

［10］SHI Liu－liu，LIUI Ying－zheng，WAN Jin－jin.Influence of wall proximity on characteristics of wake behind a square cylinder：PIV measurements and POD analysis［J］.Experimental Thermal and Fluid Science，2010，34（1）：28－36.

［11］O'DONNELL B J，HELENBROOK B T.Proper orthogonal decomposition and incompressible flow：An application to particle modeling［J］.Computers and Fluids，2007，36（7）：1174－1186.

［12］SIROVICH L.Turbulence and the dynamics of coherent structures［J］.Quarterly of Applied Mathematics，1987，45（3）：561－590.

［13］ADRIAN M J，CHRISTENSEN K T，LIU Z C.Analysis and interpretation of instantaneous turbulent velocity fields［J］.Experiments in Fluids，2000，29（3）：275－290.