壁湍流调制雷诺应力和拟序结构应变率空间形态的层析PIV实验研究

贾永霞，姜 楠，2，3

（1.天津大学机械工程学院力学系，天津 300072；2.天津市现代工程力学重点实验室，天津 300072；3.中国科学院力学研究所非线性力学国家重点实验室，北京 100080）

0 引 言

壁湍流是粘性流体经过固体表面一定阶段后，由于流动不稳定性的作用，在固壁表面附近很薄的一层区域内发展成为平均流速沿壁面法向变化很快（梯度很大），而瞬时流动又极端混乱的流体流动状态。壁湍流可以使航空航天飞行器和船舶的表面摩阻大幅度增加，也会影响地球表面附近大气污染物的输运过程［1］。拟序结构对壁湍流的产生、维持和发展以及流体的质量、动量、能量的输运起着非常重要的作用。为了研究壁湍流中拟序结构动力学，将与流动有关的物理量分解为长时间平均量、拟序结构量和随机脉动量f′三部分［2］：

式中，bki（k＝1，2，…，Z；i＝1，2，…，5）表示k等级第i项主要因素的隶属度集中值，即加权平均值。

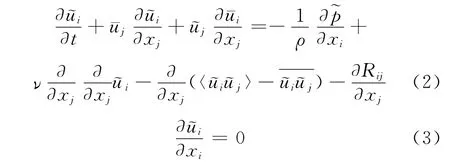
然而，在方程（2）中出现一项调制雷诺应力项，

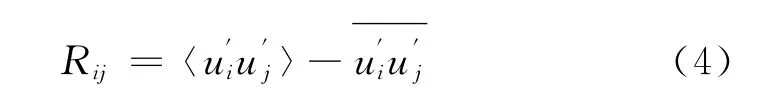
使得拟序结构动力学方程（2）不封闭。由于这一项是背景湍流雷诺应力的相位平均和长时间平均之差，Rij可以理解为拟序结构经过时背景雷诺应力的振动项，也称为调制雷诺应力。

应用空间流向局部平均速度结构函数的概念对湍流脉动速度信号进行分解，获得多空间尺度成分。为了分析一定空间尺度的湍流结构的流向拉伸、压缩变形，姜楠等［14］提出了局部平均结构函数的概念，描述长度为2a的一个湍流结构的流向拉伸或者压缩变形：

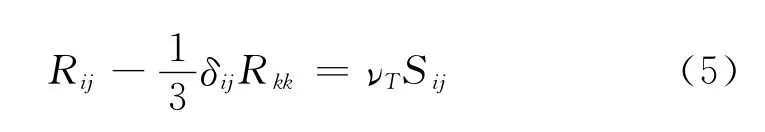
图6给出X－Z平面内拟序结构喷射过程中应变率分量与调制雷诺应力分量的空间相位平均分布等值面图，可以看出应变率6个分量的空间分布与对应的调制雷诺应力6个分量的空间分布的不一致性。调制雷诺应力分量R11，R33的空间分布几乎一致，都是在近壁区域达到极大值，而且在展向上呈现出准流向结构。拟序结构速度变形率分量S11，S22，S33的空间分布大概一致，在流向上呈现出周期交替性。切应力R12，R13，R23在流向上具有一定的准周期分布，应变率S12，S13，S23与各自对应的偏应力在空间分布上的相似性较差。

挂号窗口减少到5～6个，排队人数减少80%，整合岗位8个，分流员工10多人。门诊患者服务中心是一把钥匙，打开了医疗服务质量和效率提升之门。

通过仔细分析，笔者认为：无论虚压是通过哪一个用电设备“蹿”过来的，该用电设备一定会与12V常电相通，且一般情况下都会通过某个熔丝与12V常电相连。为此，笔者尝试着逐个拔下驾驶室内熔丝盒中的每一个熔丝，但拔下所有熔丝后，此电压仍旧存在。接着，笔者又开始检查发动机舱内熔丝盒中的熔丝，在拔下发动机舱内保险丝盒中的F12号熔丝后，此电压消失。查阅相关电路图发现，F12号熔丝负责给网关电脑供电。该车网关电脑J513装在油门踏板上方面的铁支架上。

对于壁湍流中第j尺度拟序结构的低速区喷射和高速区扫掠，可以通过流向局部平均速度结构函数过零点提取，这里下标e和s分别表示喷射和扫掠，D代表检测函数：

为了进一步研究包含相位信息的复涡粘模型，通过层析PIV获得了壁湍流三维测量体内瞬时速度场的时间序列，应用相位平均技术得到调制雷诺应力和拟序结构应变率的空间拓扑形态，研究了两者在拟序结构猝发过程中的空间分布，为进一步提出合理的非平衡湍流复涡粘张量模型提供了实验依据。

1 实验设备与技术

实验在自由来流速度为0.53m／s的水洞中进行。实验装置示意图见图1。平行于来流方向，垂直于底面插入一块有机玻璃光滑平板，固定于实验段的中心线处，平板长250cm，宽80cm，平板前缘为椭圆形，通过调节后缘襟翼保证零压力梯度。在平板观测面的前缘下游150mm处沿展向贴锯齿形条带，使得在测量点产生名义厚度38mm的湍流边界层，基于动量厚度的雷诺数为2460，自由来流湍流度低于0.5%。锯齿形条带距离壁面的高度为1.8mm，Elsinga and Westerweel［11］应用层析 PIV 做过研究，发现存在流动分离区，并在剪切层中发现波形状的展向涡，导致马蹄形涡和发卡涡的出现，他们得出结论，对于触发位置的湍流边界层厚度为δ0＝2.6mm，在大约下游500＊δ0的位置，这些过渡性的结构不再影响湍流边界中的流动结构。图2给出粘性内尺度单位无量纲化的对数律平均速度剖面，壁面摩擦速度通过u＋＝1／κ＊lny＋＋C在y＋＝40～200进行迭代，其中，κ＝0.41，C＝5.0，得到uτ＝0.0219m／s，壁面摩擦系数为uτ＝0.0035。这一结果与Schlatter等［12］的 DNS结果符合得很好。使用半导体泵浦双腔高频Nd：YLF激光器，脉冲能量为25mJ，脉冲频率为1kHz，以及6个1024pixel×1024pixel CMOS相机，构成了高时间分辨的层析PIV系统对壁湍流速度场进行测量，示踪粒子为直径56μm的聚酰胺微球。测量体的中心位于平板前缘下游2090mm处，以1kHz频率照明，测量体沿着x、y和z方向（x为流向，y为展向，z为壁面法向）大小约为63mm×68mm×15mm＝734pixel×793pixel×176pixel＝1380×1490×328壁面单位。以1kHz的频率拍摄5次，每次获得2040幅时间序列图像。系统使用DaVis7.3软件控制的LaVision Programmable Timing Unit（PTU9）进行同步控制。用PIV专用的MART层析方法［13］计算重构出三维粒子光强分布，得到了三维数字存储的光强体素阵列。用局部三维互相关和多重体变形网格迭代算法计算测量体内的速度场，互相关计算时的判读体大小为323体素，对应的空间分辨率为2.75mm×2.75mm×2.75mm，窗口重叠率为75%。最终获得92×99×22个空间测点的瞬时三维速度场分布的时间序列，其中时间序列步长为2ms。

公式（8）表示一个长度为2a的湍流结构的前后两部分的局部平均迁移速度差（局部平均相对速度），先分别在为中心，尺度为a的范围内对速度分量进行局部平均，得到这个湍流结构前后两部分的平均迁移速度，然后再求前后两部分的局部平均速度差（局部平均相对速度）。对于δu（aj，b）的极值点，表示长度为2a的一个湍流结构的流向拉伸或者压缩变形最为强烈的位置。对于δu（aj，b）的过零点，湍流结构的流向拉伸或者压缩最弱的位置，此部位的流体的迁移速度达到正的极大值或者负的极小值，代表拟序结构的低速流体区或者高速流体区。

图1 实验装置示意图Fig.1 Sketch of test section

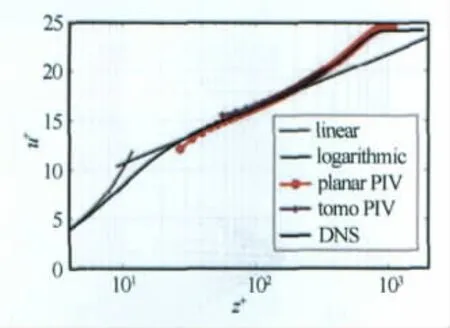
图2 雷诺数为2460的湍流边界层流向平均速度剖面Fig.2 Longitudinal mean velocity profile of TBL at Reθ＝2460

2 实验数据分析

Reynolds［2］提出准层流模型（Rij＝0），认为背景湍流应力对拟序结构的影响忽略不计，但是不能准确描述拟序结构在壁湍流中的运动行为。由于Rij是未知项，而且直到目前为止还没有通过实验获知它的物理机理，对它缺乏物理的认识，因此对于Rij的模拟，还只停留在借助于模型不变性的思想（Lumley［3］）和已有无扰动雷诺应力模型的认识的基础上。相干场的尺度和背景湍流场是不一致的。假设背景湍流演化需要的时间和空间尺度比拟序结构小得多，那么对于分子运动的牛顿粘性应力与流体微元应变的关系可能为调制雷诺应力模型提供基础。基于经典平衡态下Boussinesq假设，Poje［4］对调制雷诺应力引入一封闭模型：

水稻（Oryza sativa L.）不育系是杂交水稻研究与应用的重要技术载体。两系法杂交水稻具有育种程序和生产环节较简单、恢复谱广、配组自由度大等优点，因而选育优良两系不育系受到水稻育种家的广泛重视［1］。历经近40年的研究，全国已选育出一批光温敏核不育系如培矮64S、广占63S、Y58S、C815S、1892S等在生产上大面积应用［2］。本研究利用抗稻瘟病中籼光温敏核不育系E农1S为母本，以自育的两系不育系材料QFS－156作父本进行杂交选育，结合分子标记辅助选择和人工低温池加压选择，培育出不育起点温度较低、株型好、优质抗病、繁殖制种产量高的中籼光温敏核不育系EK2S。

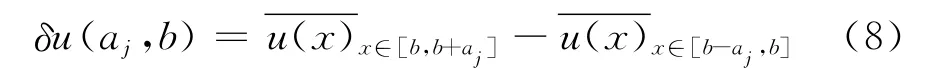
本研究写的是像藤尾那样的女性出现的背景，进一步与其他女性封建思想的女性对比。此外，在西洋文化的影响下，勇敢追求爱情的藤尾在利己主义和本位主义的驱使下，将难以舍弃私利的藤尾作为本论文的论点，研究像藤尾那样西化的女性的悲剧式人物。这是明治初期的西洋化女人的缩影，不仅是藤尾，还有很多像藤尾一样的女性也有着相似的命运。但是，西化的藤尾在与现实的斗争的研究资料也很少。

将涡粘性系数νT设成复数，相当于拟序结构的速度变形率与调制雷诺应力之间存在着相位差。在湍流中涡粘性产生的原因是不同宏观时空尺度拟序结构间的动量交换。与分子运动论类似，当具有宏观时空尺度的拟序结构进行迁移时，也会与其它的拟序结构发生相互作用，相互之间发生动量交换，即为雷诺应力的相互作用。但是，宏观时空尺度的不同拟序结构间的动量交换并不像分子间动量交换那么迅速，不能在当时当地迅速完成，其弛豫时间是宏观尺度，不能忽略不计，同时拟序结构具有一定的空间尺度和体积，从而，表现为雷诺应力与拟序结构运动变形之间在时空上的不同步性，即它们之间存在着时空相位差。平衡态下各向同性的涡粘系数形式对雷诺应力的行为施加了一些严格的而且有可能是非物理的限制。首先，标量的涡粘系数使得应力张量的主轴与相干结构应变率张量的主轴相一致，或者是Liu［9］所提出的线性化问题，应力与应变率的相位锁定。Jia［10］采用热线技术研究了壁湍流中调制雷诺应力R12与拟序结构应变率S12的相位平均波形，发现两者之间存在时间上的相位差，并证实了涡粘系数是相位沿法向变化的复数。在许多非平衡非局部湍流场中，由于湍流涡结构的运动的弛豫效应，涡粘系数中包含相位信息这一现象也是非常显著的。这种现象具有一定的物理意义，在湍流动量交换过程中，湍涡运动的时间和空间尺度，与分子运动相比，需要考虑，因为湍涡的变形在时间和空间上不会与雷诺应力相一致。因此，在非平衡湍流中，时空弛豫效应不能忽略不计。

国内钾肥继续呈现居高走势，进口钾货源紧张价格且高，近期将有大批氯化钾补充国内市场，内销交投短线延续紧张形势。硫酸钾在成本和库存压力的支撑下价格回落可能性很小，预计价格稳定、交投冷清的局面短期内还会继续。

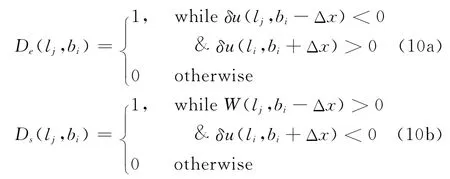
应用空间条件相位平均技术来获得第j尺度拟序结构低速区喷射和高速区扫掠的相位平均成分〈f（lj，x）〉：

其中Nj是第j尺度拟序结构喷射或者扫掠事件的个数，bi是喷射或者扫掠发生的位置，lj是第j尺度拟序结构猝发的流向空间尺度。

3 实验结果与分析

将原始速度场进行空间局部平均的多尺度结构分析，获得4个尺度的空间局部平均多尺度结构函数，选取满足条件（10）的空间位置，并以这一位置为中心切出尺寸为33×33×9（个数据点）的长方体，将所有满足条件的长方体内的湍流物理量进行空间相位叠加并做平均，获得拟序结构喷射、扫掠事件的空间相位平均拓扑，从而，从瞬时速度场中提取出拟序结构低速区喷射和高速区扫掠的相位平均特征量：相位平均的速度分量、涡量分量、调制雷诺应力分量和拟序结构速度应变率分量。根据小波分析检测拟序结构的能量最大准则，对能量最大尺度为第四尺度的拟序结构进行分析，其中，第四尺度所对应空间网格数为24个，相应的粘性壁面单元为240个，相应的空间长度约为10.992mm（以下图中，坐标X是流向方向，Y是展向方向，Z是法向方向）。图3给出法向位置z＋＝71处流向－展向平面内拟序结构猝发过程中相位平均速度的等值面图：（a）流向速度；（b）展向速度；（c）法向速度。从图中看到，在喷射过程中，流向速度在喷射中心存在低速区，低速区周围被流向速度的高速区流体包裹，低速流体的法向速度向上远离壁面，周围高速流体的法向速度向下冲向壁面，在喷射中心区域周围分布着展向速度的两个极大值区域和极小值区域。扫掠过程中，3个速度分量的分布情况与喷射过程正好相反。在靠近喷射中心区域的下游位置，速度矢量的方向呈现向四周发散的状态，而在扫掠中心区域的下游，速度矢量的方向呈现由四周向中心汇聚的状态，低动量流体和上游高速流体相遇而形成滞留点。

图4给出拟序结构猝发过程中展向中心截面流向速度和展向涡量的等值面分布。在喷射过程中，低速流体向斜后方喷射，符合流向脉动速度为负，法向脉动速度为正的喷射机理。在扫掠过程中，高速流体向斜前方冲向壁面，带动周围的低速流体使其加速。从涡量等值面图中看出喷射和扫掠事件中依然存在反向旋转的展向涡结构，但是涡量值相互异号。

图3 在法向位置y＋＝71，X－Y平面内喷射（上）和扫掠（下）过程中空间相位平均速度的等值面图Fig.3 Spatial phase averaging velocity contour during ejection and sweep at y＋ ＝71in streamwise－span plan

图4 拟序结构猝发过程中X－Z截面流向速度U和展向涡量W2的空间相位平均分布等值面图Fig.4 Spatial phase averaging distribution of the flow around the ejection and sweep event for CS in the streamwise－wall－normal plane

图5给出拟序结构猝发过程中Y－Z截面流向速度和流向涡量的等值面分布。在喷射事件中，在喷射中心，低速流体受到两个反向旋转的流向涡的作用而向远离壁面的方向运动，在低速流体两侧是高速流体，从相干结构的形态特征分析，可以看出在发卡涡的两涡腿的中间低速流体向外喷射。在扫掠事件中，高速流体向下扫掠，而在扫掠中心两侧分布着低速流体。喷射事件和扫掠事件中均存在反向旋转的流向涡结构，而涡量值相互异号。

综而言之，康、乾二帝对江南景观的选择与写仿，满足了他们放松身心、漫游胜境的需求以及将天下名园胜景归为己有的愿望，对江南景观产生了重要影响。从宏观角度来说，康、乾二帝与江南景观之间的互动，也促进了满汉之间、南方与北方、宫廷与江南的文化艺术交流，实现了清王朝从地理格局大一统向政治文化格局大一统的转变。

图7给出拟序结构扫掠过程中应变率分量与调制雷诺应力分量的空间相位平均分布等值面图。对比喷射和扫掠过程中S11，S22，S33的空间分布，在喷射过程中，应变极大值对应的位置正好是扫掠过程中应变极小值对应的位置；喷射和扫掠过程中，调制雷诺应力分量R11，R22，R33的极大值均分布在近壁区域，说明拟序结构猝发过程中，无论是喷射还是扫掠过程，随机脉动均在近壁区域活动最为活跃。对比调制雷诺应力和拟序结构速度应变的空间分布，两者对应各个分量的极值分布不一致，且空间相位不同步性也与拟序结构猝发的具体物理过程相关。

图5 拟序结构猝发过程中Y－Z截面流向速度U和流向涡量W1的空间相位平均分布等值面图Fig.5 Spatial phase averaging distribution of the flow around the ejection and sweep event for CS in the span－wall－normal plane

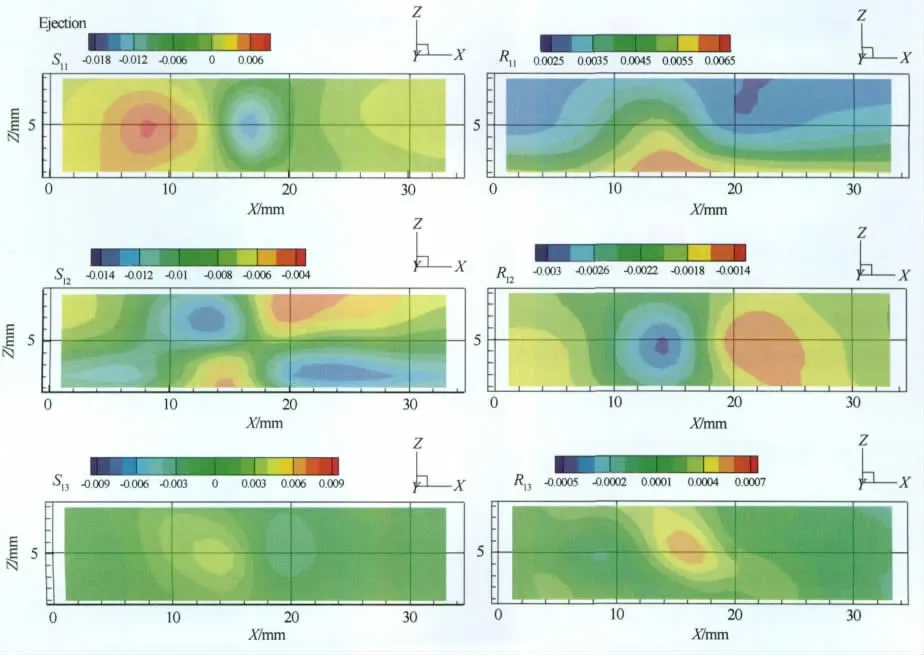
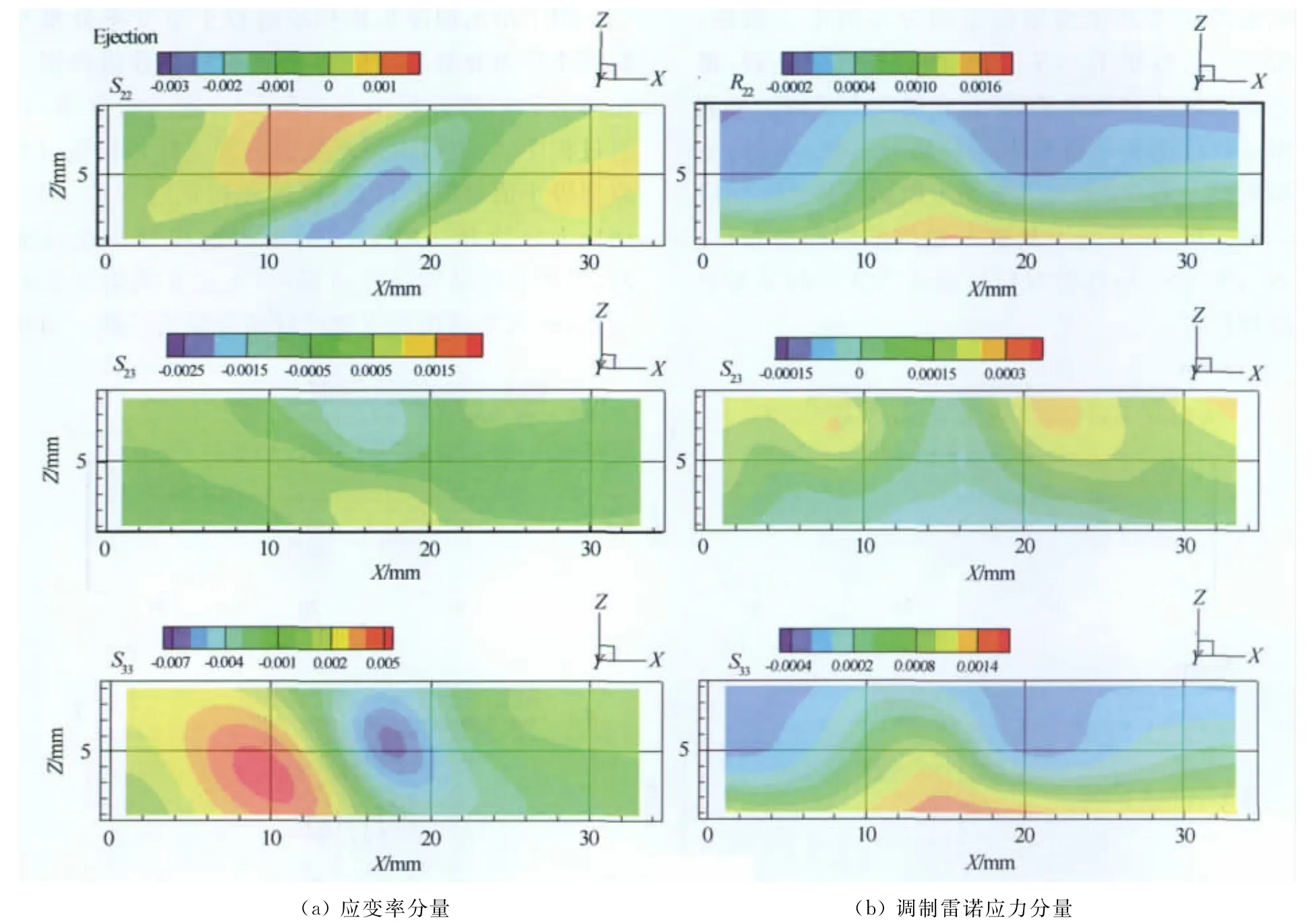
图6 X－Z平面内拟序结构喷射过程中应变率分量与调制雷诺应力分量的空间相位平均分布等值面图Fig.6 Spatial phase average of CS rate－of－strain components and modulated Reynolds stress components for CS during the ejection process in streamwise－wall－normal plan

图7 X－Z平面内拟序结构扫掠过程中应变率分量与调制雷诺应力分量的空间相位平均分布等值面图Fig.7 Phase averaging distributions of CS rate－of－strain components and modulated Reynolds stress components for CS during the sweep process in the streamwise－wall－normal plan

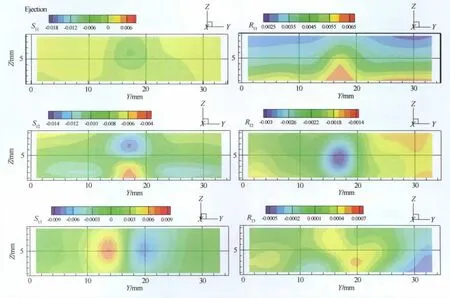
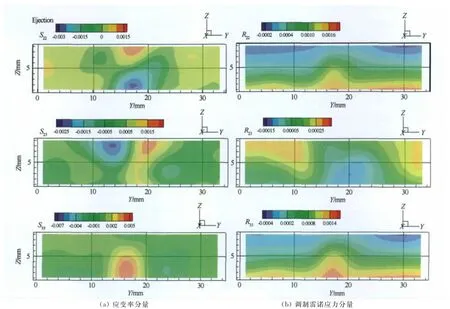
图8 Y－Z平面内拟序结构喷射过程中应变率分量与调制雷诺应力分量的空间相位平均分布等值面图Fig.8 Spatial phase averaging distributions of CS rate－of－strain components and modulated Reynolds stress components for CS during the ejection process in the span－wall－normal plan

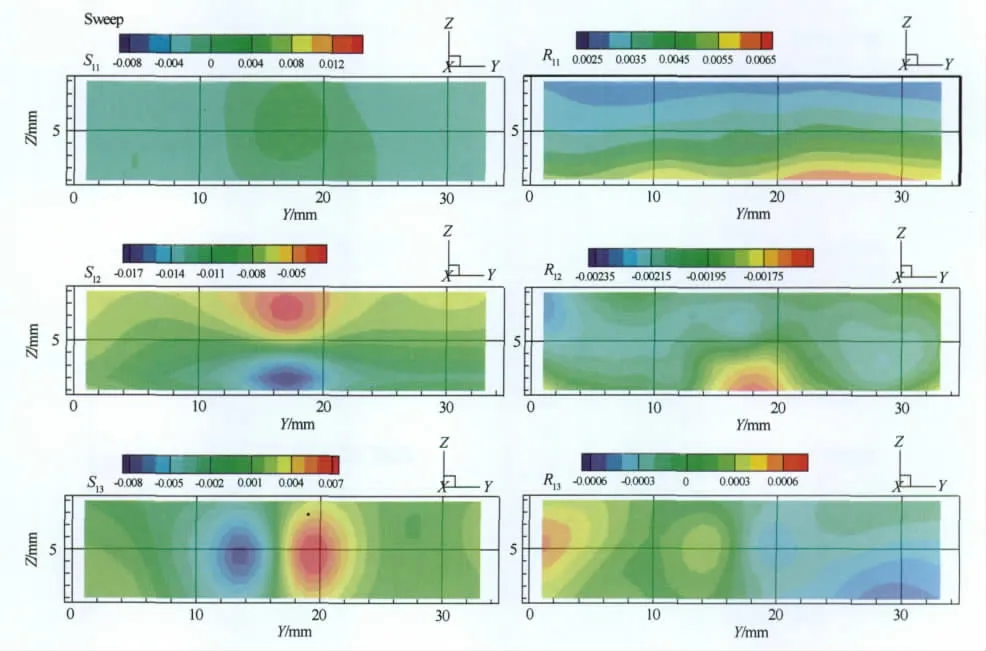
图9 Y－Z平面内拟序结构扫掠过程中应变率分量与调制雷诺应力分量的空间相位平均分布等值面图Fig.9 Spatial phase averaging distributions of CS rate－of－strain components and modulated Reynolds stress components for CS during the sweep process in the span－wall－normal plan

图8给出Y－Z平面内拟序结构喷射过程中应变率分量与调制雷诺应力分量的空间相位平均分布等值面图。可以看到，拟序结构应变率极值大概分布在喷射和扫掠的中心区域，分量S12，S22的极大值与极小值沿着切面的法向方向分布，位于切面流向中心；S13，S23的极大值与极小值沿着切面的流向方向分布。调制雷诺应力分量R11，R22，R33的幅值在壁面附近最大，随着远离壁面，幅值逐渐变小，R11的幅值由0.0065 降到0.0025，R22的幅值由0.0016 降到0.0002，R33的幅值由0.0014降到0.0001，这种变化趋势说明近壁区随机脉动对拟序结构贡献的雷诺应力最大。图9给出Y－Z平面内拟序结构扫掠过程中应变率分量与调制雷诺应力分量的空间相位平均分布等值面图。调制雷诺应力R11，R22，R33在近壁区幅值依然最大，随着远离壁面逐渐减小。对比图8与图9，在喷射阶段，S12，S13，S22，S23，S33的极大值位置正好对应于扫掠阶段极小值的位置。

4 结 论

应用层析PIV技术测量了壁湍流中三维测量体内的速度场，研究了调制雷诺应力分量和拟序结构应变率分量在拟序结构猝发过程中的空间相位平均分布形态，主要结论如下：

（1）拟序结构应变率6个分量与对应的调制雷诺应力6个分量的空间分布不一致，两者之间具有空间相位的不同步性。调制雷诺应力张量与拟序结构应变率张量之间的时空相位不一致性与拟序结构猝发的具体物理过程（喷射，扫掠）有关。调制雷诺应力与应变之间空间相位分布的不同步性说明壁湍流中大尺度拟序涡结构之间相互作用而引起动量传递的时空弛豫效应不能忽略不计，这是目前用于非平衡湍流场中的湍流模式理论需要考虑的一个重要因素。

（2）应用经典的线性Boussinesq涡模型不能准确地描述非平衡湍流的物理机理。应考虑调制雷诺应力张量与拟序结构应变率张量之间的时空相位不同步性，采用包含时空相位信息的复涡粘张量模型对调制雷诺应力进行模拟，从而两者的时空相位保持一致，得到正确的调制雷诺应力分布。这一现象在工业领域中的非平衡湍流场也普遍存在，比如叶轮机械的湍流计算。目前工业领域广泛应用的线性k－ε模型具有一定的缺陷，在对三维非平衡湍流进行数值模拟计算时，应考虑应力张量与速度变形率张量之间的时空弛豫效应，用包含时空相位信息的复涡粘张量模型来模拟雷诺应力张量是合理的，这一模型有可能成为一个很有发展前景的封闭模型，从而更加精准地预测工业领域中广泛存在的非平衡湍流。

致谢：德国国家航空中心空气动力与流动技术研究所为本文工作提供了实验数据，特此致谢。

［1］ADRIAN R J.Closing in on models of wall turbulence［J］.Science，2010，329：155－156.

［2］REYNOLDS W C，HUSSAIN A K M F.The mechanics of an organized wave in turbulent shear flow.Part 3［J］.J.Fluid Mech.1972，54：263－288.

［3］LUMLEY J L.Toward a turbulent constitutive relation［J］.J.Fluid Mech.，1970，41：413－434.

［4］POJE A C，LUMLEY J L.A model for large－scale structures in turbulent shear flows［J］.J.Fluid Mech.，1995，285：349－369.

［5］YU D，GIRIMAJI S S.Direct numerical simulations of homogeneous turbulence subject to periodic shear［J］.J.Fluid Mech.，2006，566：117－151.

［6］HADZIC I，HANJALIC K，LAURENCE D.Modeling the response of turbulence subjected to cyclic irrotational strain［J］.Phys.Fluids，2001，13（6）：1740－1747.

［7］BARDINA J.Improved turbulence models based on large eddy simulation of homogeneous，incompressible，turbulent flows［D］.Stanford University，1983.

［8］CHEN J，MENEVEAU C，and KATZ J.Scale interactions of turbulence subjected to a straining－relaxation－destraining cycle［J］.J.Fluid Mech.，2006，562：123－150.

［9］LIU J T C.Contributions to the understanding of largescale coherent structures in developing free turbulent shear flows［J］.Adu.Appl.Mech.，1988，26，183－309.

［10］JIA Y X，TANG Z Q，JIANG N.Experimental investigation of Reynolds stress complex eddy viscosity model for coherent structure dynamics［J］.Science in China Series G－Physics Mechanics ＆ Astronomy，2011，54（7）：1319－1327.

［11］ELSINGA G E，WESTERWEEL J.Tomographic－PIV measurement of the flow around a zigzag boundary layer trip［C］／／Proceedings of 15th international symposium on applications of laser techniques to fluid Mechanics，Lisbon，Portugal，05－08July，2010.

［12］SCHLATTER P.Vortical and large－scale structures in a turbulent boundary layer［R］.Poster，Linne Flow Centre，KTH Mechanics，Stockholm，Sweden，2010.

［13］ELSINGA G E，SCARANO F，et al.Tomographic particle image velocimetry［J］.Experiments in Fluids，2006，41：933－947.

［14］JIANG N，LIU W，et al.Phase－averaged waveforms of Reynolds stress in wall turbulence during the burst events of coherent structures［J］.Science in China Series G－Physics Mechanics ＆ Astronomy，2008，51（7）：857－866.